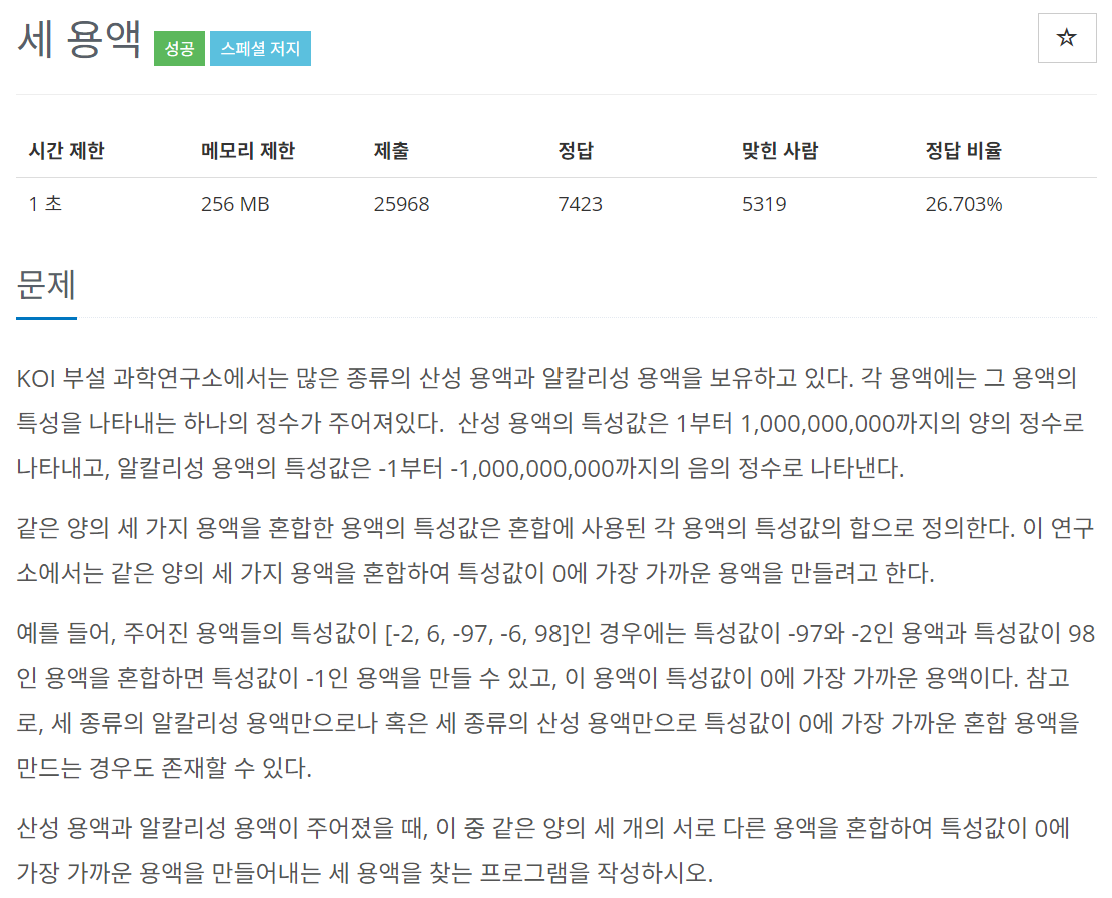

문제 해석
백준 2467번 : 용액 문제와 딱 하나만 다른 문제였다. 용액 문제에 관한 설명은 앞의 링크를 참조!
기존 용액 문제는 여러 용액들 중 두 용액의 특성값의 합이 0에 가장 가까운 두 용액을 뽑는 문제였다면, 이번에는 그러한 용액을 세 개를 뽑는 문제다.
뭐가 필요할까
투 포인터를 사용한 용액 문제에서 한 용액을 더 뽑아야 하니, 하나의 포인터를 추가하여 세 포인터로 문제를 해결하면 좋을 것 같다!
시행착오
그래서 처음에는 일단 용액 코드를 긁어와서, 대충 포인터를 하나 추가해서 바꿔주었다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;
int N;
vector<int> v;
int main() {
cin >> N;
v.resize(N); // N 크기로 벡터 초기화
for (int i = 0; i < N; i++)
{
cin >> v[i]; // 벡터에 용액의 특성값 입력
}
sort(v.begin(), v.end()); // 오름차순 정렬
int left = 0; // 포인터의 초기값 세팅
int mid = left + 1;
int right = N - 1;
int tuple_left = v[left];
int tuple_mid = v[mid];
int tuple_right = v[right];
int minVal = abs(v[left] + v[mid] + v[right]);
// 특성값 합의 절대값의 최소값을 저장할 변수 minVal
while (left < mid && mid < right) { // left, mid, right 교차될 때 까지
int val = v[left] + v[mid] + v[right]; // 세 특성값의 합
if (minVal > abs(val)) { // 혼합 특성값의 최소값 갱신
minVal = abs(val);
tuple_left = v[left];
tuple_mid = v[mid];
tuple_right = v[right];
}
if (val < 0) {
left++;
// 음수가 더 커서 혼합 특성값이 음수
// 절대값을 낮추기 위해 음수의 절대값을 낮추는데...
// 요기서 그럼 mid는 어떻게 되는거?
}
else {
right--;
}
}
cout << tuple_left << " " << tuple_mid << " " << tuple_right << "\n";
return 0;
}용액의 갯수와 특성값을 입력받고, 특성값 벡터를 정렬한다.
이후 세 포인터 left, mid, right을 위와 같이 정의하고, 용액 문제에서 했던 것 처럼 혼합 특성값이 음수라면 left를 땡겨와 음수 부분의 절대값을 줄이고, 혼합 특성값이 양수라면 right를 땡겨와 양수 부분의 절대값을 줄인다.
그런데 여기서 대체 mid가 어떻게 움직여야 할 지 감이 오지를 않아서 그냥 시원하게 백준에 제출하고 시원하게 2%에서 틀렸다.
그래서 어떻게 했는데
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll; // int 대신 long long 사용
ll N;
ll minVal = 3000000001; // minVal의 최초값 정의
vector<ll> v;
int main() {
cin >> N;
v.resize(N); // N 크기로 벡터 초기화
for (int i = 0; i < N; i++)
{
cin >> v[i]; // 벡터에 용액의 특성값 입력
}
sort(v.begin(), v.end()); // 오름차순 정렬
ll left = 0; // 포인터의 초기값 세팅
ll mid = left + 1;
ll right = N - 1;
ll tuple_left = v[left];
ll tuple_mid = v[mid];
ll tuple_right = v[right];
for (int i = 0; i < N - 2; i++)
{
left = i;
mid = left + 1;
right = N - 1;
// 하나의 for 루프에서 left는 고정, mid, right만 움직인다!
while (mid < right) {
ll val = v[left] + v[mid] + v[right];
if (minVal > abs(val)) { // 혼합 특성값의 최소값 갱신
minVal = abs(val);
tuple_left = v[left];
tuple_mid = v[mid];
tuple_right = v[right];
}
// left가 고정이니까 떼어버리고 투 포인터로 생각
if (val < 0) {
mid++;
// 음수가 더 커서 혼합 특성값이 음수
// 절대값을 낮추기 위해 음수의 절대값을 낮추기 -> mid를 당겨옴
}
else {
right--;
// 양수면 반대로 right을 당겨옴
}
}
}
cout << tuple_left << " " << tuple_mid << " " << tuple_right << "\n";
return 0;
}우선 int 대신 long long을 사용한 이유로는,
세 용액의 특성값이 모두 10억일 경우엔 혼합 특성값이 30억이 되는데 이 때 int의 범위를 벗어나기 때문이다.
따라서 특성값 합의 절대값의 최소값을 저장할 변수 minVal은 3000000001 로 설정하였다.
수정한 코드에서 가장 중요한 부분이 바로 for 문이라고 볼 수 있는데, 한 루프에서 left 포인터를 고정시켜놓고, mid와 right만으로 투 포인터 탐색을 진행한다.
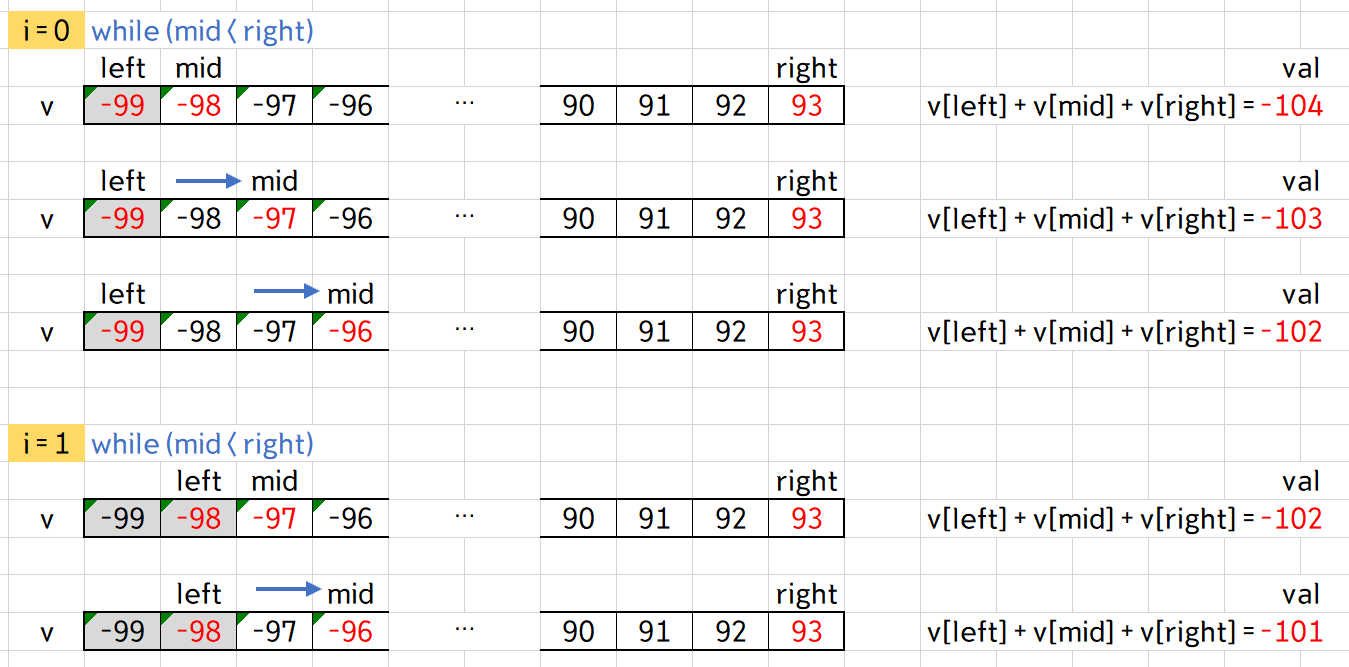
위의 사진에서 볼 수 있듯, left를 고정시키고 mid와 right만 이동하였다. 결국 for 루프를 다 돌면 가능한 세 가지 용액 조합을 다 만들어볼 수 있고, 최종적으로 minVal에는 최소값이 저장된다.
그 때의 left, mid, right에 위치한 용액의 특성값은 모두 tuple_left, tuple_mid, tuple_right에 저장되고, 이를 출력한 것이 답이 된다.
반례는 여기서 확인하면 될 것 같다!
