[백준/JAVA] 기본 수학2 - 1929번 소수구하기

더 좋은 문제 풀이가 있거나 궁금하신 점이 있다면 편하게 댓글 남겨주세요!

📝 문제

---

1929번 소수구하기

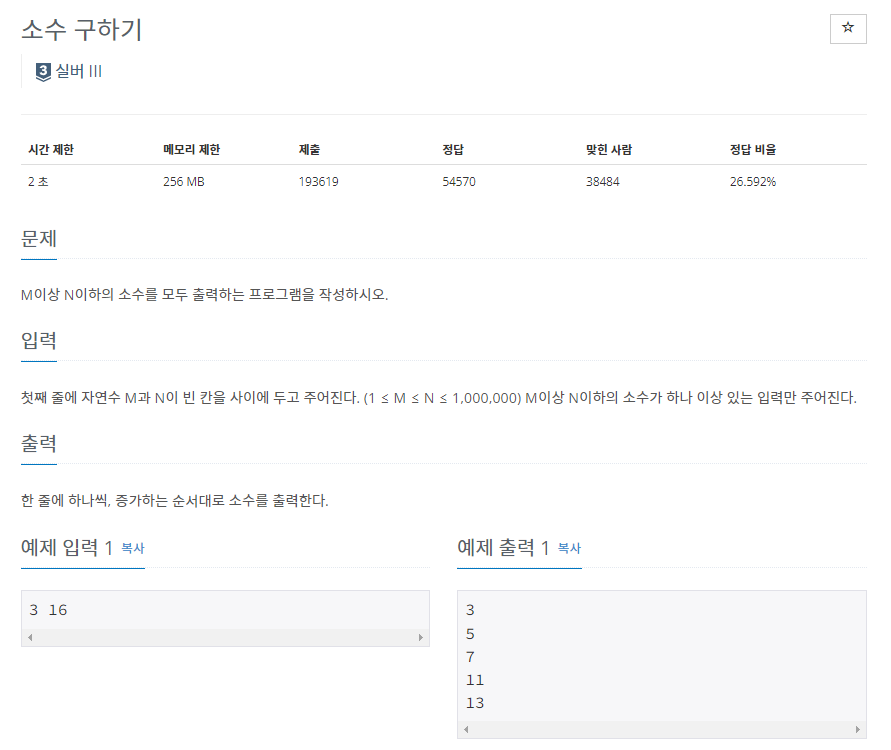
🤷‍♂️ 접근 방법

---

저는 처음 문제를 풀 때, 시간 제한이 있는 줄 모르고 2부터 해당 수까지 전부 반복하다 시간 초과가 발생하였습니다.
아래의 방법의 두가지 방법을 통해 시간 복잡도를 줄이며 문제를 풀어보겠습니다.

📌 N이 소수인지 판별 - 시간복잡도 O(√N)

먼저 시간복잡도가 O(√N)인 방법으로 숫자 N이 소수인지를 판별해 보겠습니다.

    for (int j = 2; j <= Math.sqrt(i); j++) {
        if (i % j == 0) {
            check = true;
            break;
        }

    }

예를 들어 숫자 20까지의 소수를 판별한다고 하면 √20 =4.47213xx 이고, 20 의 약수는 (1,20), (2,10), (4,5), (5,4), (10,2), (20,1) 입니다.

이 원리를 이용하여 N이 2에서 부터 √N 까지 나누어 떨어지는지 확인하며 소수인지 판별할 수 있습니다.

📌 N 이하의 모든 수 소수 판별(에라토스테네스의 체) - 시간복잡도 O(Nlog(log N))

또 다른 방법으로는 여러 수를 소수인지 아닌지 판별하는 에라토스테네스의 체가 있습니다.
에라토스테네스의 체는 N 이하의 모든 소수를 판별하는 알고리즘으로, N의 루트를 씌운 값의 배수까지만 확인하면 되는 방법입니다.

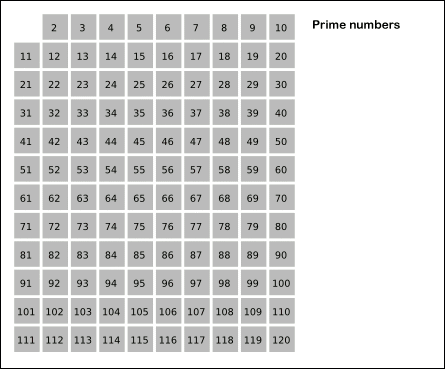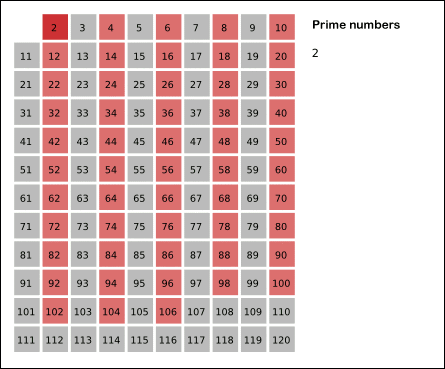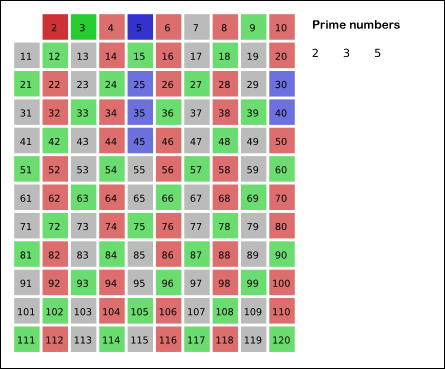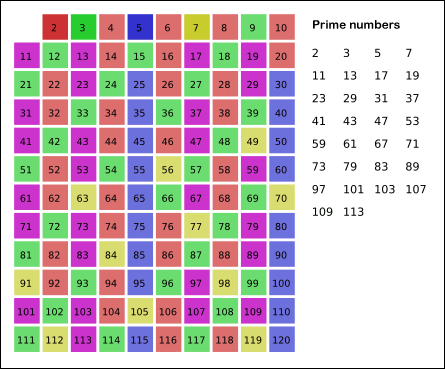
위의 그림에서 알 수 있듯이 알고리즘은 다음과 같습니다.

1. 2부터 N까지의 모든 자연수를 나열한다.
2. 아직 처리하지 않은 가장 작은 수 i를 찾고 i의 배수를 제거한다.
3. i가 √N까지 2번의 과정을 반복한다.
4. 위 과정을 통해 남겨진 값들은 소수이다.

에라토스테네스의 체
소수 구하는 알고리즘 - 에라토스테네스의 체

✍ 풀이

---

📌 √N 사용법 - 시간복잡도 O(√N)

//시간복잡도 O(√N)
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);

        int M = sc.nextInt();
        int N = sc.nextInt();

        for(int i =M; i <=N; i++){
            boolean check = false;

            if( i == 1 ) continue;
            else if( i == 2 ) System.out.println(2);
            else {
                for (int j = 2; j <= Math.sqrt(i); j++) {
                    if (i % j == 0) {
                        check = true;
                        break;
                    }

                }
                if (check == false) System.out.println(i);
            }
        }

    }
}

📌 에라토스테네스의 체 - 시간복잡도 O(Nlog(log N))

import java.util.Scanner;

public class test22 {
    
    public static boolean prime[];

    public static void main(String[] args) {
        
        Scanner sc  = new Scanner(System.in);
        
        int N = sc.nextInt();
        
        make_prime(N);
        
        for (int i = 0; i < prime.length; i++){
            if(prime[i] == false) System.out.println(prime[i]);
        }

    }
    
    // 소수면 false
    // 소수가 아니면 true
    public static void make_prime(int N ){
        
        prime = new boolean[N+1]; // 0 ~ N
        
        if( N < 2) return;
        
        prime[0] = true;
        prime[1] = true;
        
        
        for(int i = 2; i < Math.sqrt(N); i++){
            
            if(prime[i] == true) continue;
            
            for (int j = i * i; j< prime.length; j = j+i){
                
                prime[j] = true;
                
            }
            
        }
        
        
    }

}