백준 1074번 Z Class 3문제 (Python, Silver1)

문제 이해

아래는 n=3인 표이다.
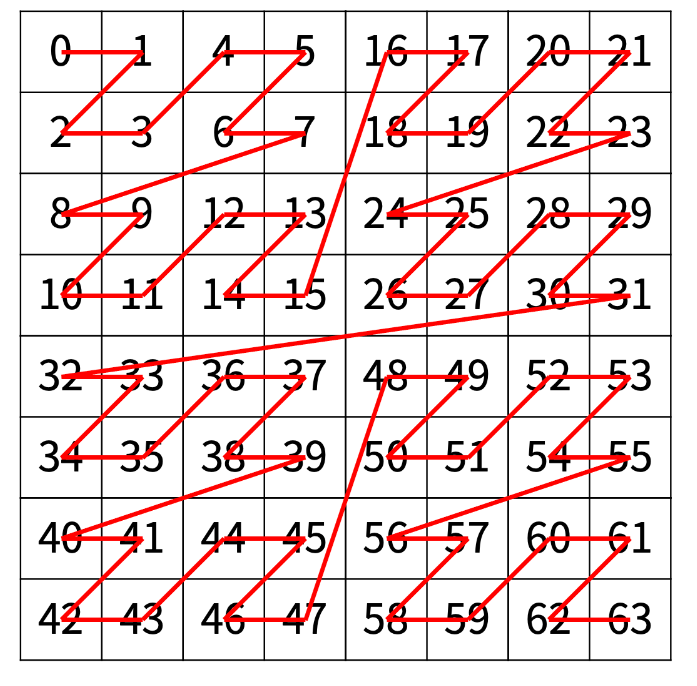
아래와 같이 Z모양으로 수가 증가하는 것을 알 수 있다. 0~7에 0~3이 0~3안에 0~1이 있다.
r, c를 입력받고 r행 c열에 있는 숫자를 출력하면 된다.

문제 접근

처음 풀이

처음에는 이 문제 그대로 배열을 생성하고 이를 재귀를 통해 숫자를 채워주는 방식으로 풀었는데 이렇게 되면 메모리와 시간을 많이 쓰게 되어 시간초과가 발생한다. 그래서 모든 부분을 재귀를 통해 구하면 시간이 많이 걸리는 것을 확인했다.

따라서 실제 구해야하는 위치를 제외한 부분은 길이의 제곱을 통해 수를 구해야겠다고 생각하였다.

import sys
N, r, c = map(int, sys.stdin.readline().split())
pan = [[0 for _ in range(2**(N))] for i in range(2**(N))]
# 0~2^N
# 0~2^N
temp = 0
def Z(n,x,y):
    global temp
    if n == 1:
        pan[x][y] = temp
        pan[x+1][y] = temp + 1
        pan[x+1][y] = temp + 2
        pan[x+1][y+1] = temp + 3
        temp+=4
        return
    else:
        Z(n-1,x, y)
        Z(n-1,x, y+(2**(n-1)))
        Z(n-1,x+(2**(n-1)), y)
        Z(n-1,x+(2**(n-1)), y+(2**(n-1)))
        return

Z(N, 0, 0)
print(pan[r][c])

새로운 방법

구하려는 위치가 재귀의 범위내에 존재하는지 확인한다.
범위내에 존재하지 않는다면 temp에 재귀의 범위의 크기만큼을 더해준다.
만약 범위내에 존재한다면 이를 재귀를 통해 또 범위를 나누어준다. 이때 순서는 Z가 진행되는 순서로 진행해야 한다.

따라서 실제로 배열을 생성하여 모든 재귀를 수행하여 값을 넣는 것이 아니라 temp라는 수를 통해 범위 내에 우리가 구하려는 값이 존재하지 않는다면 바로바로 값을 더해주는 것이다.

문제 풀이

def Z(n,x,y):
    global temp
    if x>r or x+(2**n)<=r or y>c or y+(2**n)<=c: # 재귀의 범위 내에 r,c가 없으면 temp에 그 넓이만큼 더해줌
        temp += (2**n)**2 # 길이의 제곱
        return # 부함수 종료
    if n == 1: # 2*2의 박스
        if x==r and y==c: # 1사분면
            print(temp)
        if x==r and y+1==c: # 2사분면
            print(temp+1)
        if x+1==r and y==c: # 3사분면
            print(temp+2)
        if x+1==r and y+1==c: # 4사분면
            print(temp+3)
        return # 종료
    else:
        n -= 1 # 4분의 1
        Z(n,x, y) # 1사분면
        Z(n,x, y+(2**n)) # 2사분면
        Z(n,x+(2**n), y) # 3사분면
        Z(n,x+(2**n), y+(2**n)) # 4사분면

제출 코드

import sys
N, r, c = map(int, sys.stdin.readline().split())
# 0~2^N
# 0~2^N
temp = 0
def Z(n,x,y):
    global temp
    if x>r or x+(2**n)<=r or y>c or y+(2**n)<=c: # 재귀의 범위 내에 r,c가 없으면 temp에 그 넓이만큼 더해줌
        temp += (2**n)**2 # 길이의 제곱
        return # 부함수 종료
    if n == 1: # 2*2의 박스
        if x==r and y==c: # 1사분면
            print(temp)
        if x==r and y+1==c: # 2사분면
            print(temp+1)
        if x+1==r and y==c: # 3사분면
            print(temp+2)
        if x+1==r and y+1==c: # 4사분면
            print(temp+3)
        return # 종료
    else:
        n -= 1 # 4분의 1
        Z(n,x, y) # 1사분면
        Z(n,x, y+(2**n)) # 2사분면
        Z(n,x+(2**n), y) # 3사분면
        Z(n,x+(2**n), y+(2**n)) # 4사분면
        
Z(N, 0, 0)