프로그래머스 미로 탈출 문제 풀이(Python, BFS, Lv2)

프로그래머스 미로 탈출 문제 바로가기

문제 접근

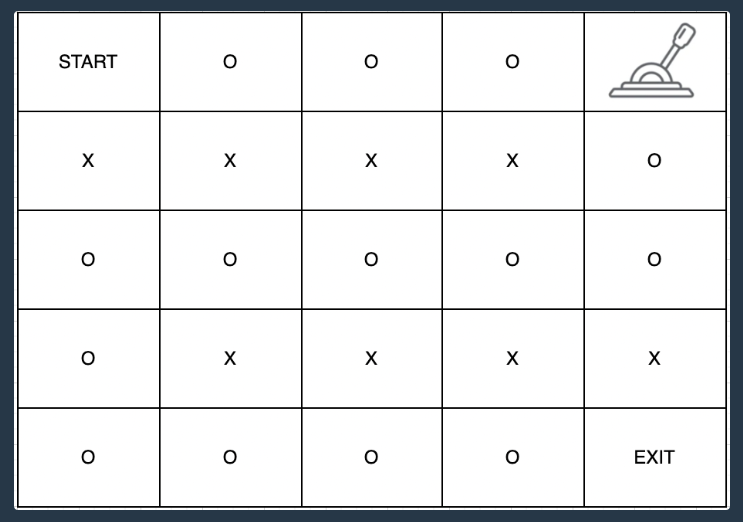
간단히 생각하면 start에서 레버를 당기러 갔다가 Exit로 가는 최소거리를 구하는 문제이다.
x로는 지나갈 수 없고 o로만 지나갈 수 있다.
이러한 표와 같은 좌표문제는 거의 무조건 BFS로 풀었었고, 최소거리를 구하는 문제이기 때문에 무조건 BFS이다. 라고 생각하고 풀었다.

따라서 start에서 레버까지의 최소거리 + 레버부터 Exit까지의 최소거리가 최종결과이다. 그렇다면 우리는 start를 시작으로 BFS한번 레버의 위치를 시작으로 BFS 한번을 돌려야 하느냐~ 는 아니다.
레버를 기준으로 BFS를 돌리면 start까지의 거리, Exit까지의 거리가 모두 나오기 때문이다.
따라서 두 값의 합을 구하면~ 정답이다.

문제 해결

시작, 레버, 종료 좌표 구하기

    N = len(maps)
    M = len(maps[0])
    visitedE = [[-1 for i in range(M)] for j in range(N)]
    for i in range(N):
        for j in range(M):
            if maps[i][j] == "S":
                sx = i
                sy = j
            if maps[i][j] == "L":
                lx = i
                ly = j
            if maps[i][j] == "E":
                ex = i
                ey = j

BFS함수

def bfs(a, b, visited):
        q = deque()
        q.append([a, b])
        visited[a][b] = 0
        while q:
            x,y = q.popleft()
            for i in range(4):
                nx = x + dx[i]
                ny = y + dy[i]
                if nx<0 or ny<0 or nx>=N or ny>=M or visited[nx][ny] != -1 or maps[nx][ny] == "X":
                    continue
                q.append([nx,ny])
                visited[nx][ny] = visited[x][y] + 1

결과 출력

두 거리 결과 중 하나라도 0보다 작은게 있다면 이어져있지 않다는 소리이므로 -1을 return한다.
그게 아니라면 두 값을 더한 값을 결과로 return한다.

    bfs(lx, ly, visitedE)
    
    if visitedE[ex][ey]<0 or visitedE[sx][sy]<0:
        return -1
    else:
        return visitedE[sx][sy] + visitedE[ex][ey]

제출 코드

from collections import deque
def solution(maps):
    answer = 0
    N = len(maps)
    M = len(maps[0])
    visitedE = [[-1 for i in range(M)] for j in range(N)]
    for i in range(N):
        for j in range(M):
            if maps[i][j] == "S":
                sx = i
                sy = j
            if maps[i][j] == "L":
                lx = i
                ly = j
            if maps[i][j] == "E":
                ex = i
                ey = j
                
    dx = [0,0,1,-1]
    dy = [1,-1,0,0]
    
    def bfs(a, b, visited):
        q = deque()
        q.append([a, b])
        visited[a][b] = 0
        while q:
            x,y = q.popleft()
            for i in range(4):
                nx = x + dx[i]
                ny = y + dy[i]
                if nx<0 or ny<0 or nx>=N or ny>=M or visited[nx][ny] != -1 or maps[nx][ny] == "X":
                    continue
                q.append([nx,ny])
                visited[nx][ny] = visited[x][y] + 1
                
    bfs(lx, ly, visitedE)
    
    if visitedE[ex][ey]<0 or visitedE[sx][sy]<0:
        return -1
    else:
        return visitedE[sx][sy] + visitedE[ex][ey]
# bfs로 최소시간 구하기