문제

https://www.acmicpc.net/problem/1463

풀이

먼저 이 문제는 다이나믹 프로그래밍을 이용해야 한다.
다이나믹 프로그래밍은 상향식과 하향식이 있는데 여기서는 상향식을 이용하였다.

문제에서 3가지의 방법을 줬다.

1. 3으로 나눠지면 3을 나눌 수 있다.
2. 2로 나눠지면 2로 나눌 수 있다.
3. 1을 뺄 수 있다.

문제에서는 수를 주고 이 수에서 1이 나올때까지 방법을 찾는 방식이지만,
상향식은 1에서 문제의 수까지 올라가는 방식이다.

여기서 DP라는게 등장한다. 사용방법을 알기 위해 그림을 참고해보자.

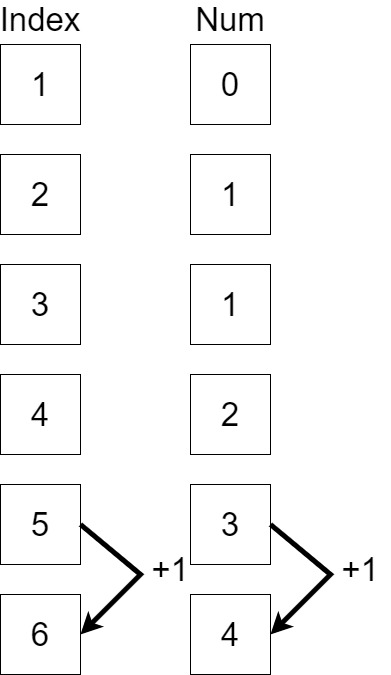
일단 기본적으로 수, 그러니까 1부터 입력받는 수까지 증가는 과정을 인덱스로 표현하고 그 값을 최소횟수로 사용할 것이다.
즉, 3을 입력받으면 Num[3]이 답이 되는 것이다.

제일 처음에 for문을 이용해서 로직을 돌린다고 가정하면 처음에 인덱스 값이 하나 증가할때, 인덱스의 Value값도 하나 증가시킨다. 이는 3가지의 방법 중 3. 1을 뺄 수 있다의 방법을 사용한다고 생각하면 된다. 그렇기 때문에 count를 하나 늘린 것이다.

예시를 보면 5에서 6으로 넘어갈때 5의 최소 카운터가 3이라면 6을 일단 4로 늘려놓는다.

그 후에 인덱스값 6이 2로 나눠지는지 확인한다. 나눠진다면 2로 나눈 인덱스 값의 Value에 +1을 하여 처음 4와 비교한다. 이는 3가지의 방법 중 2. 2로 나눠지면 2로 나눌 수 있다의 방법을 사용한 것이다.

마지막으로 인덱스값 6이 3으로 나눠지는지 확인한다. 나눠진다면 3으로 나눈 인덱스 값의 Value에 +1을 하여 바뀌어진 값 2와 비교한다. 이는 3가지의 방법 중 1. 3으로 나눠지면 3을 나눌 수 있다.의 방법을 사용한 것이다.

import java.util.Scanner;

public class Num1463 {

    public static int N;
    public static int Num[];

    public static void main(String[] args) {
        //input
        Scanner scanner = new Scanner(System.in);
        N = Integer.parseInt(scanner.nextLine());
        Num = new int[N + 1];

        //logic
        Num[1] = 0;
        for (int i=2; i<=N; i++) {
            Num[i] = Num[i-1] + 1;
            if (i % 2 == 0)
                Num[i] = Math.min(Num[i], Num[i/2] + 1);
            if (i % 3 == 0)
                Num[i] = Math.min(Num[i], Num[i/3] + 1);
        }

        //output
        System.out.println(Num[N]);
    }
}