기본적으로 알아둬야할 지식
고정 소수점 표현방식

부호비트 : 양수면 0 음수면 1
지수비트 : 정수부
가수비트 : 소수부
예시로 부동소수점에 대해 알아보자. 7.625 라는 실수가 있다고 하자 2진수로 바꾸면 111.101 가 될 것이다. 이를 위 그림에 넣으면 이렇게 된다.
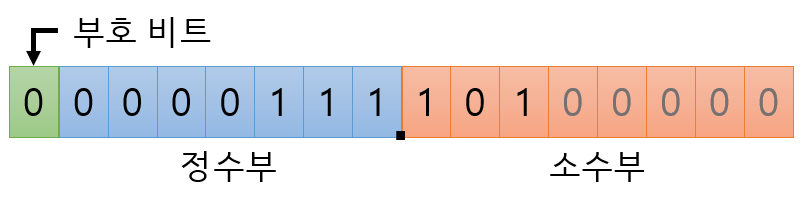
이게 고정소수점이다.
부동 소수점 표현방식
부동 소수점은 고정 소수점과 다르게 정규화 과정을 거친다.
정규화란 쉽게 말해 2진수를1.xx * 2^n 로 나타내는 것이다. 변환 방법은 소수점을 왼쪽으로 이동시킬때마다 n을 증가시키면 된다.
7.625->111.101->1.11101 * 2^2
이런 식이 된다. 이를 어떻게 표현하느냐.
부호비트는 똑같이 양수면 0 음수면 1로 넣는다. 소수부는 말 그대로 소수 부분 11101을 소수부의 첫번째부터 채워주면 된다. 나머지는 0으로 채운다. 정수부는 n에서 127을 더한 후 2진수로 변환한 값을 넣으면 된다. 예시에서 n은 2이므로 2+127=129를 2진수로 변환한. 10000001이 정수부가 된다. 다 완성한다면 이렇게 된다.

연산자(operator)
위키백과
위키백과에 보면 연산자에 대해 어떻게 처리해야하는지 나와있다. 자세한 내용은 뒤에서 설명하겠다.
ex00
고정 소수점을 나타내는 표준 클래스를 작성해라.
private:
고정소수점을 저장할 정수(int)
비트로 저장하기 위한 고정 상수(static const int). 항상 8.
public:
고정소수점을 0으로 저장할 생성자.
복사 생성자.
연산자.
int getRawBits( void ) const; 고정 소수점 반환.
void setRawBits( int const raw ); 고정 소수점 설정.
main
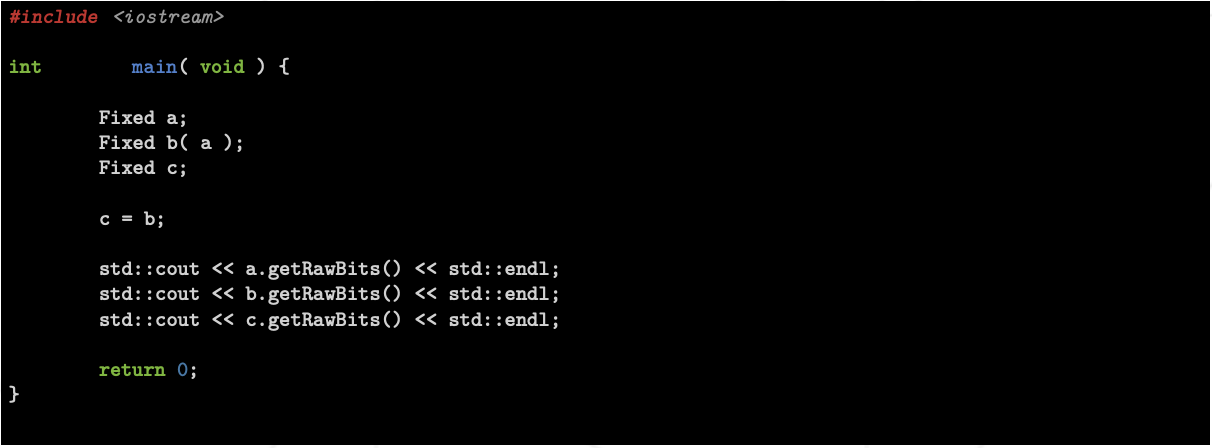
output
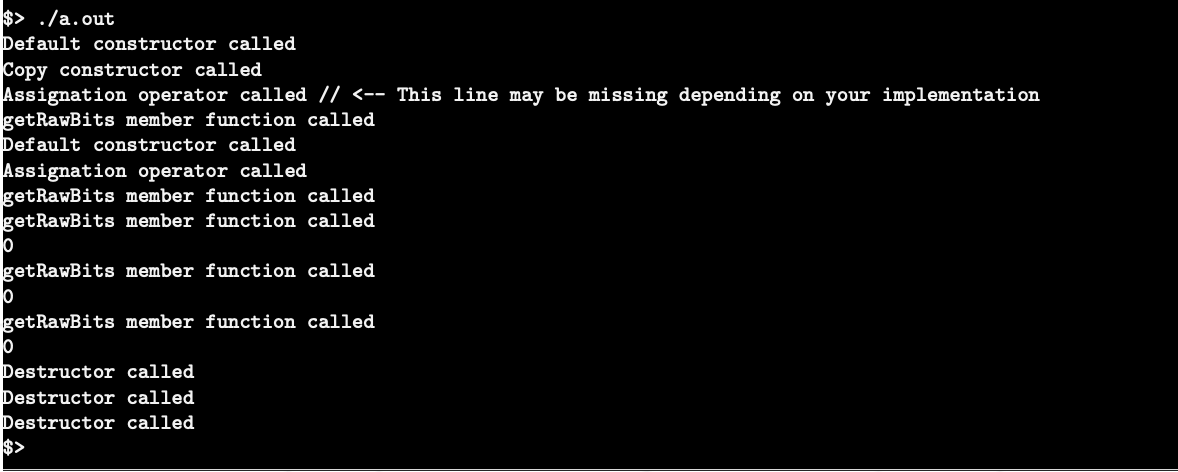
class Fixed
{
private:
int fix_value;
static const int frac_bit = 8;
public:
int getRawBits( void ) const;
void setRawBits( int const raw );
Fixed& operator=(const Fixed& fix);
Fixed();
~Fixed();
Fixed( const Fixed& fix);
};복사 생성자
Fixed::Fixed( const Fixed& fix) {
std::cout << "Copy constructor called" << std::endl;
*this = fix;
}fix를 this의 참조변수로 새로 저장한다.
연산자
Fixed& Fixed::operator=(const Fixed& fix) {
std::cout << "Assignation operator called" << std::endl;
this->setRawBits(fix.getRawBits());
return *this;
}위는 연산자의 사용방법이다. 위키백과에서 찾으면 형태가 나온다.

형태에 맞춰 사용하면 된다.
ex01
private:
고정소수점을 저장할 정수(int)
비트로 저장하기 위한 고정 상수(static const int). 항상 8.
public:
고정소수점을 0으로 저장할 생성자.
복사 생성자.
연산자.
int getRawBits( void ) const; 고정 소수점 반환.
void setRawBits( int const raw ); 고정 소수점 설정.
float toFloat( void ) const; 고정 소수점을 부동 소수점으로 변환.
int toInt( void ) const; 고정 소수점을 정수로 반환.
« 연산자에 대한 오버로드.(ostream)
main
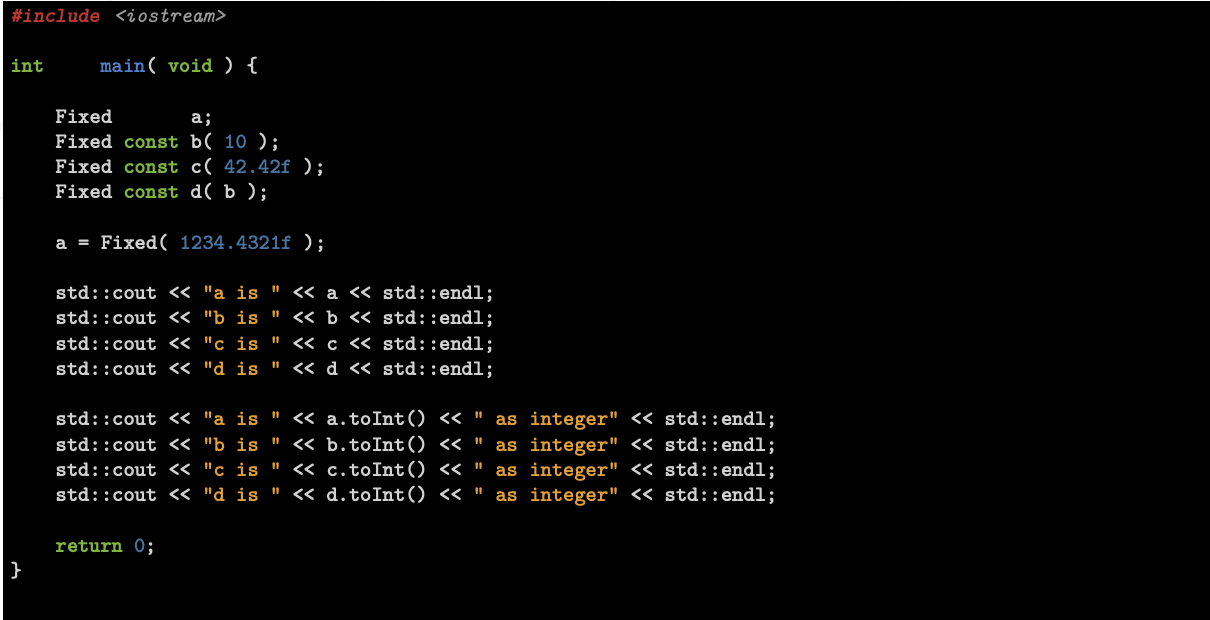
output
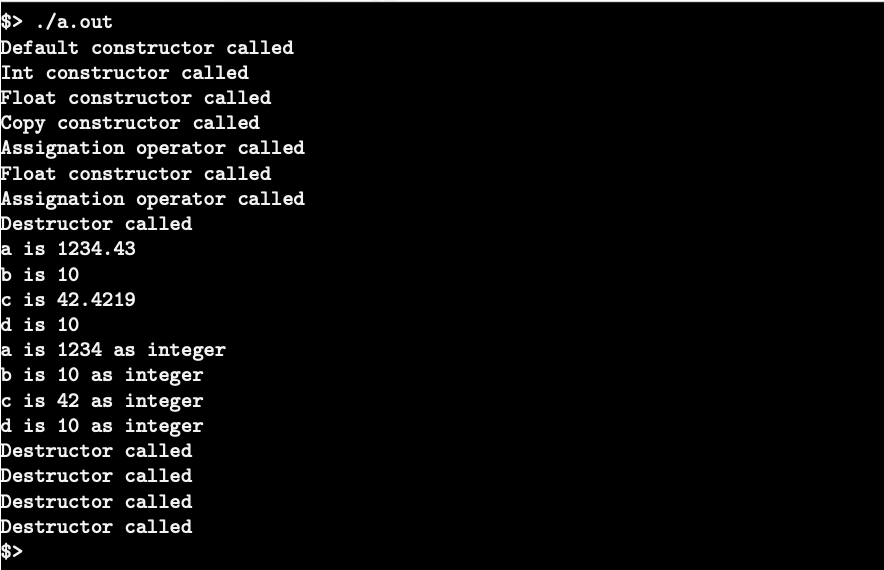
class Fixed
{
private:
int fix_value;
static const int frac_bit = 8;
public:
int getRawBits( void ) const;
void setRawBits( int const raw );
float toFloat( void ) const;
int toInt( void ) const;
Fixed& operator=(Fixed const &fix);
Fixed();
Fixed( const int r);
Fixed( const float f);
~Fixed();
Fixed( const Fixed& fix);
};
std::ostream& operator<<(std::ostream &out, const Fixed &fixed);정수를 고정소수점으로
2진수로 바꾼 값을 8비트의 공간으로 받아야 하기 때문에 쉬프트 연산자를 통해
n << 8
다음과 같이 된다.
고정소수점을 정수로
반대로
n >> 8
가 된다.
실수를 고정소수점으로
정수를 고정소수점으로 바꾼것과 동일하지만, float이나 double의 경우 직접적으로 쉬프트 연산자가 안된다. 그러므로 간접적으로 하기위해
f * (1 << 8)
이렇게 해준다. 또, 비교적 정확한 값을 만들기 위해 반올림을 해줘야한다.
여기서 허용함수인 roundf를 사용한다.
roundf(f * (1 << 8))
고정소수점을 실수로
위를 반대로 하면 된다.
(float)f / (1 << 8)
<< 오버로딩(커스텀 클래스)
main에서 어떻게 a 인스턴스 출력이 가능한걸까?
cout는 ostream의 객체이다. 그러므로 클래스를 cout로 출력하고 싶다면, ostram 클래스의 operator<<를 재정의하면 된다. operator<<를 메서드로 넣어도 되고 전역함수로 사용할 수도 있다. 여기서는 ostream의 소스코드를 건들지 않기위해 전역함수로 사용할 것이다.
ostream& operator<< (ostream &out, const Fixed &fixed) {
out << fixed.toFloat();
return out;
}ex02
public:
6가지 비교 연산자 : >, <, >=, <=, == , !=
4가지 산술 연산자 : +, -, *, /
전위증가, 후위증가, 전위감소, 후위감소 연산자
2개의 고정 소수점을 비교하여 작은 값을 반환하는 메서드
2개의 정적 고정 소수점을 비교하여 작은 값을 반환하는 정적 메서드
2개의 고정 소수점을 비교하여 큰 값을 반환하는 메서드
2개의 정적 고정 소수점을 비교하여 큰을 반환하는 정적 메서드
main
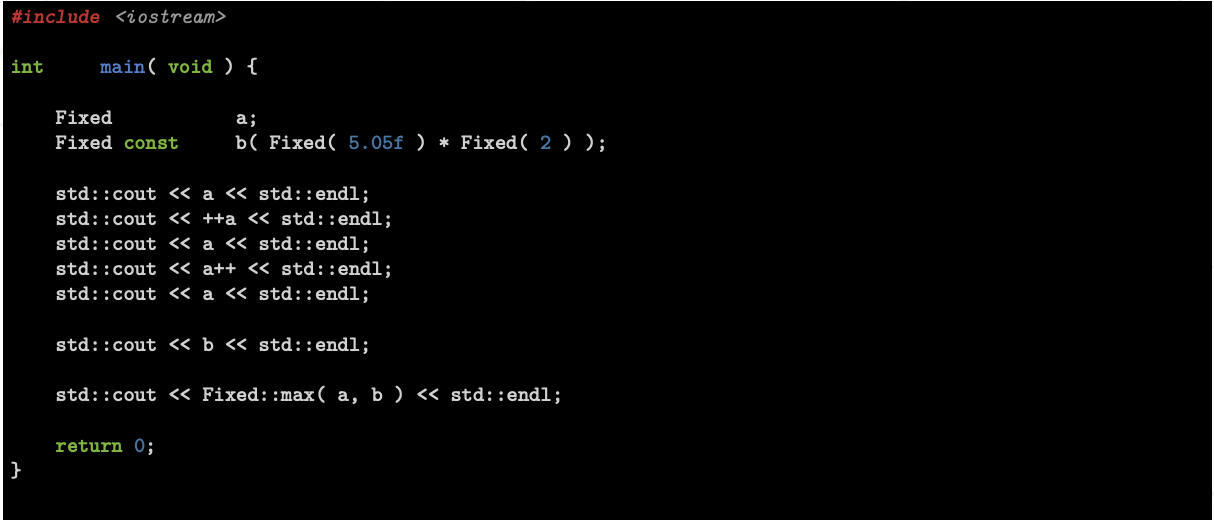
output
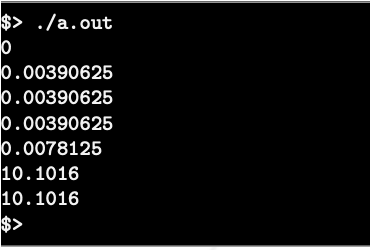
class Fixed
{
private:
int fix_value;
static const int frac_bit = 8;
public:
int getRawBits( void ) const;
void setRawBits( int const raw );
float toFloat( void ) const;
int toInt( void ) const;
Fixed& operator*(Fixed const &fix);
Fixed& operator/(Fixed const &fix);
Fixed& operator+(Fixed const &fix);
Fixed& operator-(Fixed const &fix);
bool operator>(Fixed const &fix) const;
bool operator<(Fixed const &fix) const;
bool operator>=(Fixed const &fix) const;
bool operator<=(Fixed const &fix) const;
bool operator==(Fixed const &fix) const;
bool operator!=(Fixed const &fix) const;
Fixed operator++(int);
Fixed& operator++();
Fixed operator--(int);
Fixed& operator--();
Fixed();
Fixed( const int r);
Fixed( const float f);
~Fixed();
Fixed( const Fixed& fix);
static Fixed& max(Fixed &a, Fixed &b);
static Fixed const &max(Fixed const &a, Fixed const &b);
static Fixed& min(Fixed &a, Fixed &b);
static Fixed const &min(Fixed const &a, Fixed const &b);
};
std::ostream& operator<<(std::ostream &out, const Fixed &fixed);비교
bool Fixed::operator>(Fixed const &fix) const {
if (this->fix_value > fix.fix_value)
return true;
return false;
}전위 증가, 후위 증가, 전위 감소, 후위 감소
이 또한 위키백과에 나와있다.

전위증가의 경우 ++를 더한 후에 출력이 되므로,
Fixed& Fixed::operator++() {
this->fix_value++;
return *this;
}이렇게 하면 된다.
후위 증가의 경우 출력 이후에 ++이 되야 하므로
Fixed Fixed::operator++(int) {
Fixed a(*this);
this->fix_value++;
return a;
}이렇게 된다. this->fix_value++ 로 인해 값이 증가되었지만, 출력할때의 리턴은 a이므로 출력할때는 증가되지않는 값이 출력되지만 이후에 this에서 증가되어 a도 증가된 값을 가지게 된다.
min, max
Fixed& Fixed::max(Fixed &a, Fixed &b) {
if (a > b)
return a;
return b;
}
Fixed const &Fixed::max(Fixed const &a, Fixed const &b) {
if (a > b)
return a;
return b;
}연산자를 이용하여 해결하면 된다. const를 넣으면 좀 더 안정감있는 함수가 완성된다.
ex03
Fixed 클래스
위의 예제를 이용
Point 클래스
priavte:
Fixed const x;
Fixed const y;
그외 필요한것들
public:
x, y를 0으로 초기화하는 기본 생성자
소멸자
복사 생성자
x, y를 float으로 받아 값을 넣는 생성자
연산자
그외 필요한것들
bsq 함수
bool bsp( Point const a, Point const b, Point const c, Point const point);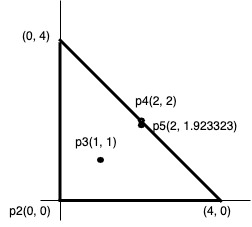
3개의 점을 받아 삼각형을 이루고, point가 삼각형 내부에 있으면 true 외부에있거나 삼각형의 가장자리에 있으면 false 반환하도록 하고 main에서 이를 테스트할 것.
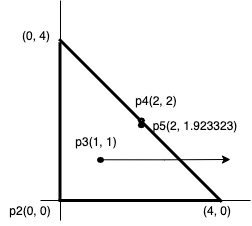
해결방법은 간단하다.
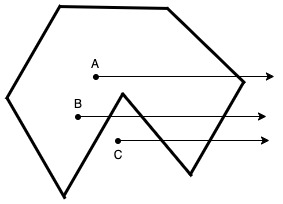
해결방법은 point를 x축의 한쪽방향으로 무지성으로 길이를 늘린 후에 선과 몇번 만났는지 카운트를 하면 된다. 위의 다각형을 보면 A는 한번 만나고 B는 3번 C는 2번 만난다. 그러므로 만난 횟수가 홀수면 도형의 내부에 있고, 짝수는 도형의 외부에 있게 된다. 이를 이용해서 bsp 함수를 만들면 된다.
int check_in(Point const l1, Point const l2, Point const p, bool *flag) {
Fixed a;
Fixed b;
Fixed new_p_x;
if (l1.get_y() - l2.get_y() == 0) {
if (p.get_y() == l1.get_y())
*flag = true;
return 0;
}
if (l1.get_x() - l2.get_x() == 0) {
if (p.get_x() < l1.get_x() && \
p.get_y() > Fixed::min(l1.get_y(), l2.get_y()) && \
p.get_y() < Fixed::max(l1.get_y(), l2.get_y()))
return 1;
else if (p.get_x() == l1.get_x() && \
p.get_y() >= Fixed::min(l1.get_y(), l2.get_y()) && \
p.get_y() <= Fixed::max(l1.get_y(), l2.get_y()))
*flag = true;
return 0;
}
a = (l1.get_y() - l2.get_y()) / (l1.get_x() - l2.get_x());
b = l1.get_y() - a * l1.get_x();
new_p_x = (p.get_y() - b) / a;
if (p.get_x() < new_p_x && \
p.get_y() > Fixed::min(l1.get_y(), l2.get_y()) && \
p.get_y() < Fixed::max(l1.get_y(), l2.get_y()))
return 1;
if (p.get_x() == new_p_x)
*flag = true;
return 0;
}
bool bsp( Point const a, Point const b, Point const c, Point const point) {
if ((a.get_x() == b.get_x() && b.get_x() == c.get_x()) || \
(a.get_y() == b.get_y() && b.get_y() == c.get_y()))
return false;
int count = 0;
bool flag = false;
count += check_in(a, b, point, &flag);
count += check_in(a, c, point, &flag);
count += check_in(b, c, point, &flag);
if (flag)
return false;
if (count % 2 == 1)
return true;
return false;
}위처럼 작성하였다. 쉽게 말하면 각 변을 하나의 함수로 보고, 기울기를 구하고 함수를 구해, point의 y좌표를 대입해서 조건에 맞는지 확인하는 알고리즘이라고 생각하면 된다.
.png)
