Container With Most Water

You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).

Find two lines that together with the x-axis form a container, such that the container contains the most water.

Return the maximum amount of water a container can store.

Notice that you may not slant the container.

Example 1:

Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7].
In this case, the max area of water (blue section) the container can contain is 49.

Example 2:

Input: height = [1,1]
Output: 1

Constraints:

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

Approach 1: Brute Force

In this case, we will simply consider the area for every possible pair of the lines and find out the maximum area out of those.

Note: Brute force 접근은 문제를 해결할때 직관적인 출발점이기에 해결방안으로 잘 포함되나 인터뷰때는 Time compelxity 제한으로 받아들여지지 않을 것이다.

public class Solution {
	public int maxArea(int[] height) {
    // 1. initialize max to Zero
    int maxarea = 0;
    // 2. A for loop for the left pointer
    for (int left = 0; left < height.length; left++) {
    	// 3. A for loop for the right pointer
    	for (int right = left+1; right < height.length; right++) {
			int width = right - left;
            // 4. Update maximum area
            maxarea = Math.ma(maxarea, Math.min(height[left], height[right]) * width);
            }
        }
        // 5. Return the maximum area
        return maxarea;
    }
}

Complexity Analysis

• Time complexity: O(n^2)
• Space complexity: O(1)

Approach 2: Two Pointer

이 접근법의 직관은 선이 항상 짧은 선의 길이로 제한되있다는 것이다. 또한 선이 멀 수록 더 많은 공간을 얻을 것이다.

2개의 포인터를 가져온다. 하나는 시작점에 있고 하나는 끝에 있다. 또한 우리는 지금까지의 최대넓이를 저장하기 위해 maxarea를 변수로 유지한다.

두 포인터 사이의 넓이를 구하고 maxarea를 업데이트 한다.
짧은 선을 가리키는 포인터를 다른쪽 으로 한 단계 이동한다.

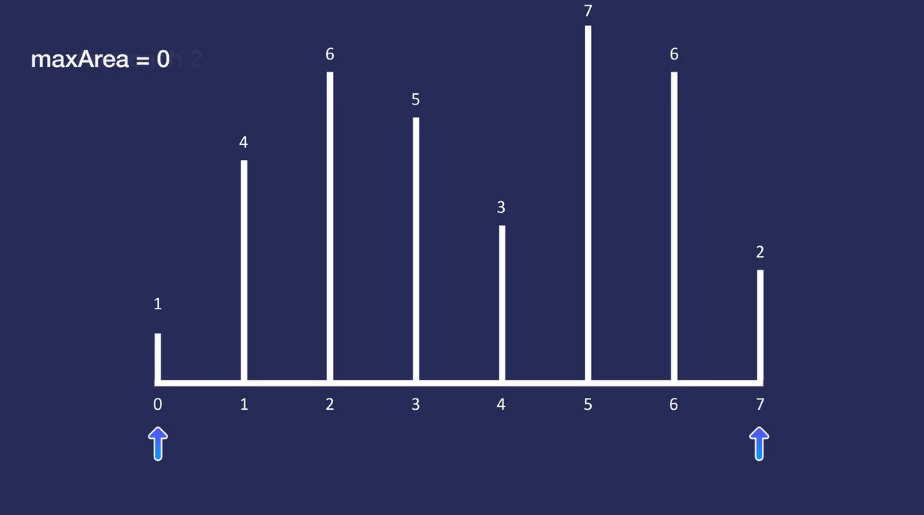
짧은 선을 이동하는 이유는 넓이가 짧은 선을 기준으로 정해지기 때문이다.

public class Solution {
    public int maxArea(int[] height) {
        // 1. Initialize max to zero
        int maxarea = 0;
        // 2. Initialize left and right to extreme ends of the array
        int left = 0; 
        int right = height.length - 1;
        // 3. while left > right, loop
        while (left < right) {
        	// 4. Calculate current area and update max area
            int width = right - left;
            maxarea = Math.max(maxarea, Math.min(height[left], height[right]) * width);
            // 5. Take decision regarding which pointer to move
            if (height[left] <= height[right]) {
                left++;
            } else {
                right--;
            }
        }
        // 6. return the maximum area
        return maxarea;
    }
}

Complexity Analysis

• Time complexity: O(n)
• Space complexity: O(1)