문제 링크 : https://programmers.co.kr/learn/courses/30/lessons/72413
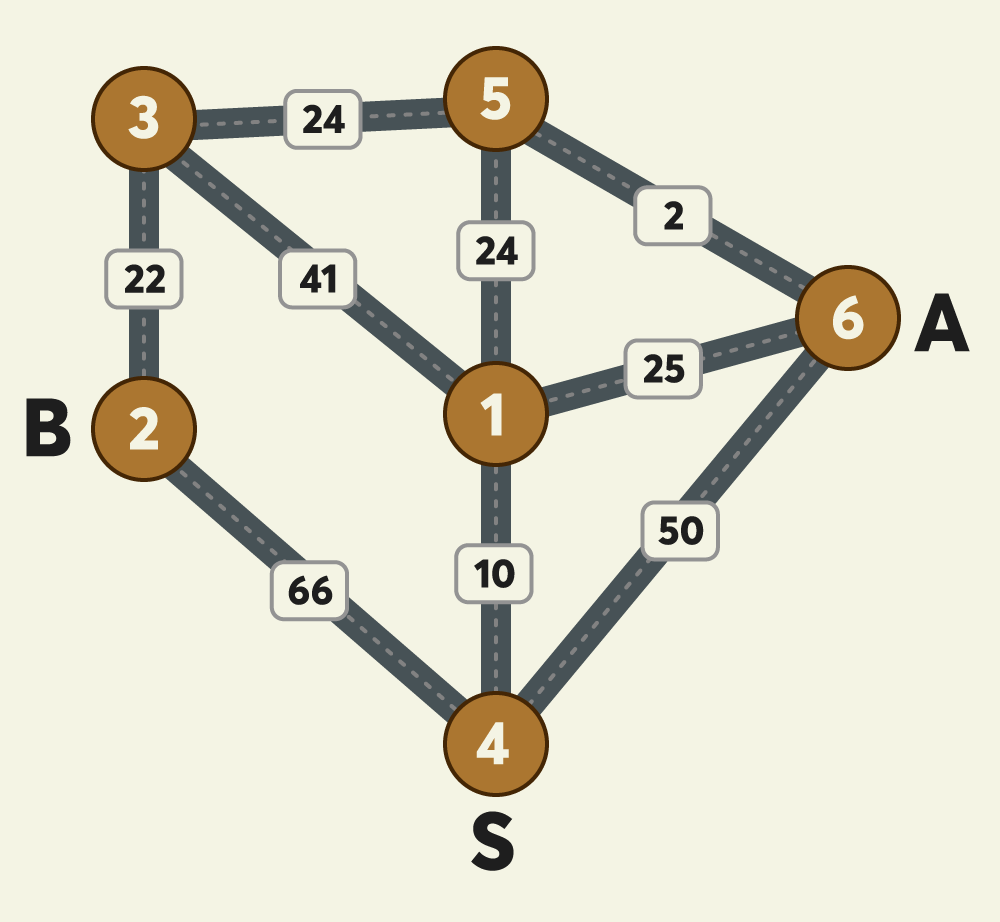
이 문제는 (S ➡ (어느 정점) ➡ A) + (S ➡ (어느 정점) ➡ B) 의 최소값을 찾는 문제였다.
최단 경로를 구하는 대표적인 알고리즘이 다익스트라 알고리즘인데, 음이 아닌 가중치 그래프일 때 특정 정점에서 다른 모든 정점으로 가는 최단 거리를 구할 때 주로 사용한다.
다익스트라 알고리즘 설명) https://m.blog.naver.com/ndb796/221234424646
이 문제는 하나의 정점이 아닌, 각 정점 간 최단 경로를 구하는 문제이기 때문에 플로이드 와샬 알고리즘을 적용해야 한다.
플로이드 와샬은 거쳐가는 정점을 기준으로 최단 거리를 구하는 알고리즘이다. 시간복잡도는 N^3으로 다익스트라 알고리즘보다는 오래 걸리지만, 음의 가중치가 있을 때나 간선의 수가 많을 때 사용하기 적절하다.
플로이드 와샬 알고리즘 설명) https://blog.naver.com/ndb796/221234427842
<문제 풀이 방법>
1) 자기자신으로 가는 비용을 제외한 나머지 비용을 INF로 초기화
2) fares 배열을 통해 연결되어 있는 정점 간 비용을 갱신
3) floyd warshall 알고리즘을 통해 정점 간 최소 비용을 갱신
4) (S ➡ (어느 정점) ➡ A) + (S ➡ (어느 정점) ➡ B)의 최소 비용 찾기
INF = 100000*200*200
def graphInit(n):
global graph
graph = [[INF for _ in range(n + 1)] for _ in range(n + 1)]
for i in range(n + 1):
for j in range(n + 1):
if i == j:
graph[i][j] = 0
def floyd(n):
global graph
for k in range(1, n + 1):
for i in range(1, n + 1):
for j in range(1, n + 1):
if graph[i][j] > graph[i][k] + graph[k][j]:
graph[i][j] = graph[i][k] + graph[k][j]
def solution(n, s, a, b, fares):
answer = INF
global graph
graphInit(n)
for fare in fares:
graph[fare[0]][fare[1]] = fare[2]
graph[fare[1]][fare[0]] = fare[2]
floyd(n)
for i in range(1, n + 1):
if answer > graph[s][i] + graph[i][a] + graph[i][b]:
answer = graph[s][i] + graph[i][a] + graph[i][b]
return answer
