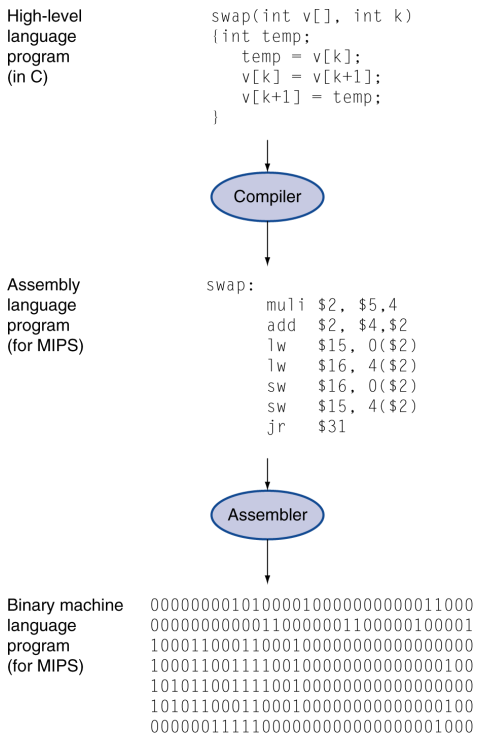
MIPS Instructions

---

0x01. High→Low 변환과정 예시

0x02. 소개

2.1 Definition

• Instructions(명령어)
  • instructions set 구조에 의해 정의되는 프로세서의 단일 연산
  • Opcode + Operand 지시자로 이루어짐
• Instruction set
  • 컴퓨터가 이해하는 모든 instruction(명령어)의 집합
  • 하드웨어 언어를 이해하는 것이 하드웨어/소프트웨어 인터페이스를 이해하는 핵심이다.
• RISC vs CISC
  • RISC : Reduced Instruction Set Computer
  • CISC : Complex Instruction Set Computer

2.2 컴퓨터 설계자의 목표

• 하드웨어나 컴파일러가 효율적으로 빌드할 수 있는 언어를 찾는 것.

  • performance를 극대화하고 cost와 energy를 최소화하는 것

• 장치의 단순성

  • KISS (Keep it short and simple or Keep it simple, stupid)의 원리

• MIPS (Microprocessor without Interlocked Pipeline Stages)

0x03. 컴퓨터 하드웨어의 연산(Operations)

• MIPS 산술 연산

add a, b, c # a = b + c
sub a, b, c # a = b - c

• e.g. f = (g+h) - (i+j) ;

add t0, g, h # t0 = g + h
add t1, i, j # t1 = i + j
sub f, t0, t1 # f = t0 - t1 = (g+h) - (i+j)

설계 원칙 1 : 단순함은 규칙성을 좋아한다..!

(1) 모든 산술 연산은 3개의 operands를 가진다.

(2) 규칙성은 implementation을 단순하게 만든다.

(3) 단순함은 저비용으로 더 높은 성능을 가능케 한다.

0x04. 컴퓨터 하드웨어의 피연산자(Operands)

• 명령어들(instructions)을 단순화하기 위해서는 산술 명령어(arithmetic instruction)의 피연산자들은 레지스터로 이루어져야한다.
  • RISC의 일반적 특징 중 하나
  • 컴파일러는 변수(variable)와 레지스터(register)를 연계시킨다.
  • 단순함은 규칙성을 좋아한다!

4.1 레지스터(Registers)

• 
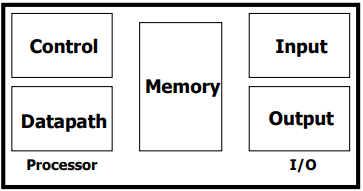
• On-chip scratchpad
• Datapath의 일부
• 자주 접근되는 데이터를 위해 사용
• MIPS는 32-bit 레지스터를 32개 가지고있다. (32*32)
• 레지스터는 $0 ~ $31로 표현한다.
• 32-bit 데이터는 워드(word)라고 불린다.

4.2 MIPS 레지스터

• 레지스터 32개
• 변수(Variables)를 위한 register ( 8개 )
  • $s0, $s1, $s2, ⋯ ,$s7
• 임시 레지스터(Temporary registers) ( 10개 )
  • $t0, $t1, $t2, ⋯ ,$t9

설계 원칙 2 : 작은 것이 더 빠르다.

레지스터 32개가 아니라 무지하게 많은 registers가 있으면?

(1) 프로그래머에게 편리함

(2) 그러나, 전기신호가 멀리까지 전달되어야 함

(3) 결국 clock cycle time이 증가하여 성능이 떨어짐

• e.g. f = (g+h) - (i-j) ;

/* int f, g, h, i, j; # 고급언어에서 이렇게 선언되었다고 가정
f, g, h, i, j         # 이 변수들은 각각 $s0, $s1, $s2, $s3, $s4와 대응 
*/
[Answer]
add $t0, $s1, $s2
add $t1, $s3, $s4
sub $s0, $t0, $t1

4.3 메모리 피연산자 (Memory Operands)

• 배열과 구조체

  • 데이터 요소들이 넘 많음..
  • 따라서, 레지스터가 아닌 메모리에 저장함.

• 메모리(Memory)

  • 주소(Address)와 데이터(Data)로 구성

• 데이터 이전 명령어(Data transfer instructions)

  • base address로 부터의 거리는 바이트단위로 적어주어야 한다.
  • load : lw (load word) 즉, 레지스터 ← 메모리 값
    • ex) lw reg memory      # reg ← memory
  • store: sw (store word) 즉, 레지스터 값→ 메모리
    • ex) sw reg memory      # reg → memory

참고 : lw는 load word, lh는 load half word, lb는 load byte이고,
sw는 store word, sh는 store half word, sb는 store byte이다.

• C언어에서 배열 접근 방식 (2개) :

  (1) direct addressing

       	char B[100], x, *p  B;
        p += 3; x =* p;

            (2) base addressing

       char B[100], x;
         x = B[3];

• e.g. g = h + A[8];

  • g = h + A[8];

      /* A의 base Address는 레지스터 $s3에 저장되었다고 가정
      고급언어에서 int g, h, A[100]; 라고 선언되었다고 가정
      */
      [Answer]
      lw $t0, 8($s3) # Wrong Answer
      	// $t0는 A[8]을 얻을까? ⋯ (X)
        # byte 단위로 32를 적어주어야 함!!
      	// 왜냐하면 int는 한 index당 4byte이기 때문!! (4byte*8=32)
      add $s1, $s2, $t0
      	# g = h + A[8]

4.4 메모리와 프로세스 하위시스템 (Memory and Processing Subsystems)

• 

4.5 하드웨어/소프트웨어 인터페이스

• Byte addressing

  • 하드웨어 구조는 하나의 word (4byte)에 접근하는 것이 아니라 1byte 데이터 접근을 지원한다. ↔ Word addressing

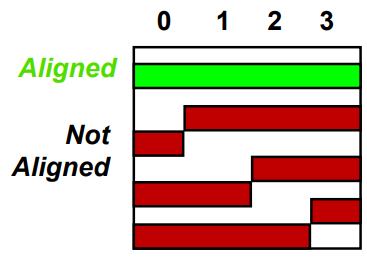
• 할당 제한(a.k.a memory alignment restriction)

  • 반드시 data 크기의 배수에 해당하는 메모리주소에 데이터를 넣는것
  • 예를 들어 워드는 반드시 4의 배수에 해당하는 주소에 할당되어야 한다.
  • Why? 이것이 CPU가 Memory를 다루는 방식이기 때문에 위처럼 할당할 경우 그렇지 않은 경우보다 속도측면에서 우월하기 때문
  • 

• 엔디안(Endianness)

  • Jonathan Swift의 소설 '걸리버 여행기' 로부터 유래
  • 리틀 엔디안(Little endian)
    • 낮은 주소에 데이터의 가장 낮은 바이트(LSB,Least Significant Bit)부터 저장
    • Intel IA-32, DEC PDP 11, VAX-11, Alpha, Atmel AVR
  • 빅 엔디안(Big endian)
    • 낮은 주소에 가장 높은 바이트(MSB, Most Significant Bit)부터 저장
    • MIPS, IBM S/360 and S/370, Motorola 680x0, SPARC, PA-RISC
  • 바이 엔디안(Bi-endian)
    • ARM, IA-64, PowerPC, Alpha, SPARC V9, MIPS, PA-RISC
  • ex1) 메모리 M[200]로 부터 → 레지스터 $s1으로 Load
    • lw $s1, 200($zero)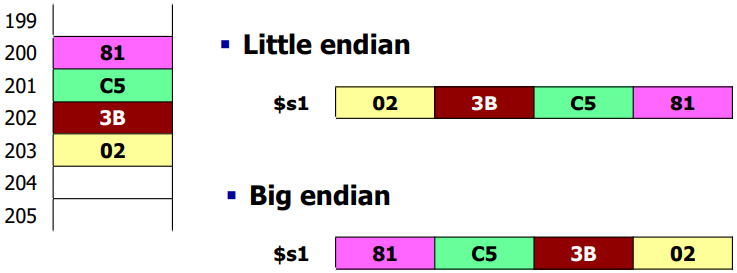
    • 
  • ex1) ex2) 레지스터 $s2를 → 메모리 M[100]에 Store
    • sw $s2, 100($zero)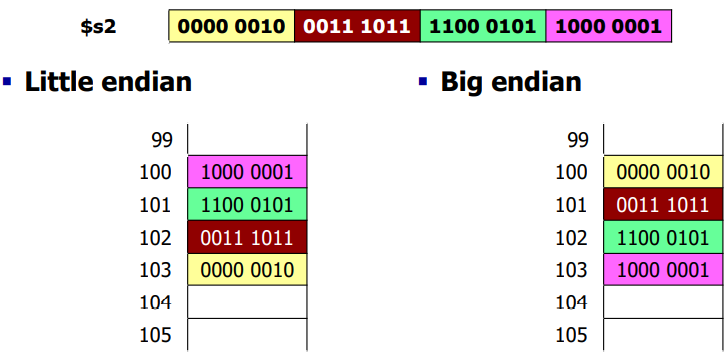
    • 

• Example: A[12] = h + A[8] ;

      /* A의 base address를 레지스터 $s3에 저장한다고 가정
      h가 $s2에 저장된다고 가정
      */
      [Answer]
      lw $t0,32($s3)   # 임시 레지스터. 메모리 A[8]을 레지스터 $t0에 load
      add $t0,$s2,$t0  # 임시 레지스터. 결과인 h+A[8]을 $t0에 저장 
      sw $t0,48($s3)   # 다시 레지스터 $t0(결과값)을 메모리 A[12]에 store

4.6 상수 피연산자(= Constant Operands, Immediate Operands)

• 상수 피연산자

  • x = x + 7 ;

• If, 상수 피연산자없이 $s3와 4를 더한다면??

      lw $t0, AddrOfConstant4 ($zero) //  $t0 = constant 4
      add $s3, $s3, $t0	         //$s3 = $s3 + $t0 (지금 $t0는 4가 들어있음)

위 방법은 비효율적!!!

• 해결책 : addi(add immediate) 명령어

  • addi $s3, $s3, 4       //  $s3 = $s3 + 4

• 흔하게 사용되는 것을 빠르게 만들자 !!!!

  • 상수 피연산자는 흔하게 사용된다.
  • 특히 상수 피연산자로 산술 연산 하는 경우가 많다.
  • 이걸 만들자 !! (addi, subi)