앞부분까지는 C언어로 코딩을 했을 때 어떻게 컴퓨터가 이해할 수 있는 언어로 변환되는가에 대해서 공부했다. 예를 들어 a=b+c; 를 할 때, add a, b, c가 되고 op,rs,rt,rd,shamt,funct의 비트를 알았지만, 여기서 rt와 rd가 더해지는 과정 즉, ALU의 연산과정을 빼먹었었다. 이제부터는 CPU자체의 연산에 대해 알아보자.
0x01. 컴퓨터에서 숫자의 표현
1.1 개요
(1) 정수(Integers)
- 정수의 표현
- Unsigned integers
- Signed integers
- 정수의 연산
- 덧셈, 뺄셈
- 곱셈, 나눗셈
- 표현할 수 있는 수를 넘어선 overflow가 나타날 경우 어떻게 해야하나?
(2) 실수(Real numbers)
- 소숫점의 표현(Floating-point)
- IEEE 754 표준에서 만듬
- 실수의 연산
- 덧셈, 뺄셈
- 곱셈, 나눗셈
1.2 Signed와 Unsigned 라는 숫자


1.3 음수의 표현 방법
- 총 3가지가 있다.
- Signed magnitude
- 1의 보수
- 2의 보수
(1) Signed Magnitude
📝 MSB가 1이면 음수, 0이면 양수로서 부호로 사용하고, 나머지를 진짜 숫자로 사용.
-
최대값
-
최솟값
-
이렇게 표현할 때 문제가 있다. 2진수의 계산이 힘들어 진다는 것이다.
-
예를 들어 0001은 1, 1001은 -1 을 더해보면
1001 + 0001 = 1010
(-1) (1) (0 이어야 함) 의미상으로 는 0000이 나와야 하나 실제는 다르게 나온다.
-
이것을 해결하기 위해 나온 것이 1의 보수이다.
(2) 1의 보수(1's complement)
📝 음수를 표현할 때 2진수 0을 1로, 1을 0으로 바꾼다. 즉 뒤집는다.
-
양수는 (1)의 방식과 똑같다.
-
그러나 음수의 표현이 다르다.
-
표현범위 :
-
요거는 그나마 괜찮은데 +0, -0이 나와서 쫌 그렇다. 이걸 개선한게 2의 보수이다.
(3) 2의 보수(2's complement)
📝 (1의 보수) + 1 이 2의 보수 표현이다.
-
역시 양수의 표현은 위 (1),(2)의 방식과 같다.
-
그러나, 또 음수의 표현이 다르다.
-
표현범위 : ,
-
덧셈기호만으로 뺄셈을 할 수가 있으므로 효율성이 높다.
- ex) a-b = a+(-b)
쉽게 2의 보수를 구하는 방법: 처음나오는 나오는 1을 놔두고 왼쪽부분을 다 뒤집는다.
ex) (10진법으로 6)에서 처음나오는 1을 놔두고 좌측 010을 101로 뒤집는다. 그럼 1011이 -6이된다.
1.4 signed, unsigned일 때 MIPS 산술 명령어
- $t1이 32-bit binary 1111 0101 ⋯ 0101을 포함하고 있다면
slt $t0, $t1, $zero$t0에는 무엇이 저장될까? - 그 결과는 $t1이 signed냐 unsigned냐에 따라 달라진다.
- 따라서, 컴파일러나 프로그래머는 slt를 사용할지 sltu를 사용할지를 꼭 고려해야한다.
- [The answer]
slt $t0, $t1, $zero: $t0에 1 저장sltu $t0, $t1, $zero: $t0에 0 저장
0x02. 컴퓨터의 2진수 덧셈과 뺄셈
2.1 덧셈 뺄셈
- 컴퓨터에서 2진수의 덧셈은 10진수의 덧셈과 동일하다.
- 하지만, 뺄셈은 다르다.
- 예를들어 A-B를 할 때 A+(-B)로 바꾼다.
- -B는 B의 1의보수(B') + 1 이다.
- 따라서, A-B = A+B'+1
- 예시) 7+6을 이진법으로 더하고 빼시오.
- [덧셈]
- 0000 0000 0000 0000 0000 0000 0000 0111 = 7
- 0000 0000 0000 0000 0000 0000 0000 0110 = 6
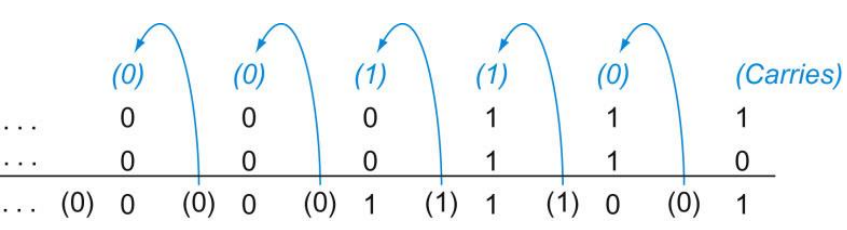
- 가장 오른쪽 비트 연산은 1+0이다. 합은 1이고 올림수(carries)는 0이다.
- 두 번째 자리 덧셈은 0+1+1이다. 합은 0이고 올림수(carries)는 1이다.
- 세 번째 자리 덧셈은 1+1+1이다. 합은 1이고 올림수(carries)도 1이다.
- 네 번째 자리 덧셈은 1+0+0이다. 합은 1이고 올림수(carries)는 없다.
- [뺄셈]
- <1. 그냥 빼기>
- 0000 0000 0000 0000 0000 0000 0000 0111 = 7
- 0000 0000 0000 0000 0000 0000 0000 0110 = 6
- 그냥 바로 뺄셈을 하여 0000 0000 0000 0000 0000 0000 0000 0001 = 1이 나올 수도 있다.
- <2. 보수 이용하기> : 7+(-6) = 7 + (6'+1)
- 0000 0000 0000 0000 0000 0000 0000 0111 = 7
- 1111 1111 1111 1111 1111 1111 1111 1010 = -6
- 이제 두 바이너리를 더하면 0000 0000 0000 0000 0000 0000 0000 0001 = 1이 나온다.
2.2 오버플로우
(1) 오버플로우란?
- 컴퓨터가 표현가능한 수는 한계가 있다.
- 32bit 레지스터를 사용하는 컴퓨터는 이다.
그런데 한계의 범위를 벗어나면 ❓❓❓
-
그것이 오버플로우다.
-
예를 들어 4-bit짜리가 있다. 그럼 표현가능한 수는 즉 -8 ~ 7 이다. 이제 5+4를 해보자. 인간이 봤을 때 0101 + 0100 = 1001이므로 9이다. 컴퓨터에서도 과연 그럴까?
- 컴퓨터는 반드시 MSB를 신경써야 한다. 1001의 MSB가 1이므로 음수이다. 이 수에다 2의 보수를 취해보면 7이므로 2진수 1001은 -7이다.
- 그러나, 사실 9가 나와야하는데 컴퓨터 저장 용량의 한계로 인해 9가 아니라 -7이라는 숫자가 나와버렸다. 즉 오버플로우 되어버렸다.
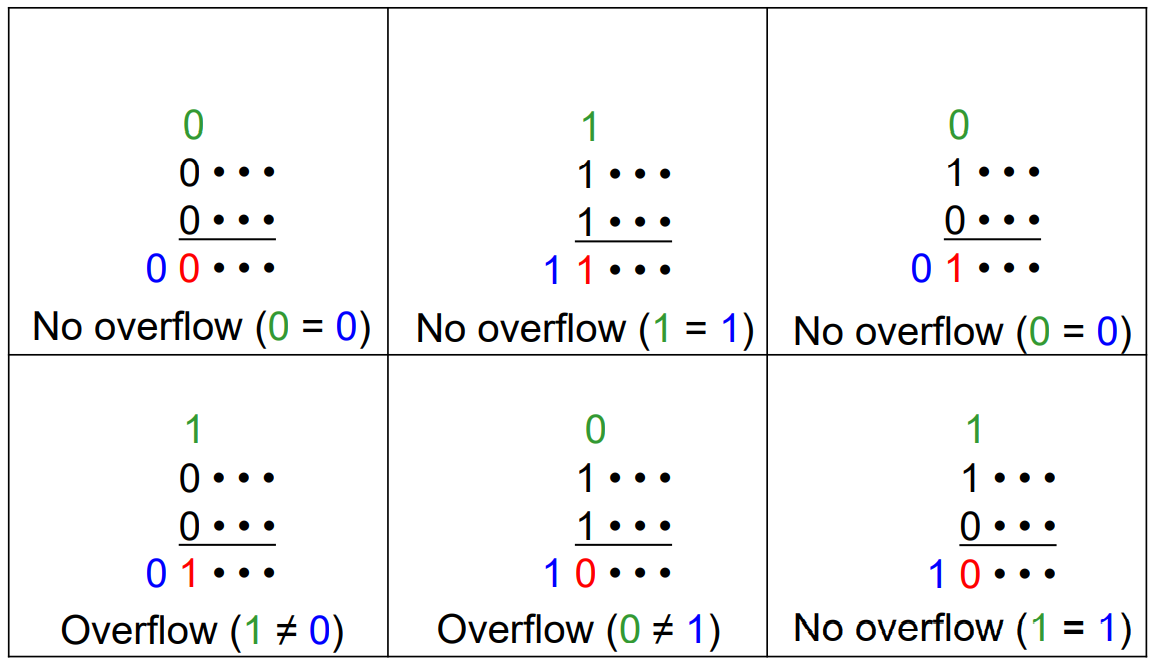
(2) 오버플로우 특징
- 음수와 양수를 더할 때는 오버플로우가 나지 않는다.
- 두 양수를 더했을 때 MSB가 1이라면 오버플로우가 난다.(양수+양수=음수가 되었으므로)
- 두 음수를 더했을 때 MSB가 0이라면 오버플로우가 난다.(음수+음수=양수가 되었으므로)
- 즉, MSB의 CarryIn 과 MSB의 CarryOut이 같지 않을 때 발생한다.
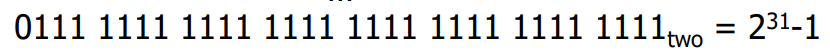
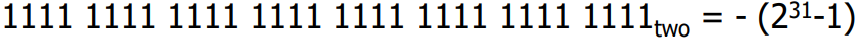





지나가던 사람입니다. 오버플로우된 숫자의 처리방식에 대해서 궁금했는데 잘 보고 갑니다.