Chapter 2: Intro to Relational Model

서강대학교 - 정성원 교수님의 강의 및 강의자료를 바탕으로 정리하였습니다.

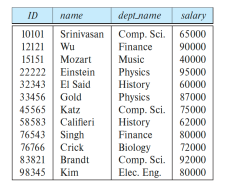
Instructor의 관계를 나타낸 예 (Table)

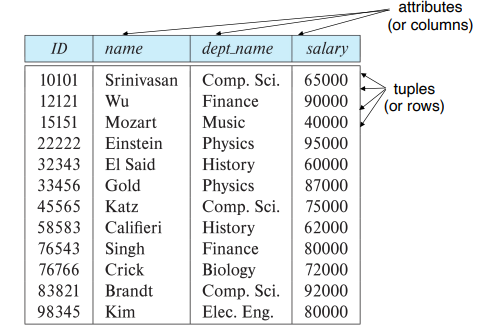
Relation Schema and Instance

• Attributes (속성) : 위 테이블의 열을 의미하며 테이블이 가지는 특성을 나타낸다.
• Relation Schema, R : 테이블의 구조를 정의한 것으로, 속성들의 집합이다. 위의 테이블에서의 relation schema는 Instructor = (ID, name, dept_name, salary)가 된다.
• Relation Instance, r(R) : 관계 스키마에 대한 실제 데이터의 집합이다. 테이블의 현재 값으로 표현되며, 테이블의 각 행은 튜플로 구성된다.

Attributes

Domain : 속성이 가질 수 있는 값들의 집합을 도메인이라고 한다. 속성 값은 일반적으로 원자적(atomic)이어야 하며, 즉, 더 이상 나눌 수 없는 값이어야 한다. null 값은 모든 도메인에 속해 있으며, 이는 해당 값이 "알 수 없음"을 의미한다. null 값은 많은 연산의 정의를 복잡하게 만든다.

Atomic
예를 들어, 02-xxx와 같은 전화번호에서 서울이라는 정보를 얻을 수 없어야한다.

튜플의 순서는 관계형 데이터베이스에서 중요하지 않다. 튜플은 임의의 순서로 저장될 수 있다. 예를 들어, 다음과 같은 'Instructor' 관계에서 튜플의 순서는 무관하다.

Database Schema

Database Schema: 데이터베이스의 논리적 구조
Database instance: 특정 시점에서의 데이터베이스 내 데이터의 스냅샷

Schema:'Instructor' (ID, 이름, 학과명, 급여)로 구성
Instance: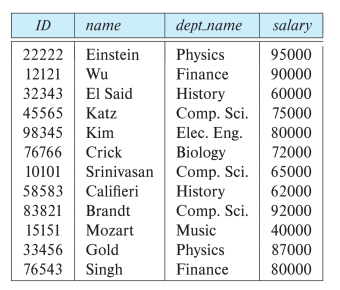

Keys

Key는 굉장히 중요한 개념이다. 완벽하게 이해할 수 있어야한다.

• SuperKey (슈퍼키) : 속성 집합 K가 관계 R의 모든 튜플을 고유하게 식별할 수 있으면 K는 R의 슈퍼키이다. 예를 들어, {ID}와 {ID, name}은 둘 다 'Instructor'의 슈퍼키이다. 따라서, 테이블 마다 가능한 키가 달라진다.
• 후보키(Candidate Key): 슈퍼키 K가 최소한의 속성 집합이면 후보키이다. 예를 들어 {ID}는 'Instructor'의 후보키이다. 그러나, {ID, name}은 최소집합이 아니기 때문에 아니다.
• 기본키(Primary Key): 후보키 중 하나를 기본키로 선택한다.
• 외래키(Foreign Key) 제약: 한 관계에서의 값이 다른 관계에서도 나타나야 한다. 참조하는 관계, 참조된 관계 등이 포함됩니다. 예를들어, 'Instructor'에서 'dept_name'은 'department' 테이블을 참조하는 외래 키이다. 이때, 'Instructor' 테이블의 어떤 튜플의 'dept_name' 열에 나타나는 값은 반드시 'department' 테이블의 'dept_name' 열의 적어도 하나의 튜플에도 나타나야 한다는 것을 의미한다. 이를 Referential integrity constraint라 한다. 'dept_name'은 'department' 테이블에서 primary key이다.

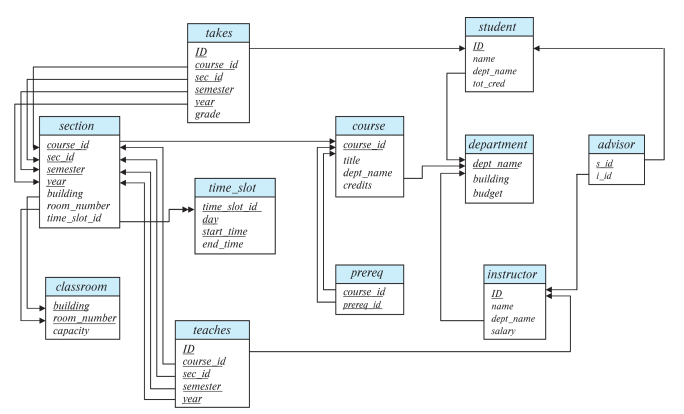
마찬가지로 'section' 테이블의 'time_slot_id' 열에서 'time_slot' 테이블의 'time_slot_id' 열을 참조하는 것도 참조 무결성 제약 조건을 나타낸다.

Relational Query Languages

검색용이다. 절차적(Procedural)과 비절차적(Non-procedural) 또는 선언적(Declarative) 언어로 구분된다. "Pure" query 언어는 관계 대수, 튜플 관계식 계산, 도메인 관계식 계산 등이 있지만, 관계 대수에 대해서만 다룬다! (SQL언어의 이론적 기반이다.)

그러나 이런 RQL은 모든 문제를 해결할 수 없다. 이는 RQL이 SQL과 같은 관계형 데이터베이스 언어들이 갖는 공통한 한계이다.

Relational Algebra

관계형 대수는 하나 또는 두 개의 관계를 입력으로 받아 새로운 관계를 결과로 반환하는 연산들의 집합으로 이루어진 절차적 언어(procedural language)이다.

• select: s
• project: π
• union: È
• set difference: –
• Cartesian product: x
• rename: r

Select

주어진 조건(예측)을 만족하는 튜플을 선택한다.
Notation: σ_p(r), 여기서 p는 selection predicate라 부른다.

예: 'Instructor'에서 'Physics' 학과를 선택
쿼리: σ_dept_name="Physics"(instructor)

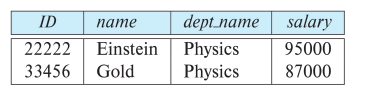
선택 조건에서는 =, ≠, >, ≥, <, ≤와 같은 비교 연산자를 사용할 수 있다. 또한, ∧ (and), ∨ (or), ¬ (not)을 이용해 predicates를 조합해서 더 큰 predicate를 만들어 사용가능하다.

예: 'Physics' 학과에서 연봉이 90,000달러 초과
σ_dept_name="Physics"∧salary>90,000(instructor)

선택 조건에는 두 속성 간의 비교를 포함할 수 있다.

예: 학과 이름이 건물 이름과 같은 모든 학과
σ_dept_name=building(department)

Project

일부 속성이 제외된 상태를 반환환다. 다르게 말해서, 선택된 속성으로 이루어진 테이블을 반환한다.
Notation: π_A1,A2,A3...Ak(r), 여기서 A1, A2, ..., Ak는 속성 이름이고 r은 관계 이름이다.
관계는 집합이기 때문에 중복행은 제거 된다.

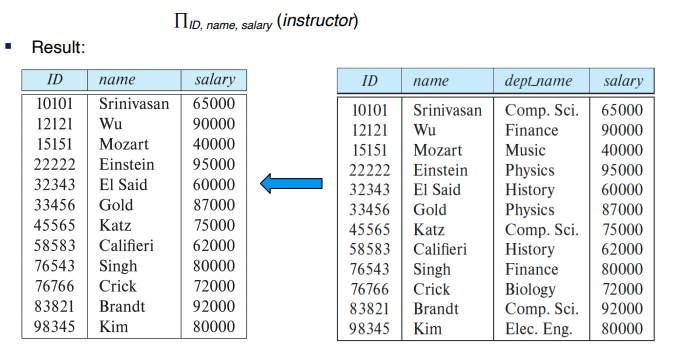
관계형 대수 연산의 결과는 관계이므로, 관계형 대수 표현식으로 관계형 대수 연산을 함께 구성할 수 있다. 위에서 배운 select와 project를 함께 서서 다음과 같이 나타낼 수 있다.
π_name(σ_dept_name =“Physics” (instructor))

Cartesian-Product

최적화의 핵심이 되는 연산이다. Cartesian-Product은 두 관계의 정보를 결합할 수 있게 해준다. 예를 들어, Instructor X Teaches 처럼 사용할 수 있다.
이때, 각각의 가능한 튜플 쌍(하나는 강사 관계, 다른 하나는 강의 관계에서)을 사용하여 결과의 튜플을 구성한다. 또한, ID 속성이 두 관계에 모두 존재하므로 원래 관계에서 해당 속성이 어디에서 왔는지 구별하기 위해 속성 앞에 관계 이름을 붙인다.

• instructor.ID
• teaches.ID
  
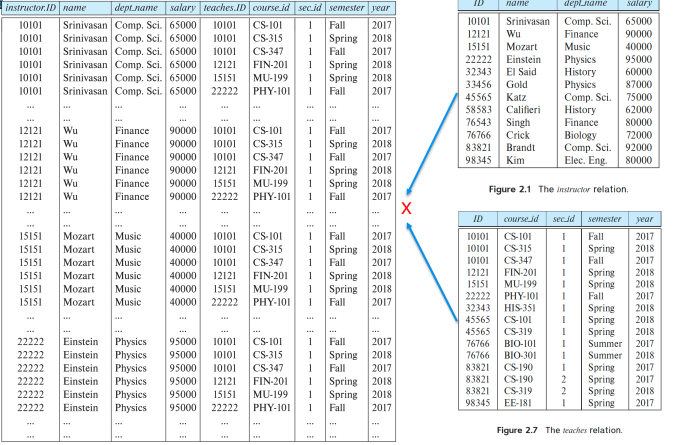
  하지만, 시간이 많이걸린다.

Join

Cartesian-Product의 경우 모든 튜플을 결합한다. 따라서, 대부분의 결과 행은 특정 과정을 가르치지 않은 instructor에 대한 정보를 포함하게 된다.

instructor와 그들이 가르친 과정에 관한 튜플만 얻기 위해 다음과 같이 작성한다.
σ_instructor.id = teaches.id (instructor x teaches ))

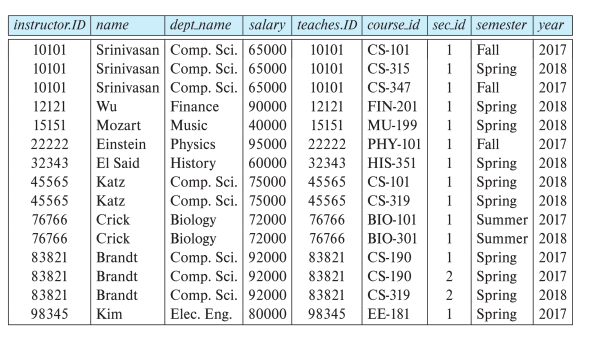
즉, Join연산은 select 연산과 Cartesian-Product연산을 결합한 연산이다.
2개의 관계 r(R)과 s(S)가 있을 때, 어떤 predicate 'theta'에 대해 다음과 같이 정의된다.

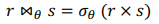
Union

두 관계를 결합하는 연산이다.
Notation: r U s
이때, r U s가 유효하려면 다음과 같은 조건이 필요하다.

• r과 s는 같은 arity(속성의 동일한 개수)를 가져야 한다.
• 속성 도메인이 호환되어야 한다(예: r의 두 번째 열이 s의 두 번째 열과 같은 유형의 값을 처리).
  만약, 2017년 가을 학기에 가르친 모든 과목, 또는 2018년 봄 학기에 가르친 모든 과목, 또는 둘 다 찾으려면 다음과 같이 작성한다.
  

Set-Intersection

두 관계에 모두 존재하는 튜플들을 찾을 수 있다.
Notation: r ∩ s
Union과 마찬가지로 다음 가정이 필요하다.

• r과 s는 같은 arity(속성의 동일한 개수)를 가져야 한다.
• 속성 도메인이 호환되어야 한다. (compatible)

만약, 2017년 가을 학기와 2018년 봄 학기에 모두 가르친 과목 집합을 찾으려면 다음과 같이 작성한다.

Set Difference

집합에서 배우는 차집합과 비슷한 처리를 한다. 두 관계에서 한쪽 관계에만 존재하는 튜플을 찾을 수 있다.
Notation: r - s
마찬가지로 다음 조건을 만족해야한다.

• r과 s는 같은 arity(속성의 동일한 개수)를 가져야 한다.
• 속성 도메인이 호환되어야 한다. (compatible)

만약, 2017년 가을 학기에 가르친 모든 과목을 찾되, 2018년 봄 학기에는 가르치지 않은 과목을 찾으려면 다음과 같이 작성한다.

Assignment

관계형 대수 표현식을 작성할 때 일부를 임시 관계 변수에 할당하는 것이 편리할 때가 있다. 할당 연산은 <- 기호로 나타내며 프로그래밍 언어에서의 할당처럼 작동한다.

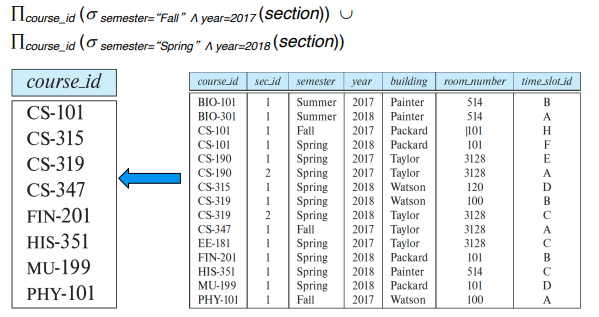
만약, "Physics" 학과와 Music 학과의 모든 강사를 찾으려면 다음과 같이 작성한다.

할당 연산을 사용하면 쿼리를 일련의 할당 후에 표현식이 있는 순차 프로그램으로 작성할 수 있으며, 해당 표현식의 값이 쿼리 결과로 표시된다. 따라서, 할당 연산을 사용하면 관계형 대수 쿼리를 효과적으로 표현할 수 있으며, 여러 단계로 분할하여 문제를 해결할 수 있다. 이는 프로그래밍에서 변수를 사용하여 복잡한 계산을 단계별로 나누는 것과 비슷하다. 이로 인해 쿼리의 가독성이 향상되고 오류를 줄일 수 있다.

Rename

관계형 대수 표현식의 결과는 참조할 수 있는 이름이 없다. 이러한 목적을 위해 이름 바꾸기 연산자 $\rho$ 를 사용한다.
Expression: $\rho_{x}(E)$, 이름 x로 표현식 E의 결과를 반환한다. $\rho_{x(A1,A2,...An)}(E)$ 로도 쓸 수 있다.

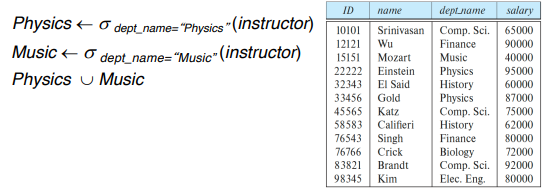
ID가 12121인 강사보다 더 많이 버는 강사의 ID와 이름

Equivalent Queries

관계형 대수에서 쿼리를 작성하는 방법은 여러 가지가 있다.
예로, Physics 학과에서 급여가 90,000보다 높은 강사가 가르치는 과목에 대한 정보를 찾으려면 다음 2가지 쿼리가 가능하다.

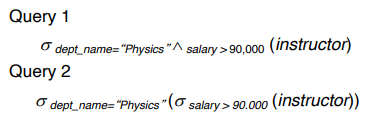
두 쿼리는 동일하지 않지만, 동등하다. 즉, 모든 데이터베이스에서 동일한 결과를 제공한다.

하지만, 동등한 쿼리라 할지라도 명확하게 더 나은 쿼리가 존재한다. 첫 번째 쿼리를 보면 두 테이블을 먼저 join한다. 이후, physics 학과를 찾는다. 반면, 두 번째 쿼리의 경우 우선적으로 dept_name이 physics을 찾은 후, join한다. 각 쿼리의 시간을 살펴보면 첫 번째의 경우 12 * 15의 튜플을 생성하고 찾으므로 180만큼 걸리지만, 두 번째의 경우 12개에서 2개를 먼저 찾은 후, 테이블과 join을 하기 때문에 훨씬 더 적은 시간이 걸린다.

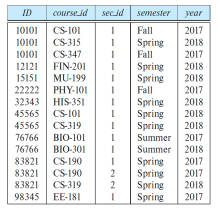
여기까지가 chap2의 내용이다.