1. Softmax Regression

@Tommy Kim

regression 문제는 하나의 label에 대해 얼마나 많은가?와 같은 연속적인 값을 예측하는 문제이다. 하지만, 현실 세계의 supervised learning 문제는 회귀 문제 말고도 ‘분류’ 문제도 존재한다. 분류 문제는 얼마나 많은가?가 아닌 어떤 카테고리에 속하는가?에 대한 질문을 대답하는 문제이다.

• 메일이 스팸인지 아닌지
• 고객이 구독 서비스에 가입할지 아닐지
• 이미지에 있는 객체가 무엇인지 (원숭이, 강아지, 고양이, 닭 등)
• 고객이 어떤 물건을 구매할 것인지

분류 문제는 크게 두 가지 task로 나뉘게 된다.

• hard assignments : 단순히 데이터가 어느 label에 속하는 지에만 관심이 있다.
• soft assignments : 각각의 카테고리의 확률들을 평가한다.

분류 문제는 두 개의 label이 동시에 true인 경우도 존재한다. 가령, 뉴스 기사의 경우에도 경제, 항공 우주, 예능을 동시에 다루는 기사이면, 뉴스 기사의 주제는 두 가지 이상이 된다.

1) Classification

분류 문제를 이해하기 위해, 먼저 2 X 2 크기의 grayscale(흑백) 이미지가 있다고 가정하자. 우리는 각각의 픽셀을 스칼라들로 표현할 수 있다 : $x_1, x_2, x_3, x_4$. 그리고 각각의 이미지는 고양이, 닭, 개 중에 하나라고 가정하자.

우리는 label의 값으로 {고양이, 닭, 개}를 단순한 숫자로 표현할 수 있다 : $y \in \{ 1,2,3\}$. 이 방법은 간단하지만, 각 동물들을 숫자 값이 커짐에 따라 분류하는 방법은 타당하지 않다. 나이에 따라 사람을 부르는 명칭(어린이, 청소년, 어른, 중년, 노인)은 위의 방법에 잘 맞을 수 있으나, 동물 분류 문제에서는 적합하지 않은 것이다. 이러한 문제를 해결하기 위해 통계 학자들은 one-hot encoding 방법을 개발하였다. 이 방법은 각 카테고리에 해당하는 요소만 1의 값을 할당하고, 그 외에는 0을 할당하는 방법이다. 원핫 인코딩으로 우리는 label을 재정의할 수 있다.

$y \in \{ (1,0,0),(0,1,0),(0,0,1)\}$

one-hot encoding vs label encoding

• 원핫 인코딩은 다양한 분류 상황에서 적용이 가능함(수치적 관계가 전무한 경우에도)
• 원핫 인코딩은 라벨 인코딩에 비해서 메모리의 문제가 발생할 수 있다 → computational 문제도 같이 발생
• test data에서 전혀 새로운 카테고리가 등장하면, 해당 카테고리를 추가하기가 어려움 → 입력 벡터들의 차원을 하나 더 추가해야 하므로, 추가 학습 작업도 필요하다

a. Linear Model

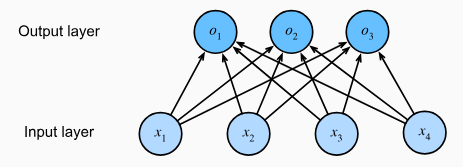
모든 카테고리와 관련된 조건부 확률을 추정하기 위해 여러 개의 출력을 가진 모델이 필요하다. 이를 선형 모델로 처리하기 위해 카테고리 수만큼의 affine function(원점을 지나지 않는 → 편향이 그 역할을 함)이 필요하다. 위의 경우에는 다음과 같은 수식으로 표현할 수 있다.

위의 네트워크를 그림으로 표현하면 다음과 같다. 이 그림에서 output은 fully connected layer라고 부른다.

우리는 위의 식을 벡터와 행렬을 이용해서 더 간단하게 표현할 수 있다.

여기서 가중치는 3 X 4크기의 행렬이고, 편향(bias)의 집합은 $\bf b \in \R^3$의 벡터이다.

b. The Softmax

학습을 위한 적절한 손실 함수로써 출력 값과 label사이의 차이를 최소화 하는 방법을 생각해볼 수 있는데, 이는 다음의 두 가지 이유 때문에 불가능하다.

• i번째 출력 $o_i$의 확률들의 합이 1이 된다는 보장이 없다.
• $o_i$의 확률들이 각각 음수가 아니라는 보장이 없다.

위의 두 가지 측면의 예시로, 누군가 집을 살 때 침실의 개수와 집을 살 확률이 선형 의존성을 보인다고 하자. 이때, 선형 조합의 계산 결과로 집을 살 확률이 1을 넘을 수 있기 때문에, 이러한 결과 값을 조정하는 방법이 필요하다.

위의 문제들을 해결하기 위해 output $\bf o$에 정규 분포를 따르는 노이즈 $\epsilon$을 추가하는 방법이 소개되었으나, 잘 작동이 되지는 않았다. 그 다음으로 소개된 방법은, 출력의 확률들에 지수를 씌우는 방법이 소개되었다. 이 방법은 음수로 계산된 확률도 양수로 만들어주는 장점이 있었다. 또한, 각 확률의 값이 양수임이 보장되었으므로, 각각의 확률을 $o_i$의 합으로 나누어주는 ‘정규화’ 방법을 채택해서 각 확률들의 합이 1이 보장이 안되었던 문제도 해결하였다. 이 방법을 우리는 ‘softmax’라고 한다.

위 식에서 알 수 있듯이, softmax 함수를 적용해도, $o_j$에서 가장 높은 확률의 카테고리는 변하지 않기 때문에 $\hat y$에서 예측된 카테고리를 선택할 때 softmax함수를 적용하지 않아도 알 수 있다.

c. Vectorization

효율적인 계산을 위해 우리는 데이터의 미니 배치들을 벡터화해서 표현할 수 있다.

2) Loss Function

이제 features $\bf x$에서 확률 $\hat y$로의 매핑을 찾아내었기 때문에, 정확도를 최적화 하는 방법이 필요하다. 이를 위해서 최대우도법(maximum likelihood function)을 사용할 것이다.

a. Log-Likelihood

softmax함수는 각 카테고리의 조건부 확률을 나타내는 벡터를 반환한다. 예를 들어 고양이 카테고리의 경우엔 다음과 같은 조건부 확률로 계산된다 : $\hat y_1 = P(y = \mathrm {cat} | x)$. 우리는 또한 벡터 표현식을 통해 label $\bf Y$는 원핫 인코딩 된 벡터임을 알 수 있다. label 벡터의 각 카테고리의 조건부 확률은 서로 독립이기 때문에 입력 $\bf X$에 대한 카테고리 $\bf Y$의 전체 조건부 확률은 다음과 같이 정리할 수 있다.

확률의 곱을 최대화 하는 문제는 해결하기 어렵기 때문에 우리는 위의 식에 로그와 음수를 취한 후, 확률들의 합을 최소화하는 문제로 바꾸어서 해결할 것이다.

여기서의 손실 함수 $\mathcal l$은 다음과 같이 정의한다.

위의 손실 함수는 cross-entropy loss라고도 불린다. 이미 $\bf y$가 원핫 인코딩된 벡터이므로, j = 1부터 q까지 합을 구할 때 해당하는 클래스 외에는 모든 항목이 0이 되어 사라진다. 또한 어떠한 클래스의 확률도 1을 넘지 않기 때문에, 최종적으로 손실 함수의 값은 0보다 작아질 수 없다.

여기서 loss function을 다시 살펴보자. 위의 식의 $\hat y_j$는 output에 softmax를 거친 후에 반환된 값이다. softmax 식을 생각해보면, $\hat y_j$가 1이 되려면 $o_j$의 값이 무한대가 되어야 하기 때문에 $l$ 값은 0이 될 수 없다. 반대로, $\hat y_j$가 0이 되려면 $o_j$의 값이 음의 무한대가 되어야 하는데, 이 역시 불가능하다.

b. Softmax and Cross-Entropy Loss

위의 softmax의 정의대로 손실함수의 $\hat y$의 값을 output $o$에 대한 식으로 바꿔주면 다음과 같다.

손실 함수를 미분 해보면 다음과 같다.

도함수를 분석해보면 softmax에 의해 할당된 확률과 실제 label의 값의 차이임을 알 수 있다. 위의 식 우리가 regression 문제를 해결할 때 보았던 모양과 유사함도 확인할 수 있다. 이러한 cross-entropy에 대한 개념은 정보 이론을 통해 더 명쾌하게 이해할 수 있다.

3) Information Theory Basics

정보 이론은 데이터의 인코딩, 디코딩, 전송 및 활용 문제에 쓰이는 이론이다.

a. Entropy

엔트로피란 데이터가 가지고 있는 정보의 양이다. 분포 P가 있을 때, 엔트로피 $H[P]$는 다음과 같이 계산된다.

엔트로피는 ‘nats’라는 단위를 쓰는데, 1 nat은 1.44 bit이다.

b. Surprisal

정보 이론에서 소개되는 예측과 압축의 관계는 비례 관계와 비슷한 관계를 가진다. 데이터의 패턴이 일정해서 예측하기 쉬운 형태이면, 압축하기도 쉽고, 예측이 어렵다면, 그만큼 압축하기도 어려운 관계이다.

정보 이론에서 사건을 완벽하게 예측하지 못한다면 놀람(surprisal)이라고 표현한다. 어떤 사건에 할당된 확률 $p(y)$에 대해 놀란 정도를 $-\log p(y)$로 정의했다. 즉, 낮은 사건의 확률일 수록, 더 큰 ‘놀람’을 가져오는 것이다. 위에서 정의한 엔트로피의 식은 이러한 ‘놀람’들의 기대값으로 정의된 식이다. 이는 곧 데이터 생성 과정을 정확히 반영하는 확률에 기반하는 식이다.

c. Cross-Entropy Revisited

그렇다면 cross-entropy는 어떤 식인가? 이 식은 두 분포 P와 Q에 대한 식 $H(P,Q) = \sum_j -P(j) \log Q(j)$로 바꾸어서 생각할 수 있다. 이는 주관적 확률 $Q$를 가진 관찰자가 실제 확률 $P$에 따라 생성된 데이터를 관찰했을 때 기대되는 ‘놀람’이다. 위의 $H$는 두 분포 $P, Q$가 동일할 때 최솟값을 가진다.

이에 따라 우리는 cross-entropy 손실 함수는 두 가지 역할을 한다고 생각할 수 있다 : 관찰된 데이터의 가능도를 최대화 하는 것 / 우리의 ‘놀람’ 정도를 최소화 하는 것

Q&A

@w2y multi-classification에서 softmax 적용하는 방법?

2. The Image Classification Dataset

@w2y

• 대표 Classification Dataset

  • MNIST(Modified National Institute of Standards and Technology database)
    : 손으로 쓴 숫자 데이터셋
  • 28x28 픽셀 해상도의 60,000(train), 10,000(test) 데이터셋으로 구성된다.
  • Deep networks(e.i., LeNet-5), SVM, Tanget distace classifier 등의 모델은 1%미만의 error를 갖는 성능을 보이며, 간단한 모델이라도 분류 정확도가 95% 이상에 달한다.

    강력한 모델과 그렇지 못한 모델을 구별하는데 적합하지 않음

    
    
  • ImageNet
  • 1,281,167(train), 50,000(test), 1,000개의 카테고리로 구성된 데이터셋 ~매우 크다.
  • Fashion-MNIST
  • 28x28 픽셀 해상도의 10개 카테고리의 의류 이미지가 포함되어 있다.

1) Loading the Dataset

%matplotlib inline # 브라우저 내부(inline) 에 바로 그려지도록 해주는 코드
import time
import torch
import torchvision
from torchvision import transforms
from d2l import torch as d2l

d2l.use_svg_display()

class FashionMNIST(d2l.DataModule): 
    """The Fashion-MNIST dataset."""
    def __init__(self, batch_size=64, resize=(28, 28)):
        super().__init__()
        self.save_hyperparameters()
        trans = transforms.Compose([transforms.Resize(resize),
                                    transforms.ToTensor()])
				# 데이터셋 다운(불러오기)
        self.train = torchvision.datasets.FashionMNIST(
            root=self.root, train=True, transform=trans, download=True)
        self.val = torchvision.datasets.FashionMNIST(
            root=self.root, train=False, transform=trans, download=True)

data = FashionMNIST(resize=(32, 32)) # 32x32 픽셀로 업스케일
len(data.train), len(data.val)
# > **(60000, 10000)**

대부분 최신 이미지 데이터에는 3개의 채널(빨간색, 녹색, 파란색)이 있고 초분광 이미지(hyperspectral)에는 100개 이상의 채널이 있을 수 있다.

일반적으로, 이미지는 $c \times h \times w$ tensor로 저장한다. ($c$ : 색상 채널 수, $h$ : 높이, $w$ : 너비)

data.train[0][0].shape
**# > torch.Size([1, 32, 32])**

Fashion-MNIST 데이터는 이해하기 쉽도록 라벨링되었다.

@d2l.add_to_class(FashionMNIST)
def text_labels(self, indices):
    """Return text labels."""
    labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
              'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [labels[int(i)] for i in indices]

2) Reading a Minibatch

@d2l.add_to_class(FashionMNIST)
def get_dataloader(self, train):
    data = self.train if train else self.val
    return torch.utils.data.DataLoader(data, self.batch_size, shuffle=train,
                                       num_workers=self.num_workers)
# 내장된 data iterator(;DataLoader)를 사용하여 batsh_size(64)만큼의 미치 배치 데이터를 읽음
# train 데이터 로더의 경우, shuffle을 적용

X, y = next(iter(data.train_dataloader()))
print(X.shape, X.dtype, y.shape, y.dtype)
**# > torch.Size([64, 1, 32, 32]) torch.float32 torch.Size([64]) torch.int64
# torch.Size[이미지 개수, channel 수, hight, width]**

3) Visualization

훈련 중인 데이터를 시각화하고 검사하는 것은 매우 좋다. 시각화를 통해 실험 설계 시 생긴 실수와 오류를 발견할 수 있다.

# 이미지와 관련 라벨을 시각화
def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5): 
    """Plot a list of images."""
		# 구현 세부 사항 pass - d2l.show_images를 호출하여 사용하면 됨;)
    raise NotImplementedError

@d2l.add_to_class(FashionMNIST) 
def visualize(self, batch, nrows=1, ncols=8, labels=[]):
    X, y = batch
    if not labels:
        labels = self.text_labels(y)
    d2l.show_images(X.squeeze(1), nrows, ncols, titles=labels)
batch = next(iter(data.val_dataloader()))
data.visualize(batch)

Q&A

3. The Base Classification Model

@리치

앞선 회귀와 마찬가지로, 분류 역시 프레임워크를 통한 간결한 구현이 가능하다.

1) The Classifier Class

분류 모델의 기본 클래스가 될 Classifier을 정의한다. ’validation_step’ 함수에서는 검증 데이터 배치에 대한 손실 값과 분류 정확도를 기록한다. 마지막 배치에서 개수가 차이날 수 있어 평균 수치가 정확하지 않을 수 있지만, 코드를 간단하게 유지하기 위해서 이 차이는 무시한다.

import torch
from d2l import torch as d2l

class Classifier(d2l.Module):  #@save
    """The base class of classification models."""
    def validation_step(self, batch):
        Y_hat = self(*batch[:-1])
        self.plot('loss', self.loss(Y_hat, batch[-1]), train=False)
        self.plot('acc', self.accuracy(Y_hat, batch[-1]), train=False)

또한, 기본적으로 SGD Optimizer를 사용한다. (선형 회귀와 마찬가지로 미니배치에 작용)

@d2l.add_to_class(d2l.Module)  #@save
def configure_optimizers(self):
    return torch.optim.SGD(self.parameters(), lr=self.lr)

2) Accuracy

예측 확률 분포 y_hat이 주어지고 hard prediction을 해야할 때 예측 확률이 가장 높은 클래스를 선택한다. (hard prediction은 예측 확률 분포를 기반으로 특정 클래스를 최종적으로 선택하는 과정이다.) 예를 들어, Gmail에서 이메일을 “Primary”, “Social”, “Updates”, “Forums”, 또는 “Spam” 중 하나로 분류해야 할 때, 최종 결과는 이 중 하나를 선택해야 한다.

예측이 레이블 클래스 y와 동일할 때 정확히 예측했다고 간주한다. 따라서, 분류에서의 정확도는 모든 예측 중 정확한 예측의 비율로 정의된다. 정확도는 미분이 불가능하기 때문에 최적화 하는 것이 어렵지만, 중요한 성능 지표이다.

만약, y_hat이 행렬이라면 두 번째 차원에 각 클래스에 대한 예측 점수가 저장되어 있다고 가정한다. 이때 각 행에서 가장 높은 예측 점수를 가진 클래스를 찾기 위해 argmax를 사용한다. 그 다음, 이 예측된 클래스(preds)를 실제 레이블(Y)과 원소별로 비교한다. 이때, == 기호는 데이터 타입에 민감하므로 항상 데이터 타입을 일치시켜야한다.

@d2l.add_to_class(Classifier)  #@save
def accuracy(self, Y_hat, Y, averaged=True):
    """Compute the number of correct predictions."""
    Y_hat = Y_hat.reshape((-1, Y_hat.shape[-1]))
    preds = Y_hat.argmax(axis=1).type(Y.dtype)
    compare = (preds == Y.reshape(-1)).type(torch.float32)
    return compare.mean() if averaged else compare

4. Softmax Regression Implementation from Scratch

@Tommy Kim

1) Defining the model and loss function

#필요한 라이브러리 불러오기
import torch
from d2l import torch as d2l

#softmax함수 정의하기
def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp.sum(1, keepdims=True) #파라미터를 1로 해야 행을 기준으로 sum함
    return X_exp / partition  #broadcasting 연산이 진행됨

#모델 정의하기
class SoftmaxRegressionScratch(d2l.Classifier):
    def __init__(self, num_inputs, num_outputs, lr, sigma=0.01):
        super().__init__()
        self.save_hyperparameters()
        self.W = torch.normal(0, sigma, size=(num_inputs, num_outputs),
                              requires_grad=True)
        self.b = torch.zeros(num_outputs, requires_grad=True)

    def parameters(self):
        return [self.W, self.b]

@d2l.add_to_class(SoftmaxRegressionScratch) #forward 코드 class에 추가
def forward(self, X):
    X = X.reshape((-1, self.W.shape[0]))
    return softmax(torch.matmul(X, self.W) + self.b)

# 손실함수 cross-entropy 정의하기
def cross_entropy(y_hat, y):
    return -torch.log(y_hat[list(range(len(y_hat))), y]).mean()

# 정의한 손실함수 모델에 추가하기
@d2l.add_to_class(SoftmaxRegressionScratch)
def loss(self, y_hat, y):
    return cross_entropy(y_hat, y)

위의 모델을 바탕으로 fashion MNIST 데이터를 학습 해보면 다음과 같다.

data = d2l.FashionMNIST(batch_size=256) #배치 사이즈 256
# 28 X 28 픽셀의 이미지 데이터(1차원으로 표현하면 784개의 features)
# 구별해야할 카테고리 10개(output)
model = SoftmaxRegressionScratch(num_inputs=784, num_outputs=10, lr=0.1)
trainer = d2l.Trainer(max_epochs=10)
trainer.fit(model, data)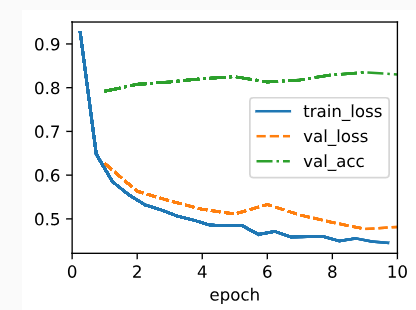

학습된 모델을 예측한 결과는 다음과 같다.

X, y = next(iter(data.val_dataloader()))
preds = model(X).argmax(axis=1)

wrong = preds.type(y.dtype) != y
X, y, preds = X[wrong], y[wrong], preds[wrong]
labels = [a+'\n'+b for a, b in zip(
    data.text_labels(y), data.text_labels(preds))]
data.visualize([X, y], labels=labels)

5. Concise Implementation of Softmax Regression

@w2y

1) Defining the Model

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

class SoftmaxRegression(d2l.Classifier):
    """The softmax regression model."""
    def __init__(self, num_outputs, lr):
        super().__init__()
        self.save_hyperparameters()
				# 내장 레이어를 사용하여 완전 연결 레이어를 구성
        self.net = nn.Sequential(nn.Flatten(),
                                 nn.LazyLinear(num_outputs))

    def forward(self, X):
        return self.net(X) # 4차 tensor - Flatten() -> 2차 tensor # 첫 번째 축(이미지 개수)의 차원

2) Softmax Revisited

모델의 출력을 계산하고 교차 엔트로피 손실을 적용하는 것이 맞지만, 지수의 계산은 underflow(연산의 결과가 취급할 수 있는 수의 범위 보다 작아지는 상태) 또는 overflow(허용된 가장 큰 값보다 더 커져서 실제로 저장되는 값은 아주 작은 수이거나 음수가 되는 상태) 위험이 있다.

Softmax 함수로 확률 $\hat{y}$를 구하는 것을 고려해봤을 때, output $o_{k}$가 큰 경우 $\exp(o_{k})$가 특정 데이터 유형에 대해 가질 수 있는 가장 큰 숫자보다 클 수 있다(=overflow). 또는 매우 큰 음수가 될 수 있다(=underflow).

이에 따라 $\bar{o} = \max_{k}o_{k}$를 빼 계산한다.

$o_{j} - \bar{o} ≤ 0$를 만족하므로, q개의 클래스 분류 문제의 경우 분모는 [1, $q$] 사이의 값을 가지고 분자는 1을 초과하지 않아 overflow를 방지할 수 있다.

이 때, $\exp (o_{k}-\bar{o})=0$인 경우 $\log \hat{y}_{j}=\log 0$이 되고 역전파 단계에서 NaN이 출력될 수 있다.

Softmax와 Cross-entropy를 결합하여 계산하면 문제를 해결할 수 있다(+overflow/underflow 방지).
Softmax 확률을 새 loss function에 전달하는 대신, ‘LogSumExp trick’ 방식으로 교차 엔트로피 손실 함수 내에서 로짓(logits)을 전달하고 소프트맥스와 해당 로그를 한 번에 계산한다.

• 모델에 의한 output 확률을 평가하기 위해 기존 소프트맥스 기능 유지

@d2l.add_to_class(d2l.Classifier) 
def loss(self, Y_hat, Y, averaged=True):
    Y_hat = Y_hat.reshape((-1, Y_hat.shape[-1]))
    Y = Y.reshape((-1,))
    return F.cross_entropy(
        Y_hat, Y, reduction='mean' if averaged else 'none')

3) Training

Flattened 된 784차원의 특성 벡터를 사용하여 모델을 학습한다.

data = d2l.FashionMNIST(batch_size=256)
model = SoftmaxRegression(num_outputs=10, lr=0.1) #카테고리 수: 10, learning rate=0.1
trainer = d2l.Trainer(max_epochs=10)
trainer.fit(model, data)

꽤 낮은 에러로 수렴한다.

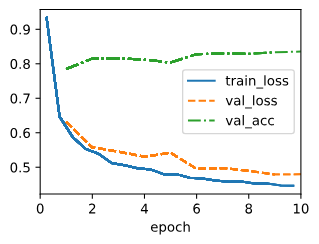
6. Generalization in Classification

@리치

항상 우리의 목표는 이전에 보지 못한 데이터(테스트 세트)에서 경험적으로 평가된 일반적인 패턴을 학습하는 것이다. 즉, 훈련 데이터 셋에 대해 정확도가 높다는 것은 의미가 없다. 이런 관점에서 아래와 같은 중요한 질문이 생긴다!

• 기본 모집단에 대한 분류기의 정확도를 제대로 추정하려면 얼마나 많은 테스트 예제가 필요한가?
• 동일한 테스트에서 모델을 계속 반복적으로 평가하면 어떤일이 일어나는가?
• 훈련 세트에 선형 모델을 적합시키는 것이 단순한 암기보다 왜 더 나을 것으로 기대하는가?

일반화를 사전에 보장할 수 있는 몇 가지 경우가 있다: 많은 모델들의 경우, 일반화 갭 $\epsilon$의 원하는 상한에 대해, 어떤 분포로부터 생성된 데이터라도 경험적 오차가(empirical error) 실제 오차의 $\epsilon$내에 위치하도록 샘플 수 n을 결정할 수 있다.

당연하게도 딥러닝 실무자들에게는 실용성이 크지않다. 따라서, 보통 이러한 보장을 포기하는 대신 과거유사한 문제에서 일반화가 잘 이루어졌던 방법을 사용하고 경험적 평가를 통해 사후에 일반화를 증명하는 경우가 많다.

1) The Test Set

일반화 오류를 평가하기 위한 표준 방법은 테스트 세트이다. 분류기 f가 있다고 가정하자. 또한, f에 훈련시키지 않은 새로운 데이터셋 $D=(x^{(i)}, y^{(i)})^n_{i=1}$이 있다고 하자. 경험적 에러는 단순하게 $f(x^{(i)})$ 가 실제 라벨 $y^{(i)}$와 일치하지 않는 비율로 볼 수 있기 때문에 아래와 같은 식으로 표현한다.

이와 대조적으로 반면 모집단 에러는 기본 모집단에서 분류기가 실제 레이블과 일치하지 않는 예시 중 예상되는 비율이다. (P(X,Y)의 확률 밀도함수 p(x,y))

다만, 위 수식에서 $\epsilon (f)$는 실제로 특정할 수 없고 샘플 데이터를 기반으로 추정할 수 있을 뿐이다. 테스트 셋이 사실상 기본 모집단을 통계적으로 대표하기 때문에 $\epsilon \mathcal D(f)$가 집단 오차의 통계적 추정치로 볼 수 있다. 즉, 간단하게 평균추정의 문제로 볼 수 있다.

중심극한정리(central limit theorem)은 어떤 분포에서든 평균 $\mu$와 표준편차 $\sigma$를 가진 n개의 무작위 샘플을 가지고 있을 때, 샘플 수 n이 무한대에 가까워질수록 샘플 평균이 실제 평균을 중심으로 하는 정규분포에 접근한다는 것을 보장한다. (표준편차는 $\sigma / \sqrt{n}$) 이는 예제가 많아질수록 테스트 에러 $\epsilon \mathcal D(f)$는 실제 에러 $\epsilon(f)$에 $\mathcal O(1 / \sqrt{n})$의 비율로 가까워진다는 것을 알려준다.

앞서 랜덤 변수 $1(f(X) \neq Y)$는 0과 1만 취할 수 있으므로 Bernoulli 랜덤 변수이다. 여기서 1은 분류기가 오류를 일으켰음을 의미하므로 랜덤 변수의 매개 변수는 실제 오류율이다. 이때, 분산 $\sigma^2$은 $\epsilon(f)(1-\epsilon(f))$ 수식 표현에 의존한다. 이 함수를 조금만 조사해 보면 실제 오차율이 0.5에 가까울 때 분산이 가장 높고, 0에 가깝거나 1에 가까울 때 훨씬 낮아질 수 있음을 알 수 있다. 이러한 사실은 오차 추정치의 점근 표준 편차가 $\sqrt{0.25/n}$보다 클 수 없다는 것을 의미한다.

테스트 오류를 모집단 오류와 0.01의 표준편차 내에서 근사하게 하려면, 표준편차의 공식을 사용하여 샘플 크기를 결정할 수 있다. $\sigma / \sqrt{n}$에서 0.01이 되도록하는 n을 찾을 때 대략 2500개의 샘플이 필요하며, 95%(0.005)의 신뢰도로 하려면 약 10,000개의 샘플이 필요하다.

중심극한정리는 무한 샘플에 대한 관계를 설명하지만, Hoeffding의 부등식을 사용하여 유한 샘플에 대한 유효한 경계를 얻을 수 있다.

동일하게 95%의 신뢰도로 추정치와 실제 오차율 사이의 거리 t가 0.01을 초과하지 않기 위해서는 위의 분석에서 제안한 10,000개의 예시와 비교하여 약 15,000개의 예시가 필요하다는 것을 알 수 있다.

2) Test Set Reuse

거의 모든 실용적인 모델들은 테스트 세트 성능을 기반으로 개발되고 검증된다.

새로운 모델을 훈련할 때, 분류기의 오류율에 대한 확신이 필요하므로, 적절한 수의 예제를 테스트 세트로 결정한다. 테스트 세트의 무결성을 유지하기 위해 모든 예비 분석, 하이퍼파라미터 조정 및 여러 모델 아키텍처 선택을 검증 세트에서 수행했다고 가정하자. 마지막으로 테스트 세트에서 모델 f1을 평가하고, 관련 신뢰구간과 함께 모집단 오차에 대한 편향되지 않은 추정치를 기록했다고 하자.

그런데, 모델링 접근 방식에 대한 기발한 아이디어가 떠올라 새 모델을 코딩하고 검증 데이터 세트에서 하이퍼파라미터를 조정한 결과 오류율이 기존 모델에 비해 낮아졌다. 하지만, 새로운 모델에 적합한 테스트 세트가 없다. 이게 왜 문제일까?

두 가지 심각한 문제에 직면하게 된다.

첫째, 테스트 집합을 수집할 때는 단일 분류기를 평가한다는 가정 하에 필요한 정확도 수준을 결정했다. 그러나, 동일한 테스트 세트에서 여러 분류기를 평가하면 false discovery문제를 고려해야 한다. 예를 들어, 이전에는 95%의 확신을 가졌기 때문에 잘못된 결과가 나올 확률은 5%에 불과했지만, 여러 개인 경우 테스트 성능이 잘못된 분류기가 하나도 없다고 보장하기 어렵다.

다음으로, 최종 평가에서 얻을 결과를 신뢰할 수 없다. 테스트 세트 성능에 대한 분석은 분류기가 테스트 세트와 접촉하지 않고 선택되어 테스트 세트가 기본 모집단에서 무작위로 추출된 것으로 볼 수 있다는 가정을 전제로 했다는 점을 기억할 것이다. 현재, 기존 모델의 테스트 세트 성능을 관찰한 후 후속 함수 f2를 선택했다. 이후부터는 모델러에게 테스트 집합의 정보가 일부 유출되었다고 볼 수 있으므로 진정한 테스트 집합이라고 부를 수 없다. 이러한 문제를 adaptive overfitting이라고 한다.

따라서, 실제 머신러닝 프로젝트에서는 테스트 세트를 실제 환경을 반영하도록 신중하게 생성해야 하며 테스트 세트는 가능한 한 적게 참조해야 한다. 벤치마크 챌린지를 실행할 때는 여러 테스트 세트를 유지하는 것이 좋다. 각 라운드 후에 이전 테스트 세트는 검증 세트로 만들고, 새로운 테스트 세트에 대해 모델을 평가할 수 있도록 한다.

3) Statistical Learning Theory

테스트 세트는 우리가 가지고 있는 가장 확실한 평가 도구이지만, 여러 한계를 가지고 있다. 우리가 직접 데이터셋을 만들지 않는 한, 진정한 테스트 세트를 가지고 있기는 어려우며, 진정한 테스트 세트가 있더라도 이는 단지 분류기가 모집단에 일반화되었는지 여부를 사후적으로만 알려줄 뿐, 사전적으로 일반화될 것이라고 기대할 수 있는 이유를 제공하지 않는다.

통계적 학습 이론은 이러한 한계를 극복하고자 하는 수학적인 분야로, 모델이 언제 어떻게 일반화될 수 있는지에 대한 근본적인 원리를 밝히려고 한다. 이 분야의 주요 목표 중 하나는 모델 클래스의 특성과 데이터셋의 샘플 수에 따라 일반화 간격을 제한하는 것이다.

학습 이론가들은 훈련 집합 $S$에서 훈련되고 평가된 학습된 분류기 $fs$의 경험적 오차 $\epsilon s(fs)$와 기본 모집단에서 동일한 분류기의 실제 오차 $\epsilon(fs)$ 사이의 차이를 제한하는 것을 목표한다. 이전에는 분류기 $f$가 고정되어 있었고 평가 목적으로만 데이터 세트가 필요했다. 그리고 실제로 고정된 분류기는 일반화된다. (에러는 unbiased estimate of the population error) 하지만 동일한 데이터 세트에 대해 분류기를 학습시키고 평가할 때는 어떻게 해야 할까? 훈련 오차가 테스트 오차에 근접할 것이라고 확신할 수 있을까?

$fs$가 미리 지정된 함수 $F$에서 선택되어야 한다고 가정하자. 앞서, 단일 분류기의 오차를 추정하는 것은 쉽지만, 여러 분류기를 고려할 때 상황이 복잡해지는 것을 기억할 것이다. 설령, 하나의 분류기의 경험적 오차가 높은 확률로 실제 오차에 가깝다고 하더라도 말이다. 잘못된 분류자를 선택하게 되면, 모집단 오차를 지나치게 과소평가할 수 있다. 선형 모델의 경우에도 매개 변수의 값이 연속적이기 때문에 일반적으로 무한한 클래스 함수 중에서 선택하게 된다.

이러한 문제에 대한 한 가지 해결책은 균일 수렴(uniform convergence), 즉 높은 확률로 클래스 $f \in \mathcal F$에 속하는 모든 분류기의 경험적 오류율이 실제 오류율로 수렴한다는 것을 증명하기 위한 분석 도구를 개발하는 것이다. 다시 말해, 적어도 $1-\delta$의 높은 확률로 $f$ 클래스의 모든 분류기 중 어떤 분류기의 오류율 $\epsilon(f)$도 작은 $\alpha$보다 더 많이 잘못 추정되지 않을 것이라 말할 수 있는 이론적 원리를 찾는 것 이다. 그러나 이러한 주장은 모든 모델 클래스에 대해 가능한 것도 아니다. 예를 들어, 앞선 질문으로 나왔던 경험적 오류가 없지만 기본 모집단에서 무작위 추측보다 나은 성능을 내지 못하는 암기 모델 클래스를 떠올려볼 수 있다.

어떤 의미에서 이런 암기 모델 클래스는 너무 유연하다. 반면에 고정 분류기는 완벽하게 일반화하지만 훈련 데이터나 테스트 데이터에 모두 맞지 않는 쓸모없는 분류기이다. 유연한(변동성이 높은) 모델 클래스는 훈련 데이터에는 더 잘 맞지만 과적합(overfitting)의 위험이 있고, 덜 유연한(편향이 높은) 모델 클래스는 일반화는 잘하지만 과소적합(underfitting)의 위험이 있다. 학습 이론에서 중요한 질문 중 하나는 모델이 이 스펙트럼 상에서 어디에 위치하는지를 수량화하고 관련 보장을 제공하는 적절한 수학적 분석을 개발하는 것이다.

Vanpik과 Chervonenkis는 상대 빈도의 수렴에 관한 이론을 보다 일반적인 함수 클래스로 확장했다. 이 작업의 주요 공헌 중 하나는 모델 클래스의 복잡성(유연성)을 측정하는 개념인 Vapnik-Chervonenkis(VC) 차원이다. 다음으로, 중요한 결과 중 하나는 VC 차원과 표본 수의 함수로 경험적 오차와 모집단 오차 간의 차이를 제한하는 것이다.

• 기호 정의 $P$: 확률 $R[p,f]$: $f$에 대한 실제 오류율(일반화 오류율) $R_{emp}[X,Y,f]$: $f$에 대한 경험적 오류율 $\alpha$: 일반화 갭한 $\delta>0$: 바운드를 위반할 확률 $c>0$: 발생할 수 있는 손실의 규모에만 의존하는 상수 $VC$: VC차원, 모델의 복잡성을 측정하는 지표 $n$: 표본의 크기
  

앞서 우리는 일반화 오류와 경험적 오류의 차이를 줄이고자 했다. 이 수식의 용도는 원하는 델타 및 알파 값을 입력하여 수집할 샘플 수를 결정하는 것이다.

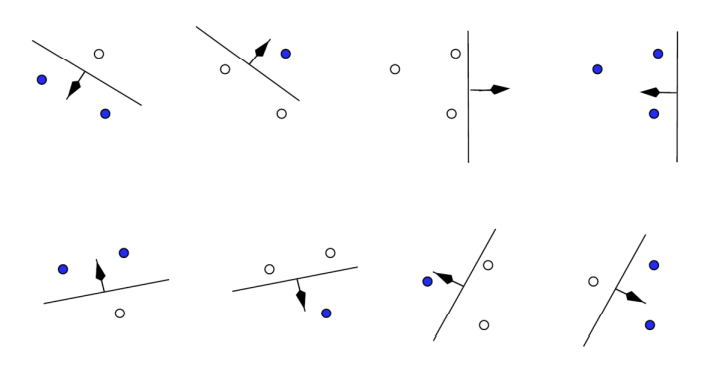
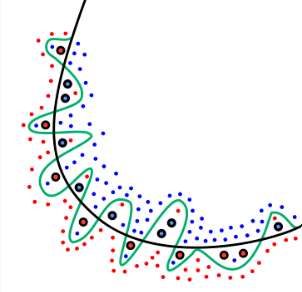
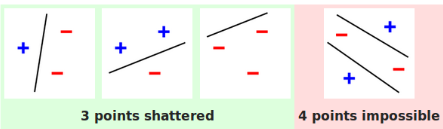
다음으로 VC차원에 대해 이해하기 전 Shattering에 대해 이해해야 한다. Shattering는 분류기가 데이터 세트의 모든 점에 대해 가능한 모든 이진 레이블링을 정확하게 분류할 수 있는 능력을 의미한다. 즉, 이는 분류기가 해당 데이터 세트에 존재하는 모든 패턴을 완벽하게 학습할 수 있음을 나타낸다. 아래 그림의 경우 3개의 점을 하나의 직선이 모두 분류할 수 있으므로 Shatter 한다고 말한다. 분류기가 더 많은 점들을 Shatter할 수 있다면, 그만큼 더 복잡하고 유연하다고 할 수 있다.

(https://prod-files-secure.s3.us-west-2.amazonaws.com/d6e6721b-69cf-433a-8992-1ffb48554d2b/5c278360-f3b6-46c5-900e-7b85acb3f34c/Untitled.png)

VC 차원은 shattering과 밀접하게 관련되어 있다. VC 차원은 분류기의 복잡성을 나타내는 지표로, 분류기가 어떤 데이터 세트를 완전히 ‘Shatter'할 수 있는 최대 크기를 말한다. (혹은 Capacity를 측정한 지표라고도 한다.) 구체적으로, $n$개의 점들에 대해 가능한 모든 $2^n$레이블링을 분류기가 정확하게 분류할 수 있다면, 그리고 $n+1$개의 점들에 대해서는 어떤 레이블링 조합에 대해서라도 분류기가 완벽하게 분류하지 못한다면, 분류기의 VC차원은 $n$이다. 앞선, 2 차원 상에 있는 직선 분류기의 VC 차원의 값은 3이다.

If you can find a set of $n$ points, so that it can be shattered by the classifier (i.e classify all possible $2^n$ labeling correctly) and you cannot find any set of $n+1$ points that can be shattered (i.e for any set of $n+1$ points there is at least one labeling oreder so that the classifier can not separate all points correctly), then the VC dimension is $n$.

What is the exact definition of VC dimension?

https://minye-lee19.gitbook.io/sw-engineer/business-analytics/class/2-1-svm

즉, VC 차원이 클 수록 높은 Capacity를 가진 모델이라 볼 수 있다. 이는 더 복잡한 패턴을 학습하고 예측할 수 있지만, 동시에 과적합(overfitting)의 위험이 커질 수 있다. 반대로, 낮은 Capacity를 가진 모델은 더 단순하고 일반화에 더 강하지만, 복잡한 패턴을 포착하는 데는 제한적일 수 있다. (높은 VC 차원은 일반적으로 높은 표현력과 유연성을 의미하지만, 항상 더 나은 성능을 보장하는 것은 아니다.)

또한, 위 수식에 따른 이론은 더 복잡한 모델에 대해서 이 보장을 얻으려면 일반적으로 원하는 오류율을 달성하는 데 실제로 필요한 것보다 훨씬 더 많은 예제가 필요하다. 더군다나, 모델 클래스와 $\delta$를 고정하면, 오차율은 다시 일반적인 $\mathcal O(1/\sqrt(n))$비율로 감소한다.

최근 딥러닝과 같은 VC 차원이 높더라도 다양한 과적합 방지 기법들이 존재해, 이론이 위협받고 있다고 한다. Deep neural network의 경우 수백만 개 이상의 매개변수를 가지고 있으며, 대규모 포인트에 무작위 레이블을 쉽게 할당할 수 있지만, 실제 문제에서 일반화를 잘 수행하며, 놀랍게도 더 크고 깊은 문제일수록 더 높은 VC 차원이 발생함에도 불구하고 더 잘 일반화되는 경우가 많다.

7. Environment and Distribution Shift

@Tommy Kim

많은 개발자들이 개발할 때, 모델에만 집중하지만, 개발자들은 단순히 기술적인 측면뿐만 아니라, 모델이 적용되는 환경, 데이터의 출처 및 품질, 그리고 모델의 결정이 가져올 장기적인 사회적, 윤리적 영향 등을 종합적으로 고려해야 한다. 모델이 실제 세계에 적용될 때 발생할 수 있는 예상치 못한 결과와 그에 따른 부작용을 이해하고, 이를 미연에 방지하기 위한 적절한 조치를 취하는 것이 중요하다.

1) Types of Distribution Shift

train data가 어떤 분포 P에서 추출되었지만, test data는 분포 Q에서 추출되어서 label에 존재하지 않는 예시들로 구성되었다고 가정해보자. 분포 P와 Q가 어떠한 연관도 없다면 robust한 분류 모델을 학습하는 게 불가능해진다.

예를 들어, 이진 분류 문제에서 개와 고양이를 분류하는 상황을 가정해보자. 우리는 입력 분포가 일정하다는 가정을 통해 예측을 하지만, $P(x) = Q(x)$, 신이 갑자기 앞으로 모든 고양이를 개로, 모든 개를 고양이라고 정정한다면, 우리는 이러한 극단적으로 출력 분포가 뒤바뀌는 상황을 감지해내지 못한다.

이에 따라 데이터가 미래에 어떤식으로 변할지에 대한 제한된 가정 하에, 분류기의 정확도를 개선하는 방법들이 연구되었다.

a. Covariate Shift

공변량 변화(covariate shift)는 입력 데이터의 분포 $P(X)$는 시간에 따라 변할 수 있지만, label의 값을 결정하는 조건부 확률 $P(Y|X)$는 변하지 않는다고 가정한다.

예를 들어, 다음과 같이 개와 고양이를 구별하는 문제가 있다고 가정하자.

위의 실제 개와 고양이 사진들로 학습한 분류 모델을 만들었다고 하자. 실제 test data는 다음과 같다.

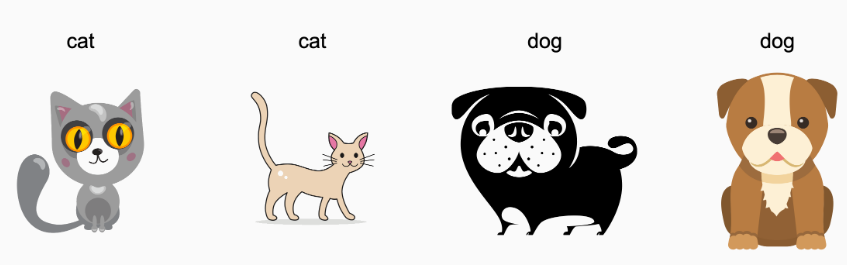
이렇게 사진 이미지(입력)을 통해 개와 고양이를 구별하는 문제($P(Y|X)$)임에는 변함이 없지만, 입력 분포가 만화 이미지로 변함에 따라, 새로운 도메인에도 적용되는 로직이 없다면, 분류 모델이 robust하게 분류하기는 불가능할 수 있다.

b. Label Shift

label shift는 label로부터 입력 $X$가 추론될 때 발생하는 문제를 다룬다 : ex) 질병에 따른 증상. 여기서 label의 분포 $P(Y)$는 변할 수 있지만, 조건부 확률 분포 $P(X|Y)$는 변하지 않는다고 가정한다.

예를 들어, 증상에 따라 질병을 진단하는 문제를 다룬다고 가정해보자. 시간이 지남에 따라 질병의 발병률 : ex ) 코로나 발병률 등은 변할 수 있지만, 질병에 따른 증상들은 변하지 않는 것이 label shift의 가정이다.

한 가지 흥미로운 점은, $P(Y|X)$가 유지 되는 상황이 만족한다면, label shift와 covariate shift는 동시에 적용될 수 있다. 두 shift가 모두 만족되는 상황이라면, label shift를 채택하는 것이 자연스럽. 딥러닝의 문제에서 label은 입력 feature $X$에 비해 차원이 훨씬 적기 때문에, label을 다루는 것이 현명하기 때문이다.

c. Concept Shift

concept shift란 label의 정의 자체가 시간이 지남에 따라 변화할 수 있는 상황을 의미한다. 정신 질환의 진단 기준, 유행하는 패션, 직업 명칭 등의 변화가 모두 concept shift에 해당한다.

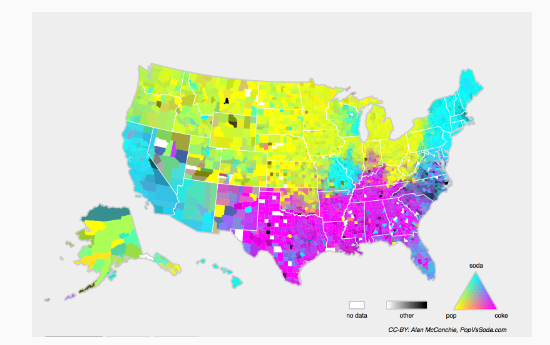
위 그림은 미국 전역에서 탄산 음료를 부르는 명칭의 분포를 나타낸다. 지역별로 탄산 음료를 부르는 명칭이 다르기 때문에 ,위치에 따라 조건부 확률 $P(Y|X)$가 달라질 수 있다. 이러한 이유로 모델을 설계할 때, 현실 세계의 동적인 상황에 잘 대응할 수 있도록 설계해야 한다.

2) Examples of Distribution Shift

a. Medical Diagnostics

암을 탐지하는 알고리즘을 개발하기 위해 건강한 사람들과 아픈 사람들로부터 데이터를 수집하고 모델을 훈련시킨다고 해보자. 모델이 아무리 잘 준비가 되었다고 하더라도, 실제 환경의 데이터 분포는 상당히 다를 수 있다.

예를 들어, 한 스타트업에서 나이든 남성에게 영향을 미치는 질병에 대한 혈액 검사 모델을 개발하려고 했다. 문제는, 건강한 남성들로부터 혈액 샘플을 얻기가 어려워서 데이터 간의 분포의 차이가 발생하였다. 건강한 남성의 데이터를 얻기 위해 대학 캠퍼스에서 학생들로부터 혈액을 기증 받았지만, 건강이 나쁜 나이든 남성들과는 연령, 호르몬 수치, 신체 활동, 식습관, 알코올 소비 등 여러가지가 달라져서 covriate shift가 발생했다. 이에 따라, 훈련 데이터와 실제 데이터 간에 상당한 차이가 생겨서 교정하기가 어려운 문제가 있었다.

b. Self_Driving Cars

자율 주행 자동차를 만드려고 한 노력이 있었는데, 실제 주행 데이터를 가져오는 것은 힘들어서, 게임 내부의 도로 데이터를 통해 추가 학습한 결과, 게임 랜더링 엔진을 통해 얻어진 ‘test data’는 비교적 잘 작동하는 모습을 보여주었지만, 게임 내부 도로는 매우 단순한 텍스처로 랜더링되어 있었기 때문에 실제 환경의 주행에서의 결과는 처참하였다.

c. Nonstationary Distributions

데이터의 분포가 느리게 변화하는 경우(비고정 분포라고도함)에 모델이 적절하게 업데이트 되지 않는 경우, 몇 가지 좋지 못한 상황이 발생할 수 있다.

• 컴퓨터 화면에 띄워지는 광고 모델을 학습 시킨 후에 자주 업데이트 하지 않으면, 신형 전자기기의 출시를 광고하지 못할 수 있다.
• 스팸 필터를 잘 구축해도, 스팸 발송자들은 지금까지 본 적이 없는 새로운 메시지를 끊임없이 만들어낸다.
• 제품 추천 시스템을 만들어 놓고 업데이트 하지 않으면, 크리스마스가 지난 후에도 산타 모자를 계속 추천할 수 있다.

d. More Anecdotes

• 얼굴 감지기를 만들고 성능을 확인하는데, training data에 없던 이미지가 발견되면 test data는 잘 작동하지 않을 수 있다.
• 미국 시장용 웹 검색 엔진을 구축하여 영국에 배포하려고 하는 경우, 변화된 데이터 분포에 잘 대응해야 한다.
• 대규모 데이터 셋(1000개의 카테고리, 각 카테고리마다 1000개의 이미지)를 학습 시킨 이미지 분류 모델을, 실제 label 분포가 균일하지 않은 실제 환경에 배포되는 경우

3) Correction of Distribution Shift

@w2y

a. Empirical Risk and Risk

• Empirical risk(경험적 위험)
  : (실제)‘Risk’와 근사화하기 위한 train data에 대한 평균 손실

• Risk
  : 실제 $p(\bold{x}, y)$ 분포에서 추출된 전체 데이터 모집단에 대한 손실 기댓값

일반적으로 전체 데이터셋을 얻을 수 없기 때문에, empirical risk를 최소화함으로써 실제 risk를 대략적으로 최소화한다.

b. Covariate Shift Correction

Source distribution $q(\bold{x})$, Target distribution $p(\bold{x})$

각 샘플 $(\bold{x}_i, y_i)$에 대한 $\beta_i$를 곱해줌(확률 비율로 샘플 reweight)으로써 ‘weighted empirical risk minimization’을 통해 모델을 학습할 수 있다.

하지만 실제 $p$를 알 수 없기 때문에 source distribution($q$)와 target distribution($p$)에서 샘플을 뽑아 logistic regression으로 이중 분류기(binary classifier)를 학습시켜 함수 $h$를 구한다. 이를 적용하여 weight($\beta_i$)를 다음과 같이 정의할 수 있다.

c. Label Shift Correction

d. Concept Shift Correction

• Concept Shift(개념 전환) : 고양이와 개를 구별하는 것에서 흰색과 검은색 동물을 구별하는 것으로 바뀌는 상황

새롭게 데이터를 수집하고 처음부터 훈련하는 것보다 모델을 훨씬 더 잘 수정시키는 것은 비합리적이다.

일반적으로는, 새로운 제품이 출시되어 오래된 제품의 인기가 점진적으로 떨어지는 것처럼 천천히 변화가 생긴다. 이에 따른 상품 클릭률 예측도 점진적으로 변해야한다. 이러한 경우, 처음부터 훈련하는 대신 기존 네트워크 가중치를 가지고 새 데이터로 조금 업데이트 하면 된다.

4) A Taxonomy of Learning Problems

@Tommy Kim

a. Batch Learning

batch learning은 off-line learning이라고도 불리며, 가용한 모든 데이터를 전부 활용해서 모델을 학습 시킨 후에 배포하고, 더 이상 업데이트 하지 않는 것을 말한다. 예를 들어, 개와 고양이를 분류하는 모델을 만들 때 사용할 수 있는 모든 데이터를 전부 활용하고, 훈련이 완료되면 고양이만 출입할 수 있는 스마트 캣도어 시스템을 만들 수 있다. 이 시스템은 고객들의 집에 설치한 후에는, 다시는 업데이트 되지 않는다.

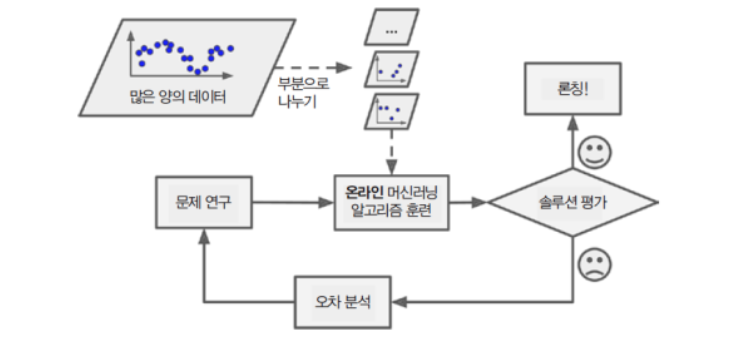
b. Online Learning

온라인 학습은 batch-learning과 반대로 시간이 지남에 따라 새로운 데이터들이 생성되고, 이에 따라 모델을 업데이트 해나가는 방식이다. 현실의 많은 문제가 online learning에 속하는데, 주가의 경우에 매일 주가 데이터가 갱신되고, 우리는 이를 바탕으로 모델을 업데이트할 수 있다.

c. Bandits

bandits 문제는 bandit(슬롯 머신)에서 유래된 문제인데, 각 단계에서 슬롯 레버를 당겼을 때, 얻게 되는 보상들의 합을 최대화 하는 문제이다. 이는 강화 학습과 비슷한 면을 보이지만, 강화 학습과는 다르게 agent의 행동에 따라 환경이 변하지 않는다.

d. Control

개발자들이 만든 모델 및 시스템이 취하는 행동마다 환경(environment)는 달라지게 된다 : ex) 커피 보일러에서 이전에 가열이 되었는지 여부에 따라 온도(환경)이 달라짐. 이에 따라 PID 제어 이론 및 추천 시스템 등 환경의 변화 요소 까지 고려하여 제어하는 노력이 더해지고 있다.

e. Reinforcement Learning

우리는 메모리에 저장되는 환경에 더 일반적이 상황을 만나게 될 수 있다. 환경과 협업하는 경우(non-zerosum : 협동 게임)와 환경과 적대적인 경우(체스, 바둑, 스타크래프트)가 대표적인 예이다. 이런 상황에서 최적의 행동을 하도록 모델을 만드는 것을 강화 학습이라고 부른다. 자율 주행의 경우에도 다른 자동차의 주행 스타일에 따라 피하거나, 추월하는 등의 알고리즘을 만들 수 있다.

f. Considering Environment

알고리즘 및 모델을 개발할 때, 환경이 변화하는 속도 및 방식을 고려해야 한다. 환경이 느리게 변하지만, 확실하게 변한다면, 이에 대한 모델을 전반적으로 개편해야 하고, 급격하게 변하지만, 매우 드문 현상이라면 이를 수용하고 모델 변경을 하지 않을 수도 있는 것이다.

5) Fairness, Accountability, and Transparency in Machine Learning

@리치

머신러닝 시스템을 구축할 때는 단순히 예측 모델을 최적화 하는 것 이상의 일을 하는 것임을 기억해야 한다. 이러한 시스템은 결정을 자동화하는 도구로 사용되는데, 그 결과로 발생하는 결정에 의해 영향을 받는 개인들의 삶에 영향을 줄 수 있다. 예측에서 결정을 내리는 것으로 넘어가면서, 새로운 기술적 질문 뿐만 아니라 신중하게 고려해야 할 윤리적 질문들도 고려해야 한다.

예를 들어, 의료 진단 시스템을 배포할 때 어떤 인구 집단에 대해 효과가 있을지 알아야 한다. 예측 가능한 위험을 간과할 경우 좋지 않은 치료를 시행할 수 있기 때문이다. 또한, 의사 결정 시스템을 고려할 때는 평가 방법을 재고해야 한다. 왜냐하면, 정확도가 올바른 척도가 되는 경우가 드물기 때문이다. 대표적으로 이미지를 잘못 분류하는 한 가지 방법이 인종 차별로 인식될 수 있는 반면, 다른 카테고리로 잘못 분류하는 것은 무해하다면, 의사 결정 프로토콜을 설계할 때 사회적 가치를 고려하여 적절히 조정할 수 있다.

Twitter, https://www.aitimes.com/news/articleView.html?idxno=132361

범죄가 많이 발생할 것으로 예상되는 지역에 순찰 경찰관을 배치하는 예측 치안 시스템을 생각해보자.

1. 범죄가 많이 발생하는 지역은 더 많은 순찰을 받게 된다.
2. 결과적으로 이런 지역에서 더 많은 범죄가 발견되어 향후 반복 학습에 사용할 수 있는 훈련 데이터에 입력된다.
3. 더 많은 양의 범죄에 노출된 모델은 이 지역에서 다 많은 범죄가 발생할 것으로 예측한다.
4. 업데이트 된 모델이 해당 지역을 다시 집중하여 더 많은 범죄를 발견하는 과정을 거치게 된다.

이 예제에서 알 수 있듯이 모델의 예측이 학습 데이터와 결합되는 다양한 메커니즘이 모델링 과정에서 고려되지 않는 경우가 많다. 이런 현상을 ‘Runaway Feedback Loop’ 이라 부른다. 또한, 애초에 올바른 문제를 해결하고 있는지 주의해야 한다. 예측 알고리즘은 이제 정보의 전달을 중재하는 데 있어 중요한 역할을 맡고 있다. “Facebook에서 개인이 접하는 뉴스가 ‘좋아요’ 누른 페이지의 집합에 따라 결정되어야 할까?” 는 가장 대표적으로 직면할 수 있는 윤리적 딜레마다.