2.1 Data Manipulation

데이터의 중요한 2가지 (i) 데이터 획득, (ii) 데이터 처리

데이터 처리에서 중요한 MXNet의 ndarray와 PyTorch 와 TensorFlow의 Tensor

Tensor는 differentiation 지원
NumPy는 CPU에서 지원되지만, Tensro class는 GPU를 활용 -> Neural Networks에 적합

import torch 
# only one axis is needed, a tensor is called a vector
# With two axes, a tensor is called a matrix ( k^th-order tensor )

x = torch.arange(12, dtype=torch.float32) 
# tensor([ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10., 11.])

x.numel() # 12

기존 shape (12,)에서 (3,4)로도 변경할 수 있음

X = x.reshape(3, 4)
tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11.]])
        
# 사이즈를 모른다면 x.reshape(-1,4) or x.reshape(3,-1)

생성은 0 / 1 / Random 으로 할 수 있다. 당연하게도, 여러개의 숫자로 각 원소에 대한 값을 지정할 수 있다.

torch.zeros((2,3,4))
torch.ones((2,3,4)) 
torch.randn(3,4) 

torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])

Indexing과 Slicing은 NumPy와 유사하다. ex) X[start:stop] , 이때 stop에 해당하는 인덱스는 반환되지 않는다.

아래 코드처럼 한번에 특정 범위의 값을 모두 변경할 수 있다.

X[:2, :] = 12 # 처음과 두번 째 행의 모든 원소를 12로 변경 
tensor([[12., 12., 12., 12.],
        [12., 12., 12., 12.],
        [ 8.,  9., 10., 11.]])

tensor는 각 원소에 특정 operation을 적용할 수 있다. 벡터 처럼 연산도 가능하다.

torch.exp(x) 

x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
x + y, x - y, x * y, x / y, x ** y # 벡터 연산 

두 개의 tensor를 rows로 합치거나, columns으로 합칠 수 있다.

X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)

차원이 다른 두 tensor도 연산할 수 있다.

(tensor([[0],
         [1],
         [2]]),
 tensor([[0, 1]]))
 a + b 
 tensor([[0, 1],
        [1, 2],
        [2, 3]])

Broadcasting 방법은 두 차원을 비교하여 차원을 늘린 뒤 더한다.
(3,1) -> (3,2) 그리고 행을 복사
(1,2) -> (3,2) 그리고 열을 복사

기존 파이썬은 불필요한 메모리 낭비가 있다. 머신 러닝에서 수백개의 파라미터를 매번 업데이트할 때 메모리 낭비가 심해진다. 또한, 오래된 파라미터를 참조할 가능성도 있다. Tensor는 이를 해결함.

더불어, NumPy와 타입 변환이 쉽다.

2.2 Data Perprocessing

Pandas 라이브러리를 많이 사용한다. 보통 CSV라 부르는 파일을 사용한다. (쉼표로 값이 구분된다고 하여 Comma-separated values)

import pandas as pd
data = pd.read_csv(data_file)

iloc을 활용하여, 특정 정수 위치에 접근도 가능하다. 또한, 결측치 Nan에 대한 처리도 가능하다.

data.iloc[:, 0:2] # 모든 행에서 0:2에 해당하는 열 

data.iloc[:, 2] # 모든 행에서 2에 해당하는 열 

data.fillna(x) # x로 결측치 대체

2.3 Linear Algebra

$x \in \R$ 이 scalar를 공식적으로 표현하는 방법 , 앞서 말했듯 원소가 하나인 tensor

벡터는 스칼라의 고정 길이 배열, 1-st order tensors (원소를 수직으로 쌓으면 벡터), $x \in \R^n$

행렬은 2-nd order tensors, $A \in \R^{m*n}$
행과 열을 바꾸는걸 Trnaspose라 부름 $B = A^T$ then $b_{ij} = a _{ji}$

Tensro에 관한 기본 연산

B = A.clone()  # Assign a copy of A to B by allocating new memory
A * B # Hadamard product: elementwise product of two matrices
x.sum() #  the sum of a tensor’s elements, reduction!
A.shape, A.sum(axis=0).shape # (torch.Size([2, 3]), torch.Size([3]))

sum_A = A.sum(axis=1, keepdims=True) # Non-reduction sum 
A.cumsum(axis=0) # cumulative sum 

torch.dot(x, y) # x^Ty, dot products
torch.sum(x * y)

torch.mv(A, x), A@x # matrix–vector product
torch.mm(A, B), A@B # matrix–matrix multiplication

아래 3가지 성질을 만족하는 함수를 Norm이라 부른다.

1. 주어진 임의의 벡터에 대해, 만약 스칼라 값으로 벡터의 모든 요소를 scale했을 때, 그 벡터의 norm 또한 스케일에 따라 변한다. $||\alpha x|| = |\alpha|||x||$

2. 어떤 벡터 x와 y에 대해서 norm은 triangle inequality를 만족한다. $||x+y|| <= ||x|| + ||y||

3. 벡터의 norm은 항상 0 또는 양수 값이며, 오직 그 벡터가 영 벡터(zero vector)일 때만 0이다. $||x|| > 0$ for all x !=0

$l_2$ norm: $||x||_2 = \sqrt{\Sigma_{i=1}^n x_i^2}$
$l_1$ norm: $||x||_1 = \Sigma_{i=1}^n |x_i|$

이는 $l_p$ norm의 스패셜 케이스이다.
$||x||_p = (\Sigma_{i=1}^n |x_i|^p)^{1/p}$

torch.norm(u) # l2 
torch.abs(u).sum() # l1

• Frobenius norm

2.4 Calculus

기본 미적분학 수식을 코드로 작성

%matplotlib inline
import numpy as np
from matplotlib_inline import backend_inline
from d2l import torch as d2l

def f(x):
    return 3 * x ** 2 - 4 * x
    
for h in 10.0**np.arange(-1, -6, -1):
    print(f'h={h:.5f}, numerical limit={(f(1+h)-f(1))/h:.5f}')

시각화 하는 방법

def use_svg_display():  #@save # d2l 패키지에 저장하여 나중에 코드를 반복하지 않고 호출할 수 있도록 하는 특수 수정자
    """Use the svg format to display a plot in Jupyter."""
    backend_inline.set_matplotlib_formats('svg')

def set_figsize(figsize=(3.5, 2.5)):  #@save
    """Set the figure size for matplotlib."""
    use_svg_display()
    d2l.plt.rcParams['figure.figsize'] = figsize
    
#@save
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
    """Set the axes for matplotlib."""
    axes.set_xlabel(xlabel), axes.set_ylabel(ylabel)
    axes.set_xscale(xscale), axes.set_yscale(yscale)
    axes.set_xlim(xlim),     axes.set_ylim(ylim)
    if legend:
        axes.legend(legend)
    axes.grid()

#@save
def plot(X, Y=None, xlabel=None, ylabel=None, legend=[], xlim=None,
         ylim=None, xscale='linear', yscale='linear',
         fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
    """Plot data points."""

    def has_one_axis(X):  # True if X (tensor or list) has 1 axis
        return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)
                and not hasattr(X[0], "__len__"))

    if has_one_axis(X): X = [X]
    if Y is None:
        X, Y = [[]] * len(X), X
    elif has_one_axis(Y):
        Y = [Y]
    if len(X) != len(Y):
        X = X * len(Y)

    set_figsize(figsize)
    if axes is None:
        axes = d2l.plt.gca()
    axes.cla()
    for x, y, fmt in zip(X, Y, fmts):
        axes.plot(x,y,fmt) if len(x) else axes.plot(y,fmt)
    set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)

x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])

편미분

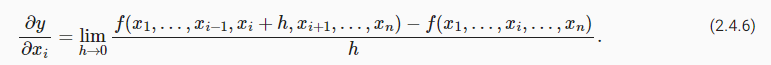
$x_i$를 제외하고 모두 constant로 생각

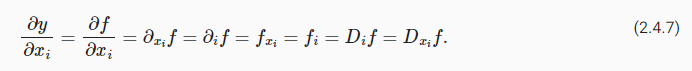
x에 대한 함수 f의 gradient는 벡터 n의 partial derivatives이다.

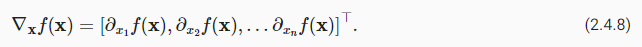
아래 특징이 있다.

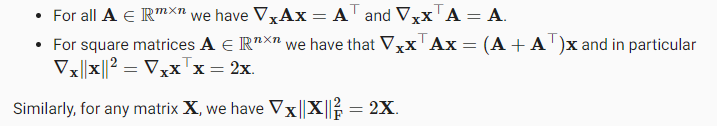
Chain rule
$y=f(u), u=g(x)$

$y=f(u)$가 $u_1,u_2,...,u_m$ where each $u_i=g_i(x)$ 이고, $x_1,x_2,...,x_n$

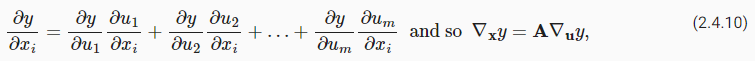
$A \in \R^{n*m}$, A는 벡터 x에 대한 벡터 u의 미분을 포함하는 행렬

2.5 Automatic Differentiation

Backpropagation을 모른다면 https://wikidocs.net/37406에서 읽어보는 것을 추천합니다.

현대의 딥러닝 프레임워크들은 모두 Autograd를 제공한다. 이는 결국 backpropagation 계산을 위해 존재한다고 봐도 될 것 같다.

$y=2x^Tx$ 함수가 있고, x는 column vector라고 하자.

# Can also create x = torch.arange(4.0, requires_grad=True)
x.requires_grad_(True) 

requiresgrad(True)는 이 tensor 대한 연산을 추적하여 자동으로 gradient를 계산하도록 설정한다. 이는 x가 신경망에서 가중치와 같은 학습 가능한 파라미터임을 나타낸다.

y = 2 * torch.dot(x, x) # tensor(28., grad_fn=<MulBackward0>)

y.backward()
x.grad

y에 대한 그래디언트를 계산하는 backpropagation, x에 대한 y의 미분 값을 계산하고, 이를 x.grad에 저장한다.

Jacobian: 벡터 y에 대한 벡터 x의 미분, y의 각 구성 요소에 대해 x의 각 구성 요소에 대한 편미분을 포함(?)

Non-scalar에 대한 gradient를 계산할 때, PyTorch와 같은 딥러닝 프레임워크는 혼란을 방지하기 위해 backward를 호출할 때, PyTorch는 객체를 스칼라로 축소하는 방법을 지정하지 않으면 오류를 발생시킨다. 즉, backward가 y에 대한 x의 전체 그래디언트를 계산하도록 하기 위해, 어떤 벡터를 제공해야 한다.

y = x * x
y.backward(gradient=torch.ones(len(y)))  # Faster: y.sum().backward()
x.grad

특정 계산을 최종결과에서 제외하는 방법이 있다.

예를들어, 어떤 중간 계산 결과에 대한 그래디언트를 계산하고 싶지 않을 때, z = x y와 y = x x에 대해서 x에 대한 z의 직접적인 영향에만 집중하고 싶은 경우, y와 동일한 값을 가지지만 생성 방식이 제거된 새로운 변수 u를 만든다. u는 그래프에서 ancestors을 갖지 않게된다.

x.grad.zero_()
y = x * x
u = y.detach()
z = u * x

z.sum().backward()
x.grad == u # z = x * u 에서 u만 남음 

control flow (e.g., conditionals, loops, and arbitrary function calls)에 관계없이 여전히 gradient를 구할 수 있다.

def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c
    
a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()

a.grad == d / a # tensor(True)

2.6 Probability and Statistics

Machine learning의 모든 것은 불확실성(uncertainty)이다.

지도학습: 알려진 특징(Features)을 바탕으로 알려지지 않은 대상(Target)을 예측
비지도학습: 특정 측정값을 관찰할 확률을 아는 것은 그 측정값들이 이상한지 판단하는 데 도움
강화학습: 다양한 환경에서 지능적으로 행동하는 에이전트를 개발하는 데 필요

확률(Probability)은 불확실성 하에서 추론하는 것과 관련된 수학 분야

동전 던지기 예제

%matplotlib inline
import random
import torch
from torch.distributions.multinomial import Multinomial
from d2l import torch as d2l

num_tosses = 100
heads = sum([random.random() > 0.5 for _ in range(num_tosses)])
tails = num_tosses - heads
print("heads, tails: ", [heads, tails])

# Multinomial 활용하면 
fair_probs = torch.tensor([0.5, 0.5])
Multinomial(100, fair_probs).sample()

일반적으로 표본이 증가할수록 이론에 수렴하게 되고 이를 큰 수의 법칙(law of large numbers)라 부른다. 또한, 중심극한정리(central limit theorem)에 따르면 많은 상황에서 표본 크기가 커질수록 이러한 오차는 감소한다.

counts = Multinomial(1, fair_probs).sample((10000,))
cum_counts = counts.cumsum(dim=0)
estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)
estimates = estimates.numpy()

d2l.set_figsize((4.5, 3.5))
d2l.plt.plot(estimates[:, 0], label=("P(coin=heads)"))
d2l.plt.plot(estimates[:, 1], label=("P(coin=tails)"))
d2l.plt.axhline(y=0.5, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Samples')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend();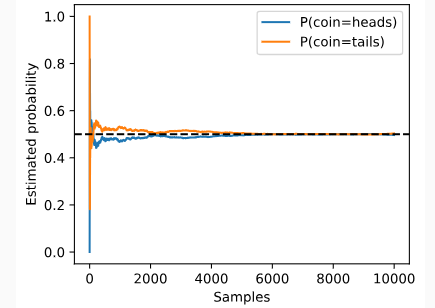

랜덤성을 대할 때는 sample/outcome space 집합 S를 정의한다. 예로 S = {heads, tails}
Events는 sample space의 부분집합이다. $z \in A$을 만족 해야한다.

확률 함수는 실수 값에 매핑 되어야 한다. $P: A \subseteq -> [0,1]$ 확률은 $P(A)$로 정의된다. 또한, 아래 특징들을 만족한다.

• $A$는 음수가 아닌 실수 값이다. $P(A)>=0$
• 전체 sample space에 대한 확률은 1이다. $P(S)=1$
• 어떤 셀 수 있고 연속적인 events에 대해서 mutually exclusive ($A_i \cap A_j = 0)$ 하고 이 중 하나라도 발생할 확률은 개별 확률의 합과 같다. $P(U_{i=1}^{\infin} A_i) = \Sigma_{i=1}^{\infin} P(A_i)$

확률에서 중요한 건 Random variable이다. 이는 기본 표본 공간(sample space)에서 값의 집합으로 매핑하는 것이다. 더불어, 이산적(Discrete) 또는 연속적(Continuous)일 수 있다. 이산 랜덤 변수는 셀 수 있는 결과를 갖는 반면, 연속 랜덤 변수는 셀 수 없는 결과를 갖는다. 연속 랜덤 변수의 경우, 특정 값이 발생할 확률은 0이지만, 해당 값의 밀도는 0이 아닐 수 있다. 연속 랜덤 변수에 대한 확률은 밀도 함수에 대한 구간의 적분을 통해 계산된다. 예를 들어, 특정 높이를 정확히 측정하는 것보다는 그 높이가 특정 구간 안에 있는지 여부가 더 중요할 수 있다.

Random variable이 취하는 값은 표본 공간의 부분 집합에 해당하며, 부분적으로 겹치거나 완전히 분리될 수 있기 때문에 한 무작위 변수가 취하는 값을 알면 다른 무작위 변수의 값에 대한 믿음을 업데이트할 수 있다.

Multiple random variables에서 두 변수가 취할 수 있는 조합에 확률을 할당하는 확률 함수를 Joint probability 라고 부른다. 이를 P(A=a,B=b)로 표현하며 ,는 and로 생각하면 된다.

$P(A=a) = \Sigma_v P(A=a, B=v)$
조건부 확률 (Conditional Probability) $P(B=b | A=a) = \frac{P(A=a,B=b)}{P(A=a)}$

이로부터 Bayes'theorem을 유도할 수 있다.

$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$
만약, 우리가 P(B|A), P(A) 그리고 P(B)를 예측할 수 있다면 P(A|B)를 예측할 수 있게된다. 그러나, 종종 P(B)를 직접적으로 접근할 수 없는 경우들이 있다. 이 경우에는 단순화 시킨다.
$P(A|B) \propto P(B|A)P(A)$ 또한, P(A|B)가 1로 normalized 되어야 함을 알기 때문에
$P(A|B)= \frac{P(B|A)P(A)}{\Sigma_a P(B|A=a)P(A=a)}$

Bayesian statistics에서는 사전 믿음(Prior) P(H)와 우도(likelihood, 수집된 증거의 값을 관찰할 가능성을 나타내는 확률 함수) P(E|H)를 사용하여 사후 확률(Posterior) P(H|E)를 업데이트 한다.

또한 Marginalize라는 개념을 통해 Joint distribution에서 variable을 drop할 수 있다.
$\Sigma_a P(A=a|B) = 1$ 이므로 $\Sigma_a P(B|A=a)P(A=a) = \Sigma_a P(B,A=a) = P(B)$

다음으로 아래를 만족하면 independent, 독립이라고 한다.
$P(A|B)=P(A)$ 결과적으로, $P(A,B)=P(A|B)P(B)=P(A)P(B)$

독립성은 어떤 기본 분포에서 데이터를 연속적으로 추출할 때(강한 통계적 결론을 내릴 수 있을 때) 또는 데이터의 다양한 변수 간에 독립성이 유지되어 이 독립성 구조를 인코딩하는 더 간단한 모델로 작업할 수 있을 때 특히 유용하다.

흥미로운 점은 두 변수는 일반적으로 독립적일 수 있지만 세 번째 변수를 조건부로 지정하면 종속 변수가 될 수도 있다. 이는 종종 두 개의 무작위 변수가 세 번째 변수의 원인에 해당하는 경우에 발생한다. 서로 관련이 없는 두 사건이 공통의 원인을 가지고 있을 때는 반대로 독립 변수가 될 수 있다.

일반적으로, random varialbe X에 대한 expectation(평균)은
$E[x] = E_{x \sim P[x]} = \Sigma_x xP(X=x)$

확률 밀도 함수는
$E[x]=\int x dp(x)$, $E_{x \sim P[f(x)]} = \Sigma_x f(x)P(x), \int f(x)p(x) dx$

유사하게 분산은
$Var[X]=E[(X-E[X])^2]=E[X^2]-E[X]^2$
$Var_{x \sim P[f(x)]}=E_{x \sim P[f^2(x)]}-E_{x \sim P[f(x)]^2}$

공분산 행렬은 $u := E_{x \sim P[x]} 일 때


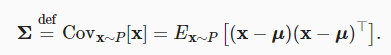
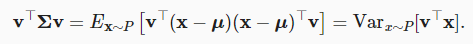
모든 선형 함수에 대한 분산을 계산할 수 있다. 대각선을 벗어난 요소는 좌표가 얼마나 상관관계가 있는지 알려주며, 값이 0이면 상관관계가 없음을 의미하고, 양수 값이 클수록 상관관계가 강하다는 것을 의미한다.