이진 트리 Binary Tree
이진 트리는 기존 선형 배열에서의 삽입/삭제를 보다 더 효율적으로 하기 위해 탄생하였다.
이는 Linked List 자료구조를 사용하여 삽입과 삭제가 선형 구조보다 훨씬 효율적이다.
| 자료구조 | 탐색 | 삽입 | 삭제 |
|---|---|---|---|
| 선형 배열 | O(n) | O(n) | O(n) |
| 이진 트리(Linked List 구조) | O(n) | O(1) | O(1) |
이진 트리는 어떤 컨셉인지 알아보자.
노드가 왼쪽 자식과 오른쪽 자식만을 갖는 트리를 이진 트리라고 한다.
이때, 두 자식 가운데 하나 또는 둘 다 존재하지 않는 노드가 있어도 상관없다.
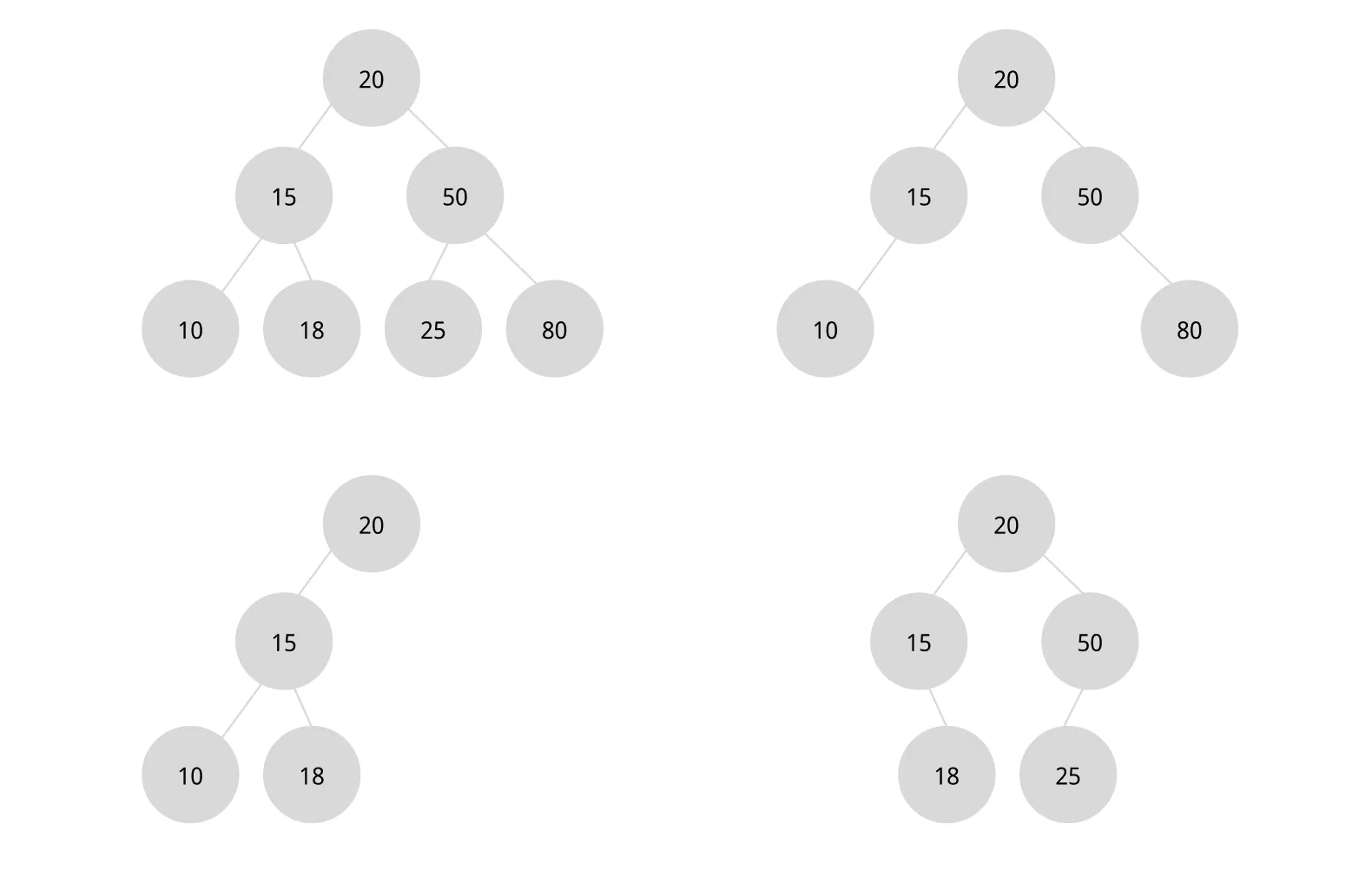
위 4개의 트리는 모두 이진 트리로 볼 수 있다.
또, 이진 트리의 특징은 왼쪽 자식과 오른쪽 자식을 구분한다는 점이다.
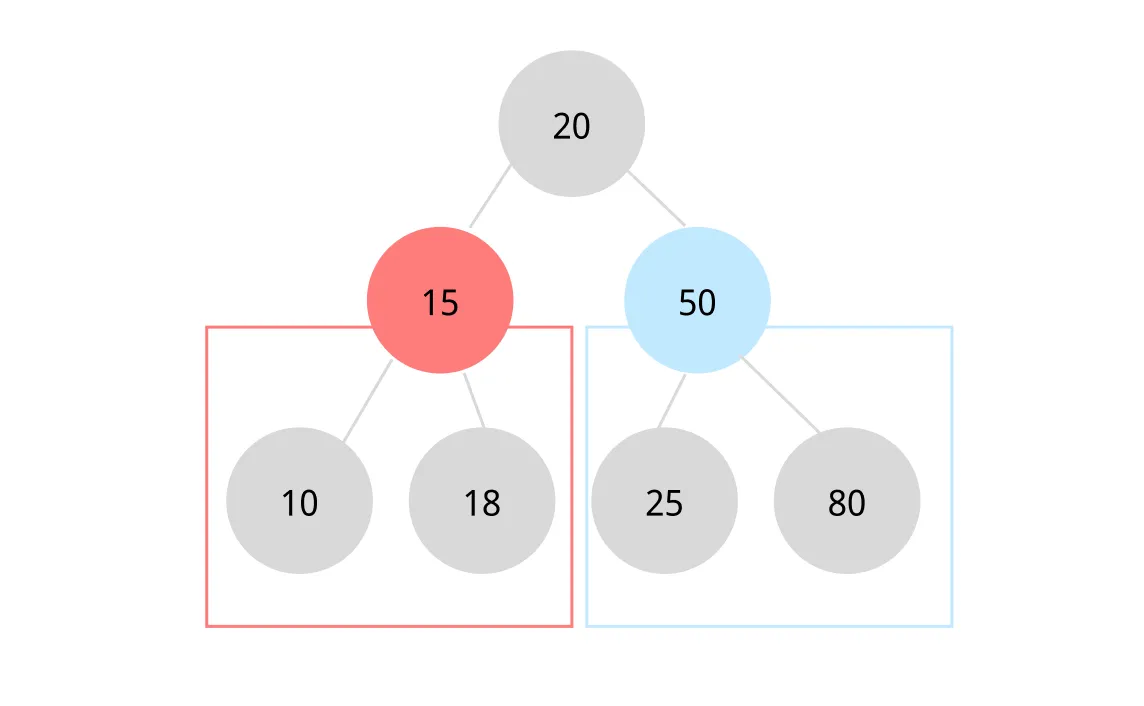
15 노드의 왼쪽 자식은 10, 오른쪽 자식은 18이다.
왼쪽 자식을 루트로 하는 서브트리를 왼쪽 서브트리 left subtree라고 하고,
오른쪽 자식을 루트로 하는 서브트리를 오른쪽 서브트리 right subtree라고 한다.
20의 왼쪽 서브트리는 15를 루트로 하는 빨간 부분, 20의 오른쪽 서브트리는 50을 루트로 하는 파란색 부분이다.
하지만 의문이 든다. 이진 트리는 자식을 하나만 가져도, 혹은 가지지 않아도 된다. 그러면 트리의 노드가 깊어지고 최악의 경우 한 방향으로 쭉 나열된다면 선형 구조와 동일해지지 않나?
균형 검색 트리 self-balancing search tree
이런 약점을 개선하기 위해 높이를 O(log n)으로 제한하여 고안된 검색 트리가 균형 검색 트리 self-balancing search tree라고 한다.
다음에 더 자세히 다뤄보자.
[ 이진 구조를 가진 균형 검색트리 ]
- AVL tree
- red-black tree
[ 이진이 아닌 균형 검색 트리 ]
- B-tree
- 2-3 tree
이진 검색 트리 Binary Search Tree
이진 검색 트리(BST)는 이진 트리의 특수한 형태를 가진 자료구조로, 더 빠른 검색/삽입/삭제를 가능하게 하기 위해 정렬 조건을 추가한 구조이다.
또한, 이진 탐색 트리는 이진탐색 알고리즘의 개념을 연결리스트 방식으로 구현한 자료구조라고 볼 수 있다. 선형 탐색에 비해 수많은 데이터를 효율적으로 탐색할 수 있으면서도, 삽입과 삭제 연산을 보다 더 효율적으로 할 수 있다.
| 자료구조 | 검색 | 삽입 | 삭제 |
|---|---|---|---|
| 선형 배열 | O(n) | O(n) | O(n) |
| 이진 트리(Linked List 구조) | O(n) | O(1) | O(1) |
| 이진 탐색 트리 | O(log n) | O(log n) | O(log n) |
이진 검색 트리의 특징은 모든 노드가 아래 두 조건을 만족해야 한다는 것이다.
- 왼쪽 서브트리 노드의 값보다 자신의 노드 값 보다 작아야 한다.
- 오른쪽 서브트리 노드의 값보다 자신의 노드 값 보다 커야 한다.
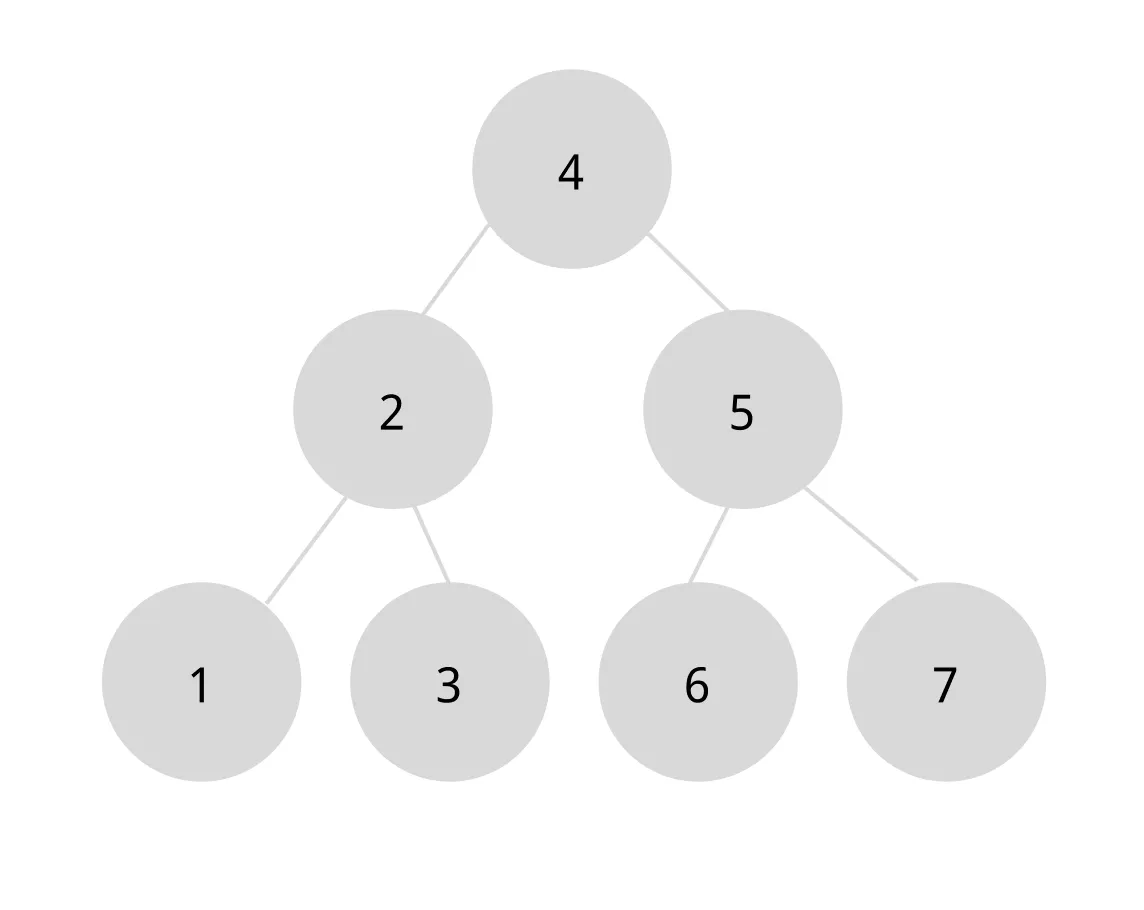
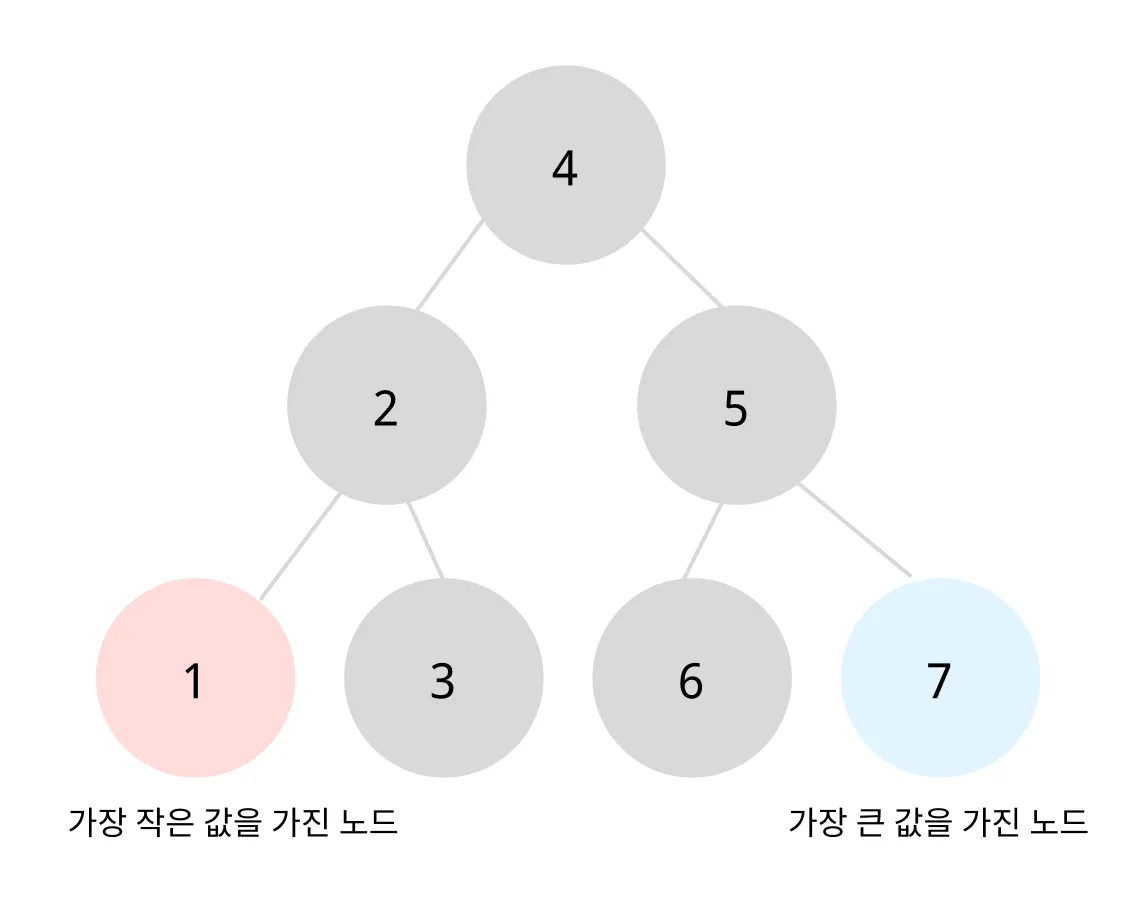
BST를 순회할 때는 inorder 방식을 쓴다. 왼쪽 서브트리-루트-오른쪽 서브트리 순서로 순회한다.
위의 트리를 중위순회(왼쪽-루트-오른쪽) 해보면
1→2→3→4→5→6→7
다음과 같이 노드값을 오름차순으로 얻을 수 있다.
이진 검색 트리는 아래에서 삽입과 삭제가 이루어진다.
그리고 구조의 특징 때문에 가장 왼쪽 leaf 노드의 값이 최소값이며, 가장 오른쪽 leaf 노드의 값이 최대값이다.
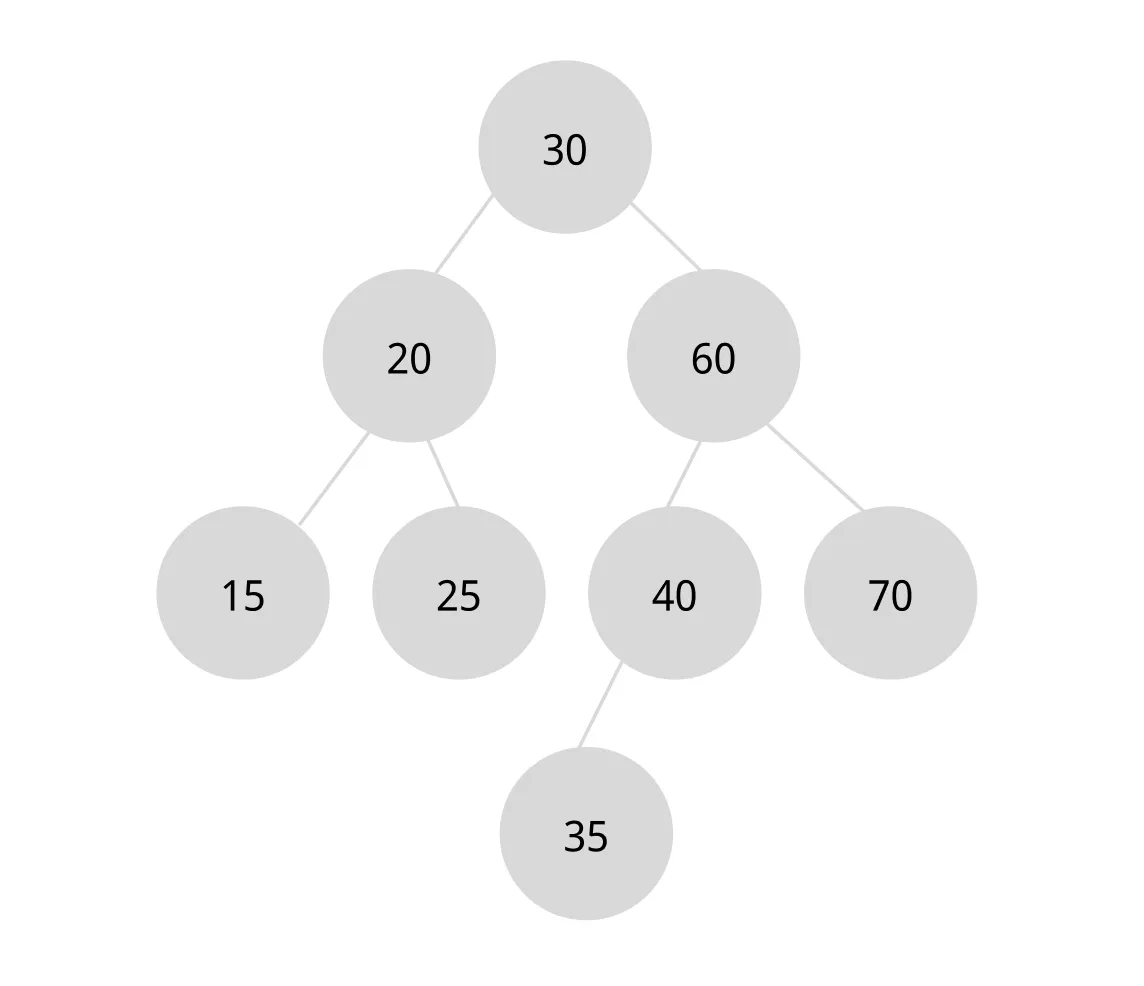
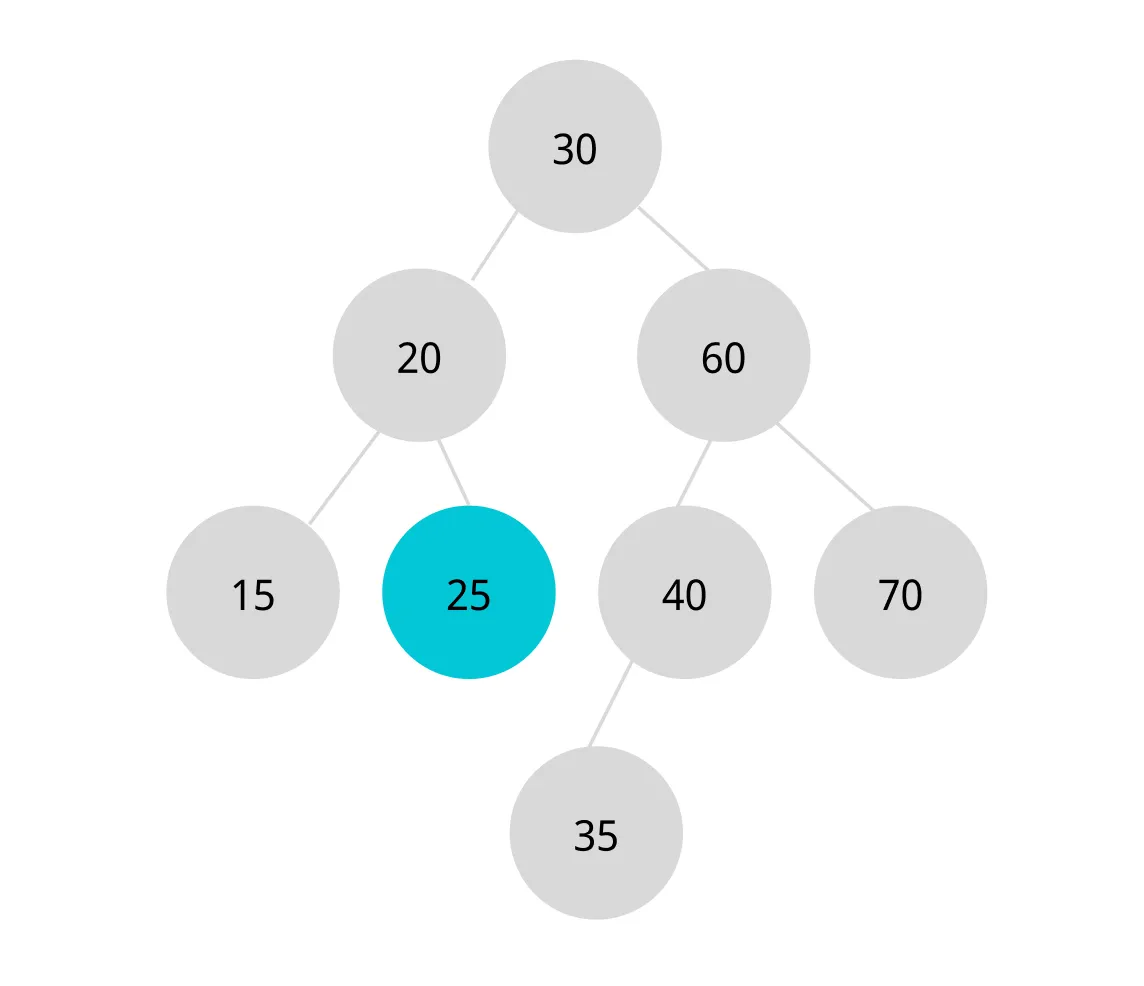
검색 search 과정
값이 25인 노드를 찾아보자.
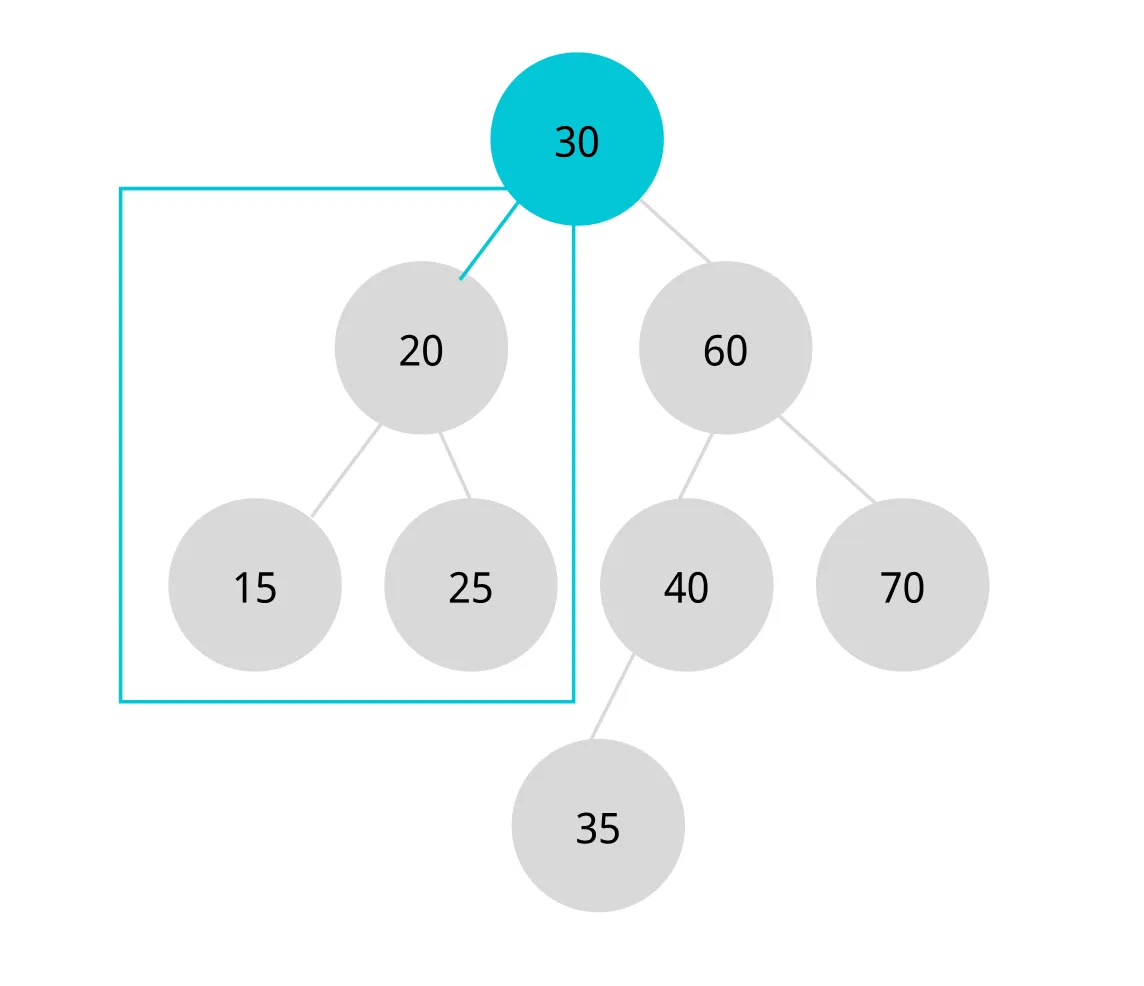
- 루트의 값(30) 보다 작으므로 왼쪽 서브트리로 이동한다.
- 루트(20) 보다 크기 때문에 오른쪽 서브트리로 이동한다.
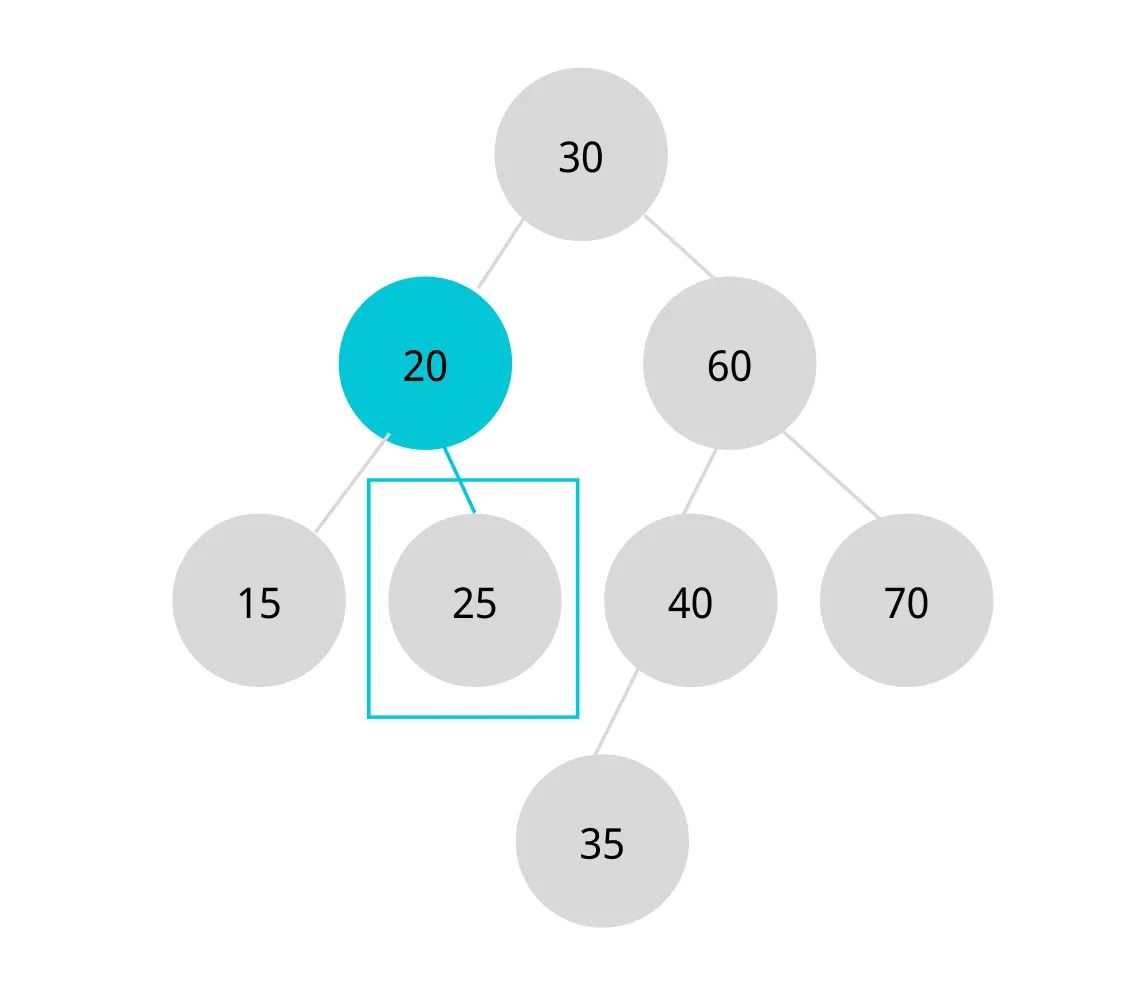
- 이동한 오른쪽 서브트리의 루트(25)와 같다. 탐색 성공!
삽입 add 과정
노드를 삽입할 때는 삽입한 뒤에도 이진 검색 트리의 조건을 유지해야 한다는 점을 유의해야 한다.
따라서 삽입하고자 하는 노드가 어디에 위치해야 할 지 검색한 후, 해당 위치에 삽입하면 된다.
조건을 유지하며 50을 삽입해보자.
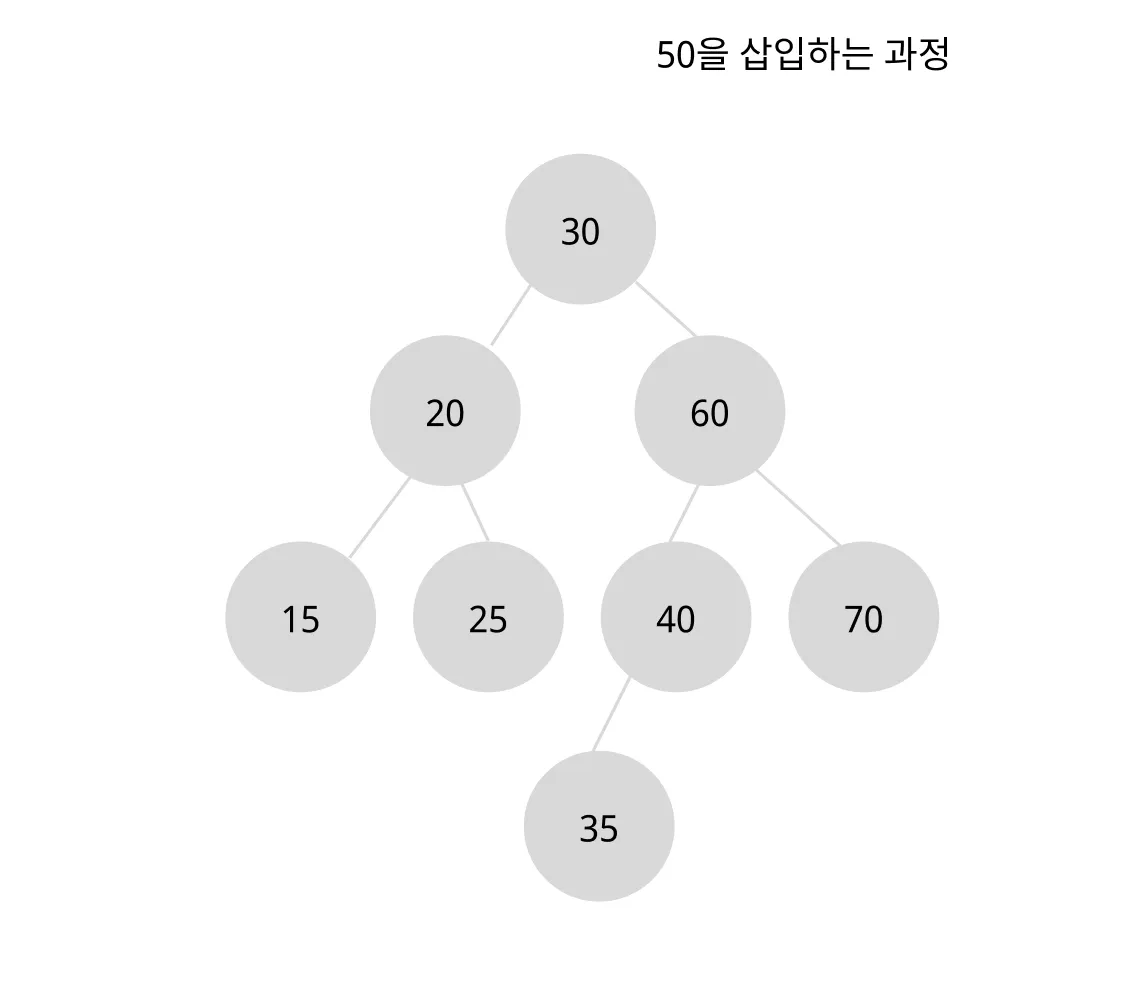
- 새로운 노드의 값 50이 추가될 위치를 검색한다.
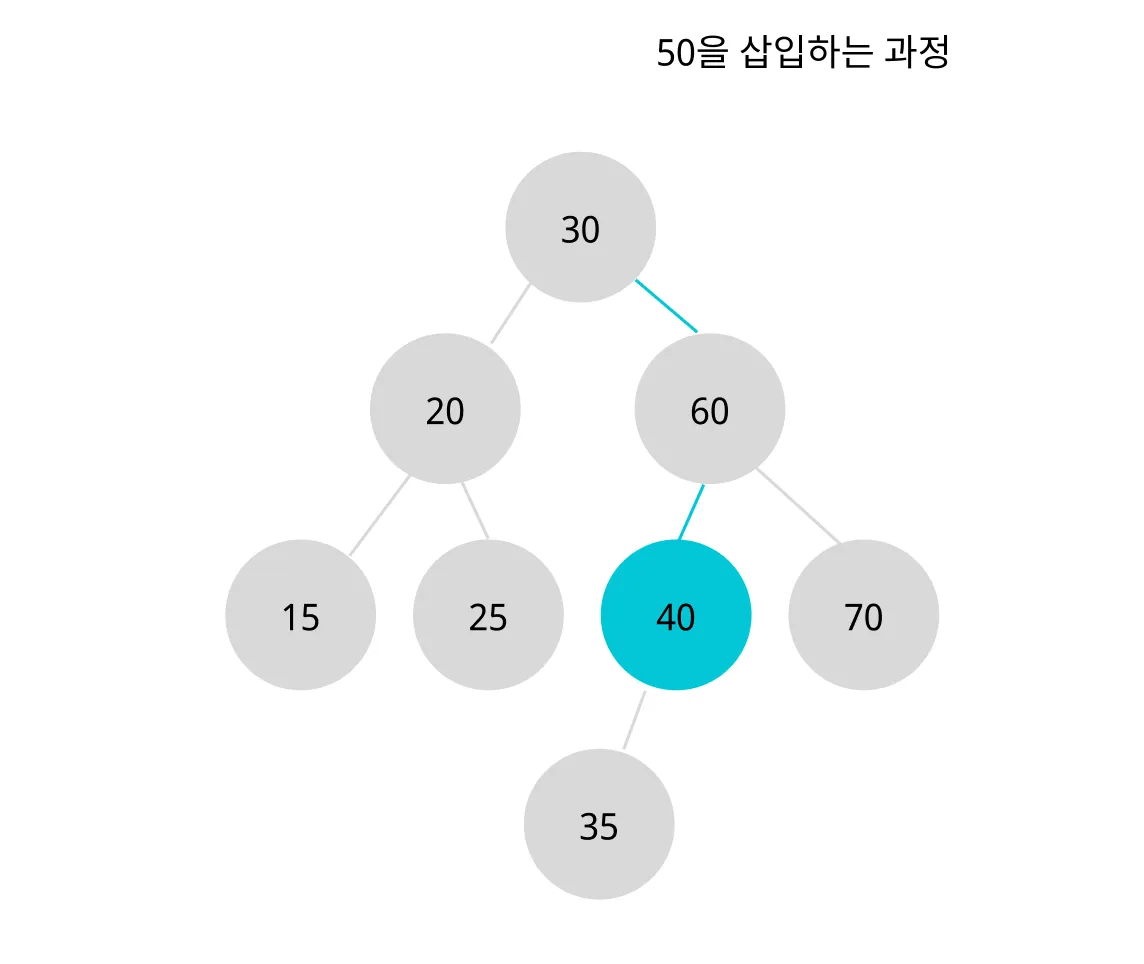
- 루트(40) 보다 크기 때문에 40의 오른쪽 노드로 삽입한다.
삭제 remove 과정
삭제는 다소 복잡하게 느껴질 수 있다. 세 가지 경우로 나뉘기 때문이다.
1. 자식 노드가 없는 노드를 삭제하는 경우
2. 자식 노드가 하나인 노드를 삭제하는 경우
3. 자식 노드가 두개인 노드를 삭제하는 경우
이렇게 나누어 삭제 과정을 따라가보자.
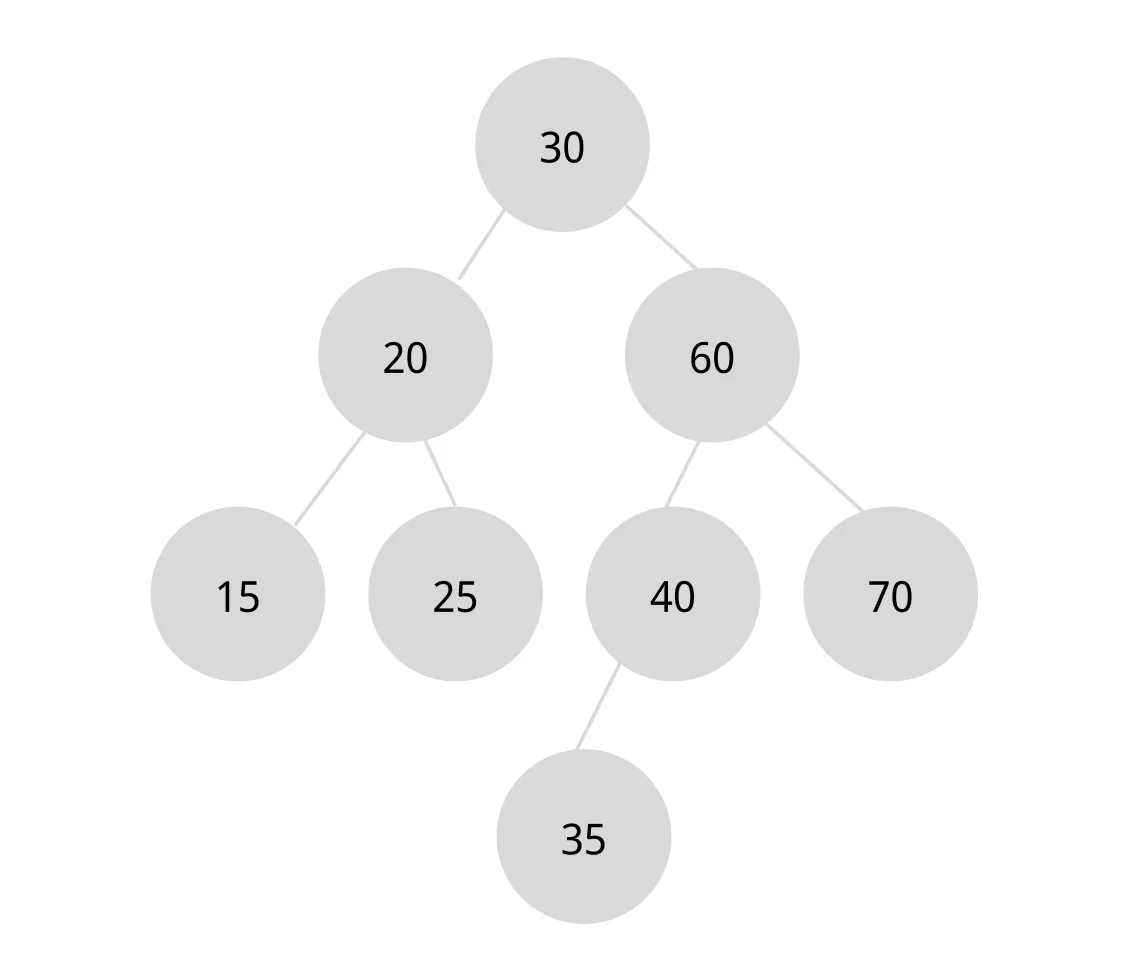
자식 노드가 없는 노드를 삭제하는 경우
자식 노드가 없는 leaf 노드, 35를 삭제헤보자.
35를 삭제하는 경우, 우선 35를 값으로 하는 노드가 어디에 있는지 검색한다.
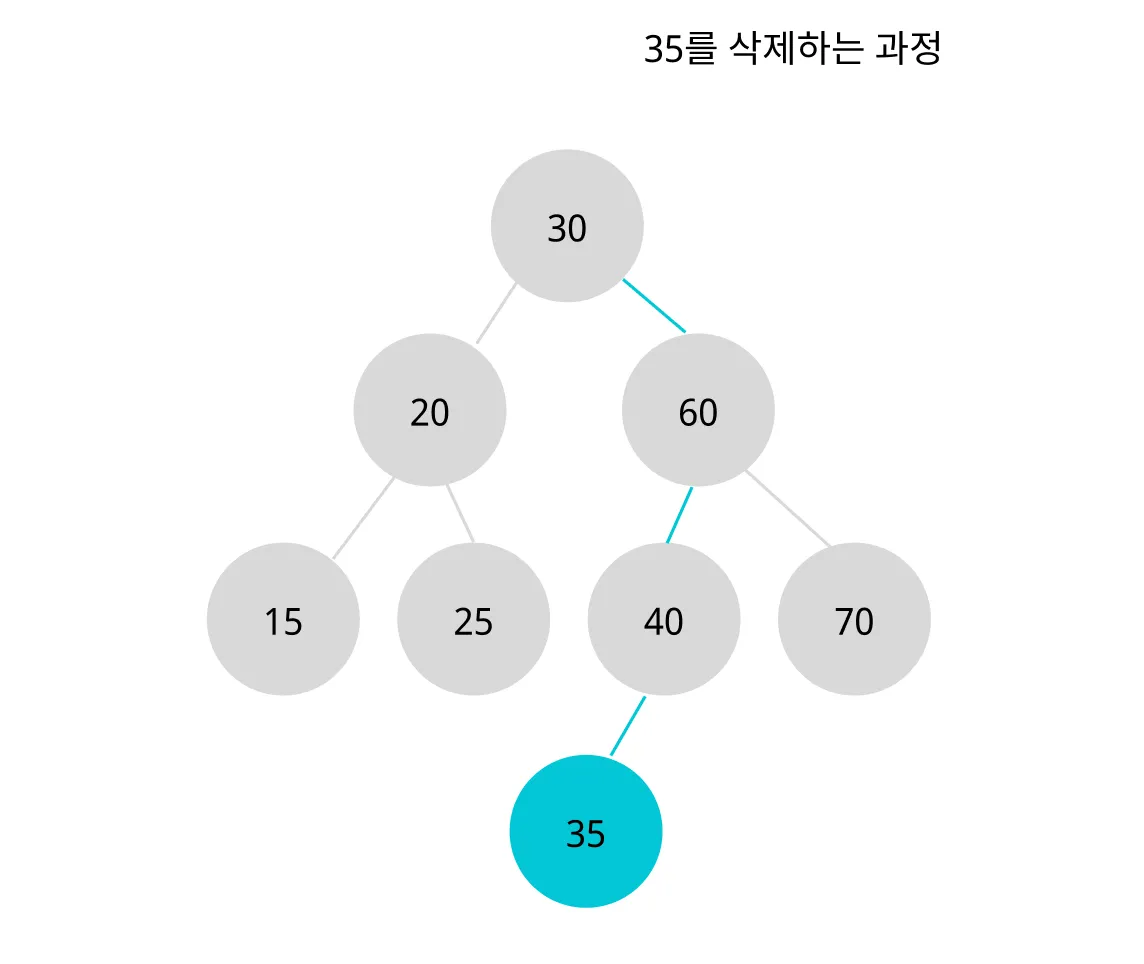
35 노드를 가리키는 노드인 40이 35를 가리키지 않도록 연결을 끊어준다.
즉, 40의 왼쪽 포인터를 NULL로 바꿔준다.
자식 노드가 1개인 노드를 삭제하는 경우
40을 값으로 하는 노드를 삭제해보자.
동일하게 노드가 어디에 위치해 있는 지 먼저 검색한다.
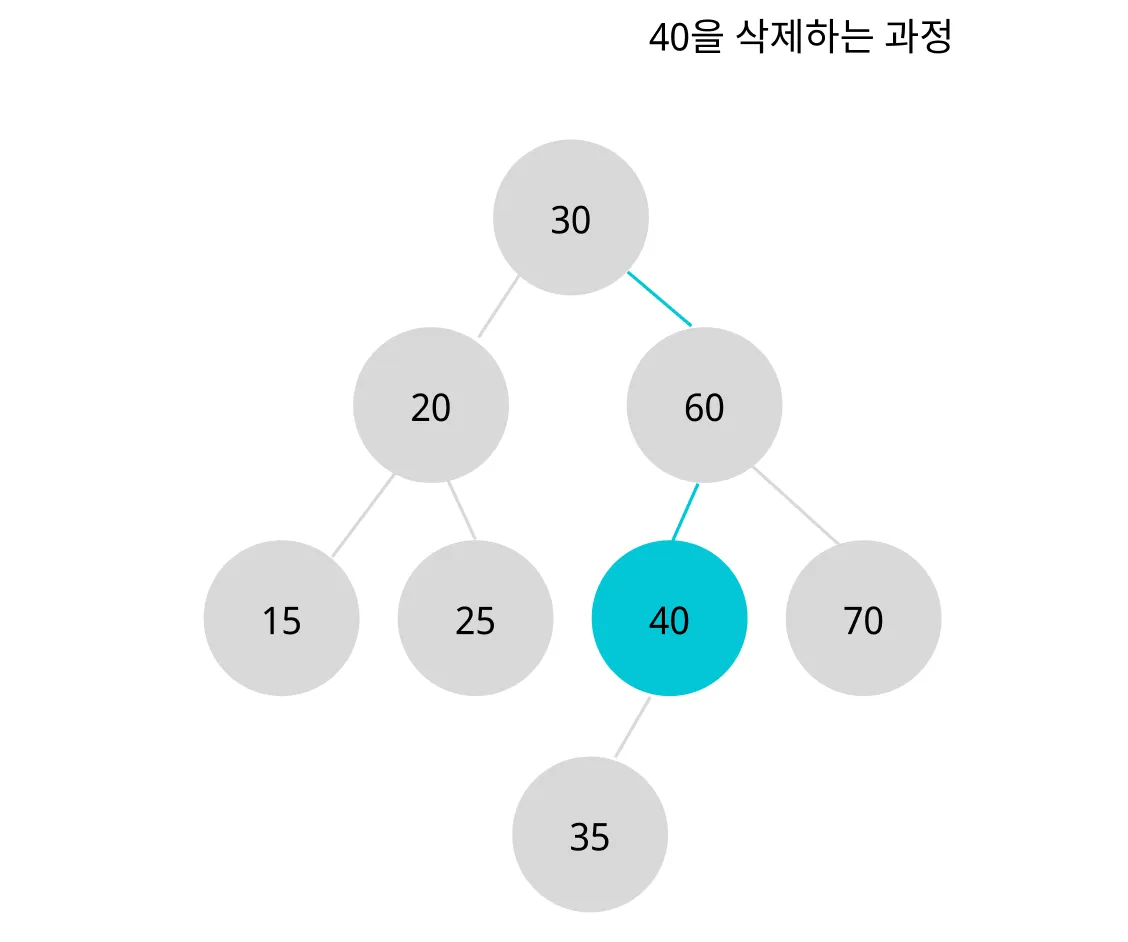
40을 가리키는 노드인 60의 왼쪽 포인터를 40의 왼쪽 자식 노드인 35로 바꿔준다.
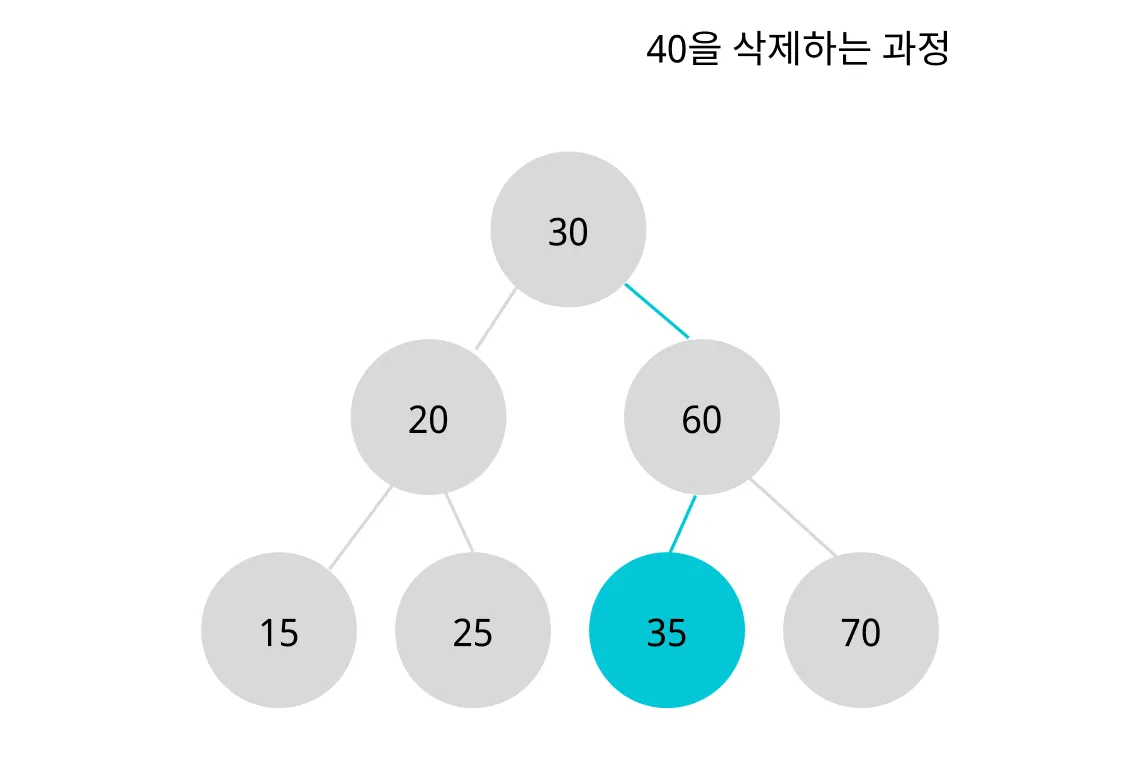
자식 노드가 2개인 노드를 삭제하는 경우
검색, 삽입에 비해 다소 복잡하므로 그 과정을 먼저 살펴보자.
우선, 삭제할 노드의 왼쪽 서브트리에서 키값이 가장 큰 노드를 검색한다.
검색한 노드를 삭제 위치로 옮긴다. 즉, 검색한 노드의 데이터를 삭제할 노드 위치에 복사한다.
옮긴 노드를 삭제한다.
이 마지막 과정에서 옮기는 노드의 자식이 있는 경우, 없는 경우로 나뉜다.
옮기는 노드의 자식이 없는 경우부터 그림으로 이해해보자.
(1) 옮기는 노드의 자식이 없는 경우
삭제할 노드를 찾아간다.
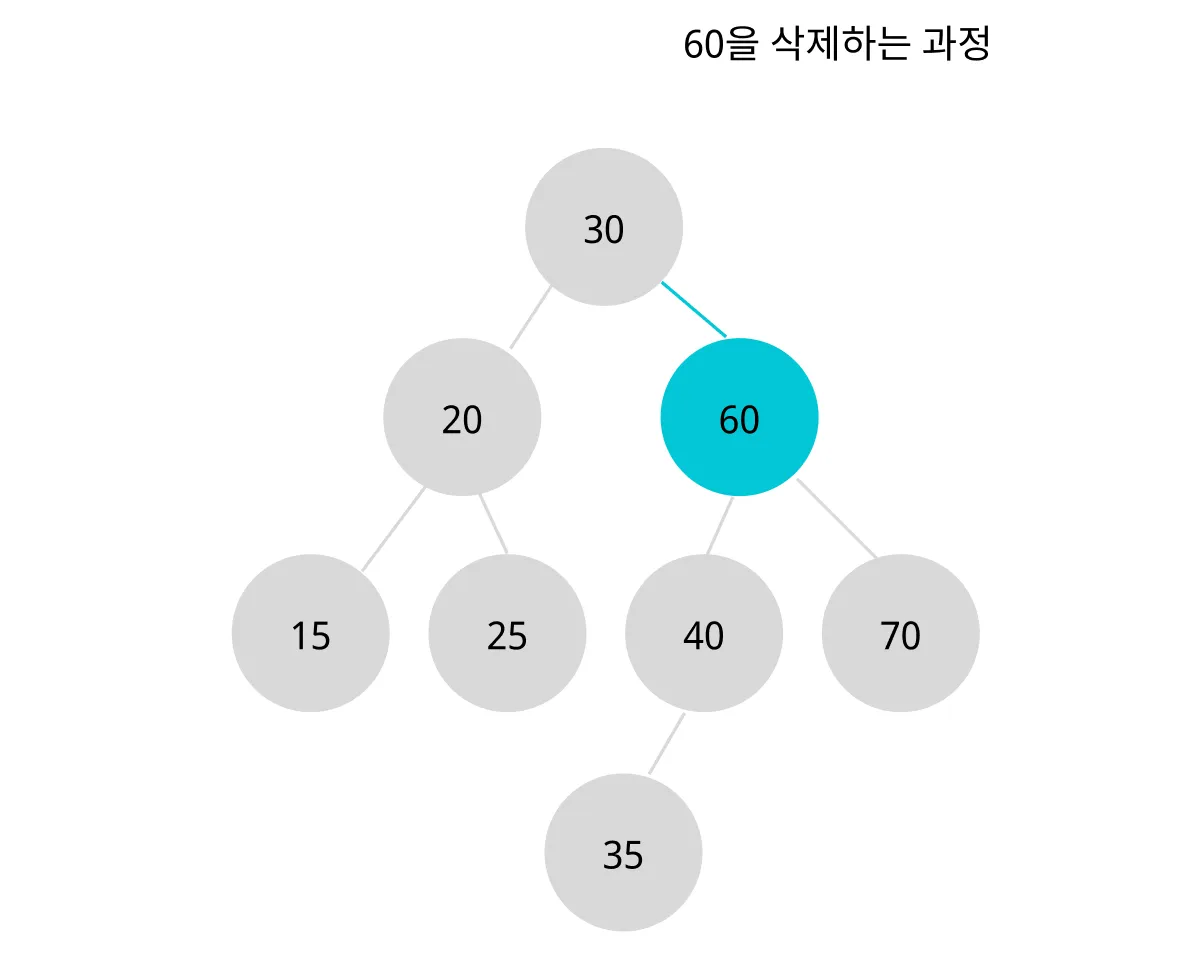
삭제할 노드의 왼쪽 서브트리에 집중한다.
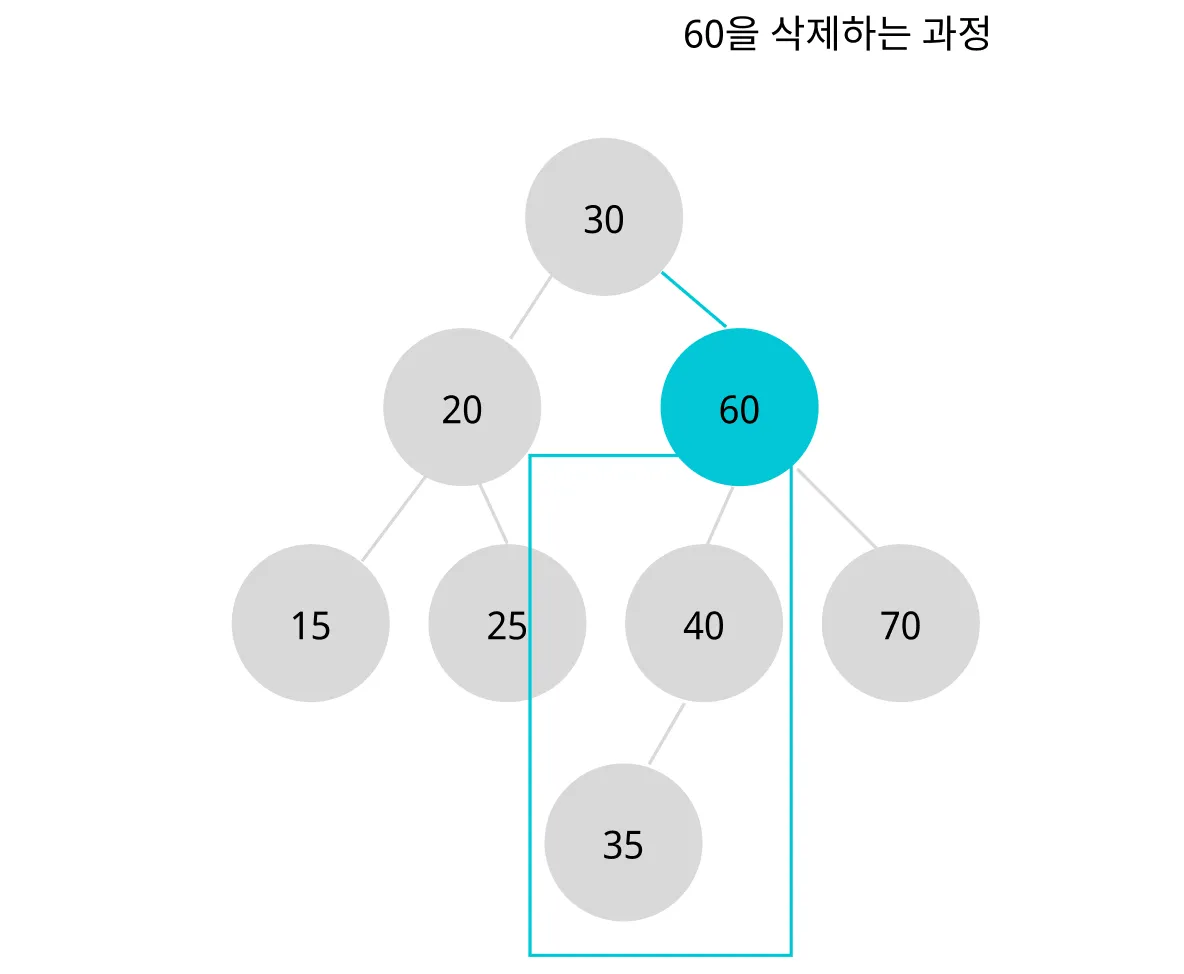
이 중 가장 큰 값을 선택하여 삭제하고자 하는 노드에 복사한다.
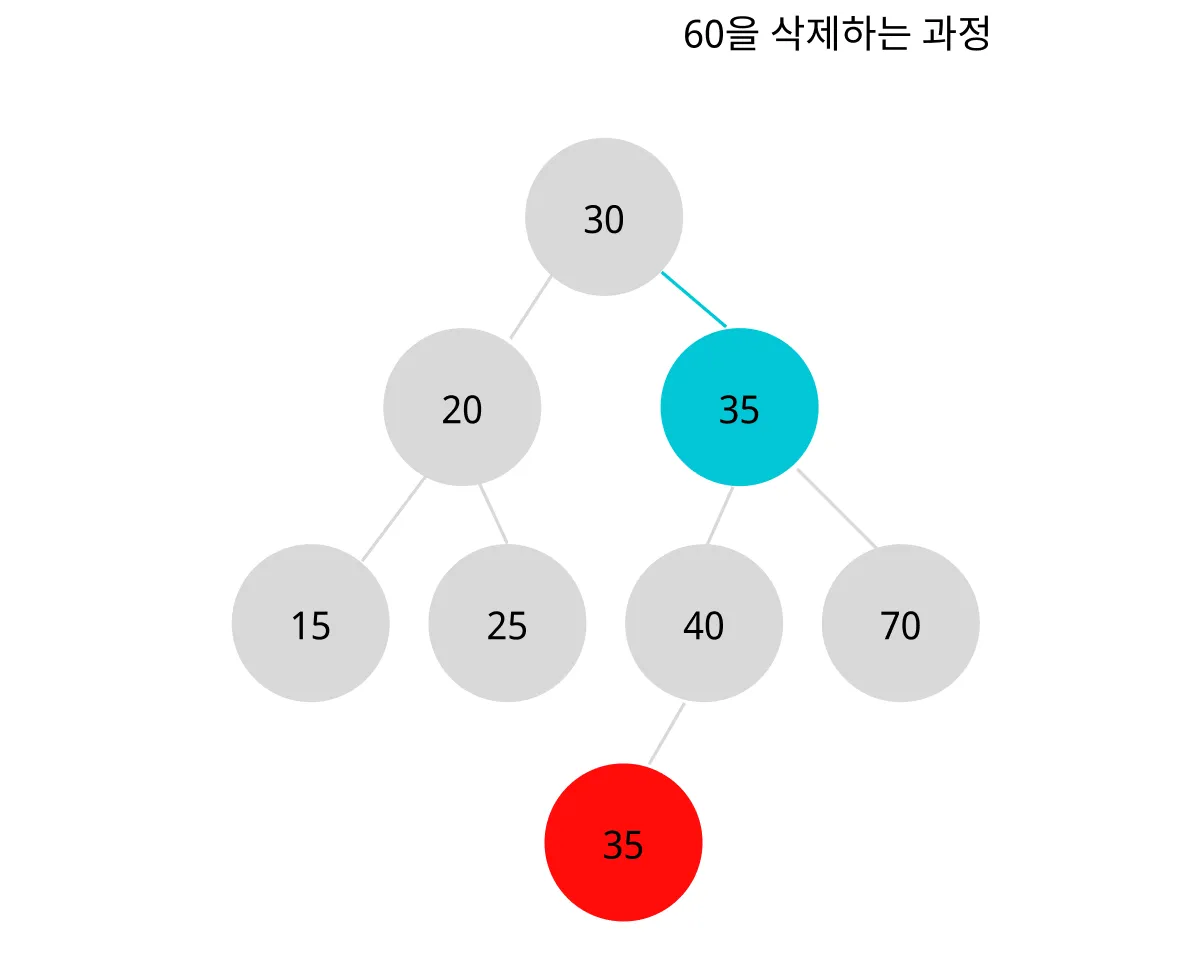
옮긴 노드의 자식이 없으므로 바로 삭제한다.(연결 포인터를 NULL로)
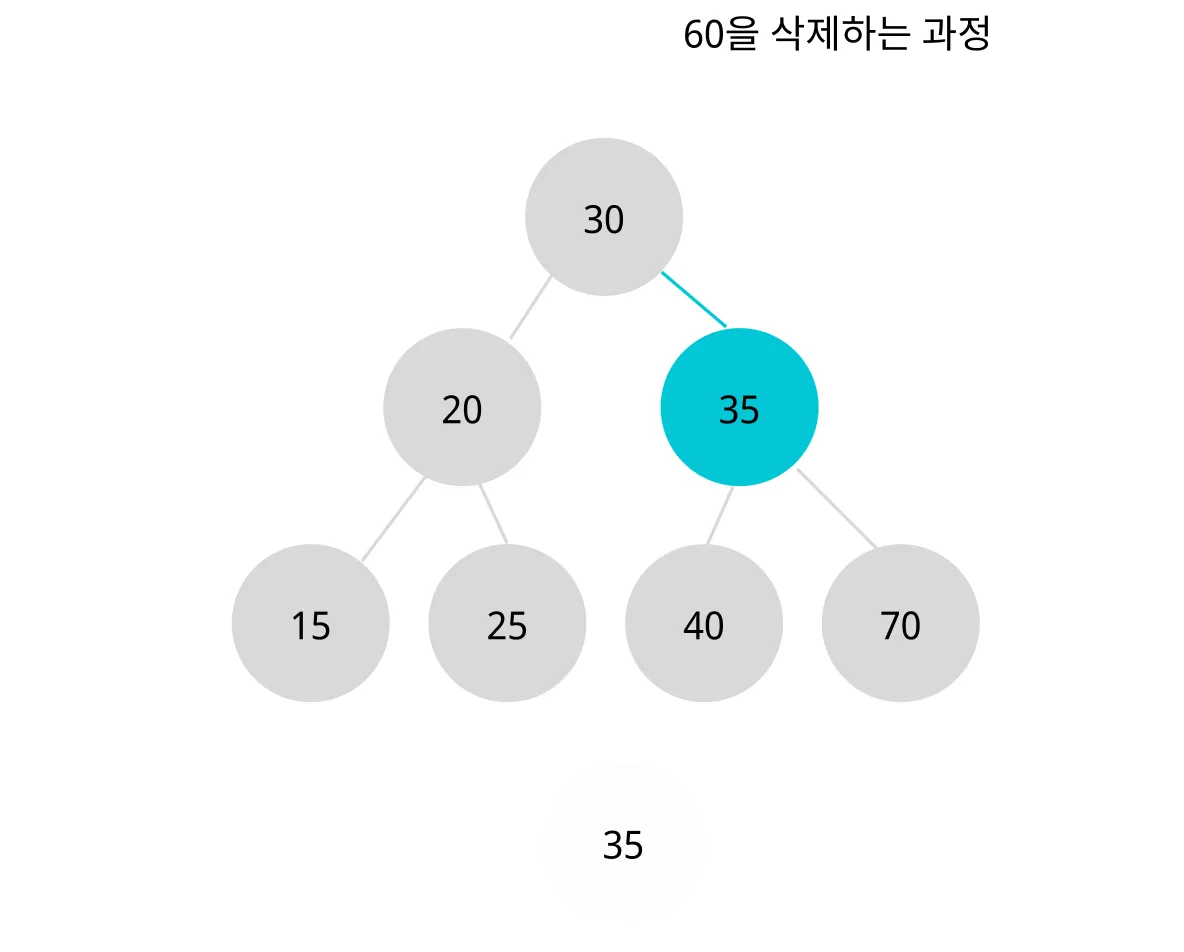
(2) 옮기는 노드의 자식이 있는 경우
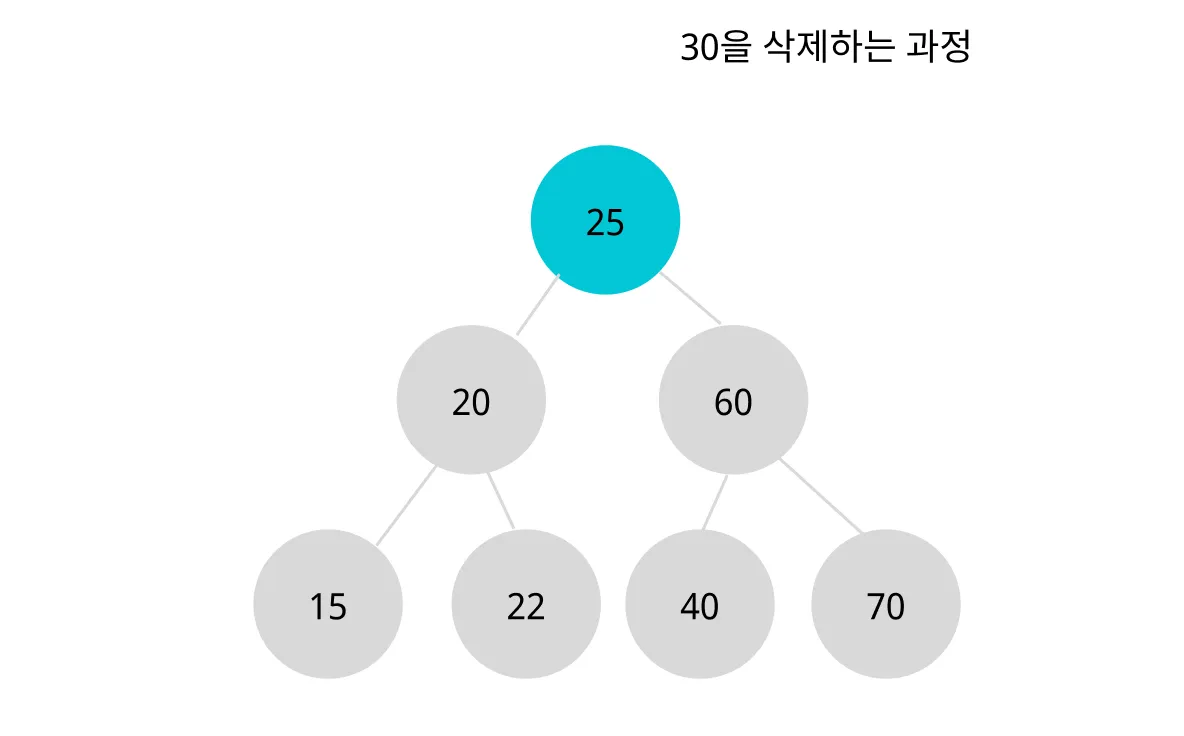
옮기는 노드의 자식이 있는 경우도 동일하게 삭제할 노드를 먼저 찾는다.
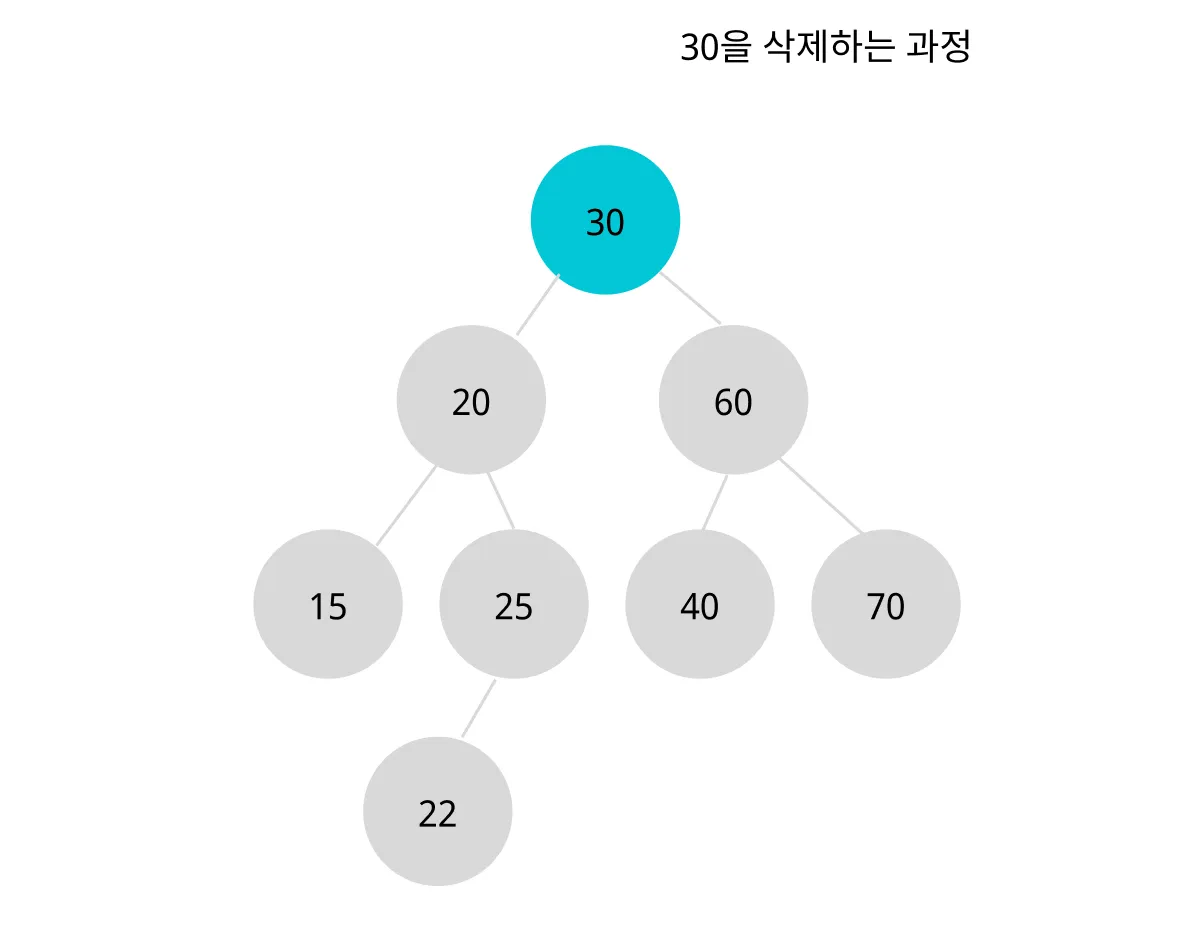
30을 삭제하기 위해서 왼쪽 서브트리에서 가장 큰 값을 찾는다.
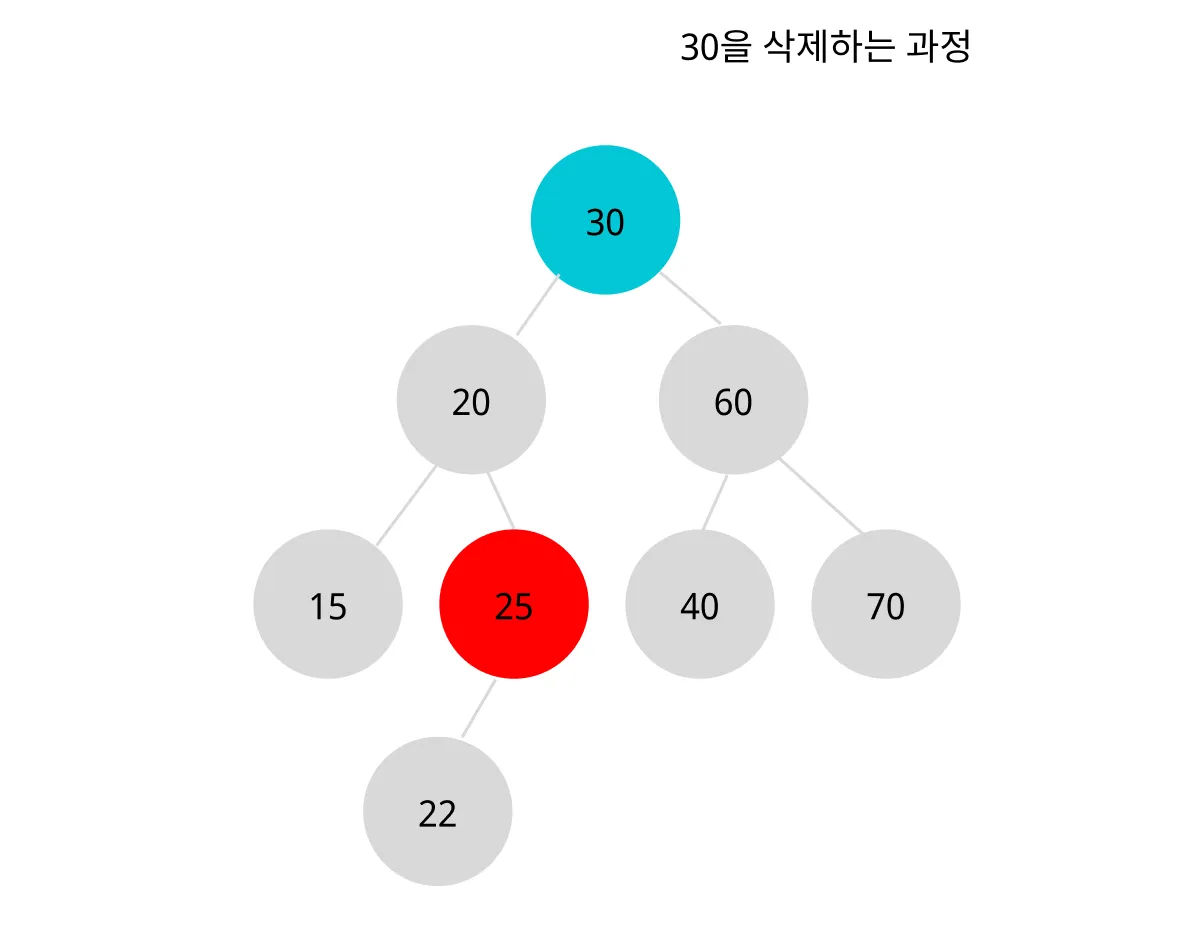
왼쪽 서브트리에서 가장 큰 값(25)을 삭제할 위치에 복사한다.
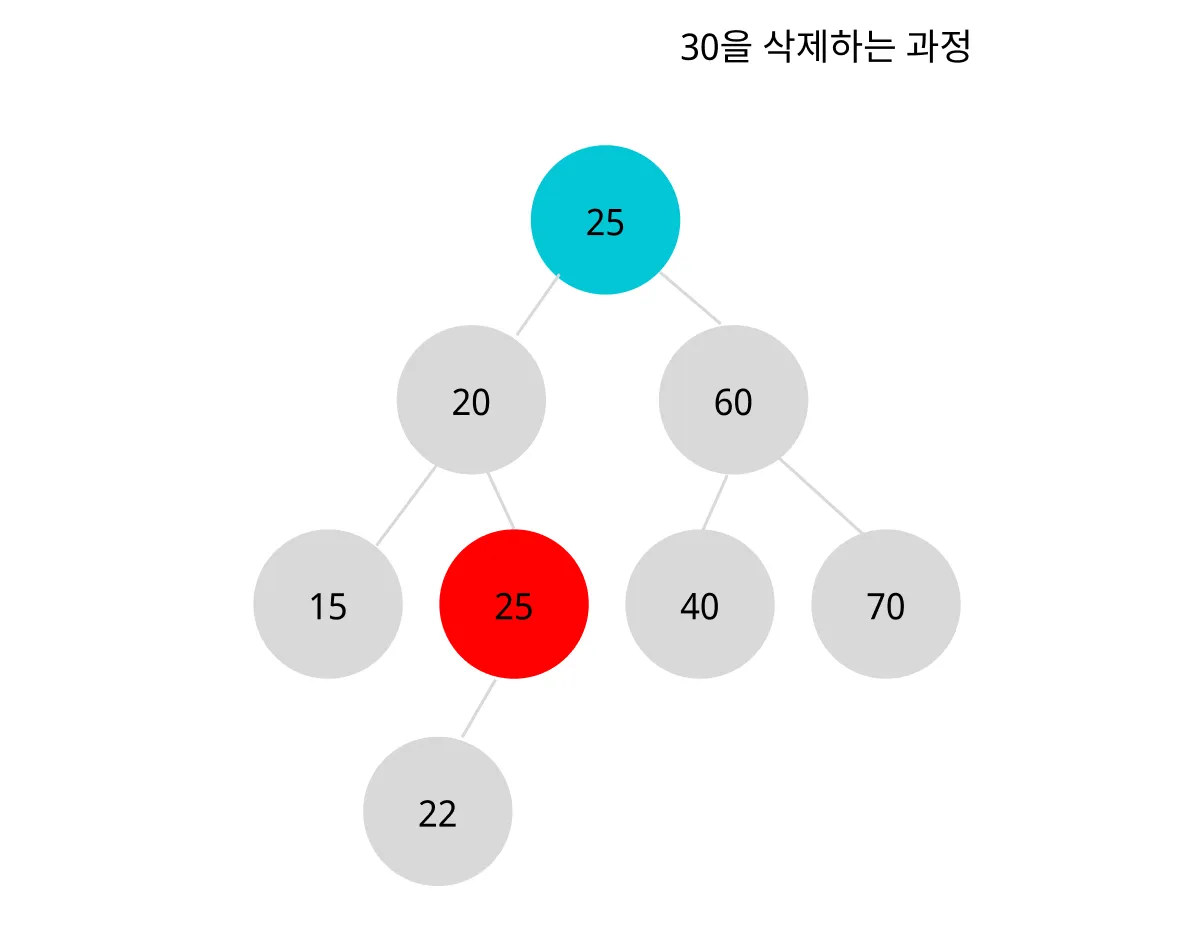
이제 옮긴 노드를 지워야 하는데 자식 노드(22)가 존재한다. 22의 위치를 찾아주어야 한다.
이 때는 ‘자식 노드가 1개인 경우 삭제하는 과정’에 따라 25 노드를 가리키는 20 노드의 오른쪽 포인터로 연결해준다.