문제
9020번 문제 바로보기
1700년 대 크리스티안 골드바흐라는 사람이 있었다고 한다. 골드바흐는 레온하르트 오일러에게 편지를 보냈는데 내용이 아래 이미지를 이론으로 설명한 내용이라고 한다.
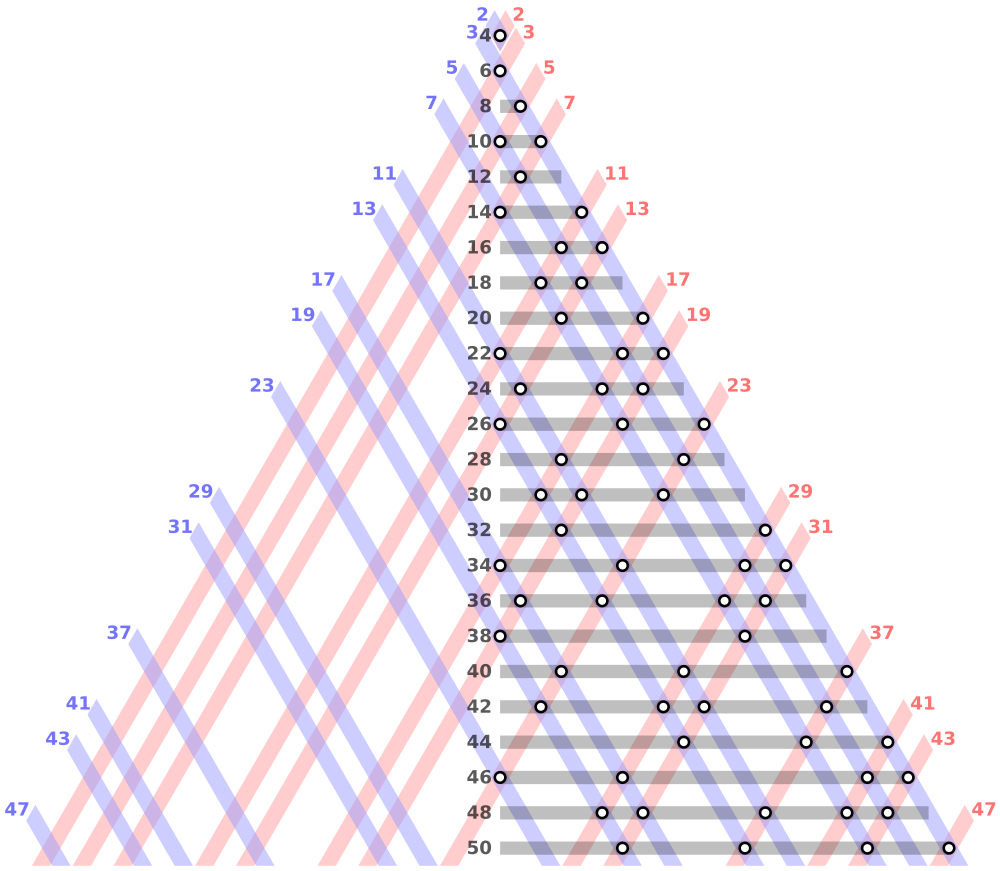
해당 내용을 추측하고 이론을 편지로 보내다니.. 나는 죽었다 깨어나도 수학자는 될 수 없을듯 하다.
골드바흐의 추측은 유명한 정수론의 미해결 문제로, 2보다 큰 모든 짝수는 두 소수의 합으로 나타낼 수 있다는 것이다. 또, 짝수를 두 소수의 합으로 나타내는 표현을 그 수의 골드바흐 파티션이라고 한다.
어찌되었든 2보다 큰 짝수 n이 주어졌을 때, 골드바흐 파티션을 출력하는 프로그램을 작성하라 했다.
고민
문제 마지막의 메세지가 나에게 풀이방식에 대한 힌트를 주었다.
"만약 가능한 n의 골드바흐 파티션이 여러 가지인 경우에는 두 소수의 차이가 가장 작은 것을 출력한다."
위 문구를 보고 아래와 같이 생각했다.
1. 차이가 가장 적으려면 출발점을 반절 값에서 시작해야겠다.
2. 반절값부터 한쪽은 1씩 줄어들고, 한쪽은 1씩 늘어나면서 그 값들이 소수가 맞는지 판별하기만 하면 되겠다.
아래와 같이 접근, 순서도를 짜봤다.

해결
from sys import stdin
T=int(stdin.readline()) #1. 테스트 케이스 개수를 받는다 = T
def prime(number): #2. 소수를 판별하는 함수를 만든다
if number<2:
return "No"
for j in range(2,int(number**0.5)+1):
if number%j==0:
return "No"
return "Yes"
for i in range(T):
n=int(stdin.readline()) #3. 값을 입력받아 n으로 지정하고,
a=int(n/2) #3. 반절 값을 시작으로 하나씩 줄여나갈 변수를 지정.
b=int(n/2) #3. 반절 값을 시작으로 하나씩 늘여나갈 변수를 지정.
for k in range(int(n/2)): #4. n 전체가 아닌 반절값만 증명하면 OK
if prime(a)=="Yes" and prime(b)=="Yes": #4-1. a,b 둘다 소수일 경우 Yes 출력
print(a,b)
break
else: #4-2. 아닐 경우 변수의 차이를 두어 확인
a=a-1
b=b+1리뷰
이전에 소수 문제를 풀다가 다른이 풀이에서 제곱근을 활용하여 소수를 찾아내는 방식을 보게되었다. 처음에는 이해가 안되었으나, 소수를 판별하는 아래 3단계를 보고 깨달았다.
1단계 : 판별하는 수 미만으로 소수인지 모두 확인하는 방법
예를들어 10이라면 2부터 9까지 10을 나눠보고 나머지가 0이 안나오면 소수로 정의하는 방식. 나는 이전에 1단계로 설계하여 풀었다.
2단계 : 1단계에서 한단계 발전하여 판별하는 수의 절반까지만 확인하는 방법
판별하는 수의 절반 이상의 숫자들은 나누었을 때 1과 2 사이의 자연수가 아닌 숫자가 나오므로 나머지가 0이 나올 수가 없다.
예를들어 100이라면 2~50까지만 확인하는 방법이다. 1단계보다 1/2를 줄일 수 있다.
3단계 : 소수를 판별하는 가장 효율적인 방법으로, 판별하는 수의 제곱근 만큼만 확인하는 방법
약수를 중심으로 구하는 원리인데, 예를들어 80의 약수는
1, 2, 4, 5, 8, 10, 16, 20, 40, 80이다.
(1x80 = 80, 2x40=80, 4x20=80...)
80의 제곱근은 8.xxx로, 위 약수의 중간 값에 해당한다. 이 원리로 약수 이전의 값까지만 확인하면 이후의 값을 확인 할 필요가 없게 된다.
이번 풀이에서 소수인지 판별하는 함수를 구할 때 for문의 '**0.5'가 3단계를 활용했기에 나오게 되었다.
다른이 풀이
from sys import stdin
input = stdin.readline
T = int(input())
answer = ""
result = [False, False, True] + [True, False] * 5000
for number in range(3, 101, 2):
if result[number]:
result[number*2::number] = [False] * len(result[number*2::number])
for tc in range(T):
N = int(input())
if N == 4:
answer += "2 2\n"
continue
harf_N = N//2
if not harf_N % 2:
harf_N += 1
for i in range(harf_N, N, 2):
if result[i] and result[N-i]:
answer += "{} {}".format(N - i, i) + "\n"
break
print(answer, end="")

최고