빅오(big-O) : 알고리즘, 누가 누가 빠르지?

본 글은 박상길 저자의 파이썬 알고리즘 인터뷰 책을 학습 및 참고하여 정리한 내용임을 밝힙니다.

빅오(big-O)란 입력값이 무한대로 향할때 함수의 상한을 설명하는 수학적 표기 방법이다.
박상길, 『파이썬 알고리즘 인터뷰』, p100

위와 같은 교과서적인 정리는 가슴에 쉽게 와닿지 않는다. 따라서 쉽고 간단한 예시를 통해 빅오(big-o)가 무엇이고 어떻게 표현되는지 알아보도록 하자

빅오(big-o)에 대한 간단한 이해

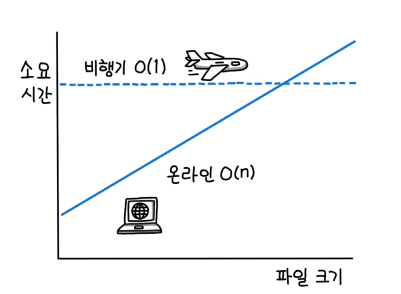
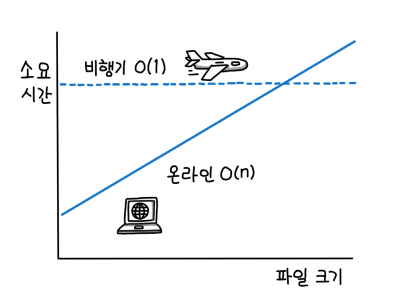
위와 같은 그래프를 보고 이야기를 해보도록 하자
우리가 갖고 있는 데이터를 다른 곳에 살고 있는 친구에게 보낸다고 할 때 위 그래프는 다음과 같다.

• y축 : 데이터를 보내는 소요 시간
• x축 : 파일의 크기

1. 입력값 n이 아주 작을 때를 고려해보자!

데이터의 크기가 아주 작다면 $O(n)$이 걸리는 온라인 배송이 $O(1)$이 걸리는 비행기 배송보다 소요 시간이 짧다. 하지만, 알고리즘은 실제로 컴퓨터로 구현되므로 n의 크기가 작다면 어떤 알고리즘이더라도 금방 끝날 것이다. 따라서 우리가 고려해야되는 점은 입력값 n이 충분히 클 때 알고리즘 효율성에 따른 소요 시간이다.

2. 입력값 n이 무한대로 향할 때를 고려해보자!

입력값 n이 아주 작을 때와는 반대로 n이 무한대로 커질 때 온라인을 통한 데이터 전송은 온라인 배송보다 소요 시간이 더 커지는 것을 알 수 있다. 데이터의 크기가 아무리 커져도 비행기를 통한 배송은 O(1)로 소요 시간이 고정되어 있는 반면 온라인 전송은 $O(n)$로 선형적으로 증가하기 때문이다.

이것이 바로 점근적 실행 시간이며, 빅오(big-o)는 점근적 실행 시간을 표기하는 방법 중 하나다

이때 $O(n)$의 의미는 입력값만큼 실행 시간에 영향을 받으며, 알고리즘 수행하는데 걸리는 시간은 입력값에 비례한다라는 의미이다.

빅오(big-o)와 코딩

초보 개발자로서 내가 작성한 문제 풀이와 알고리즘 코드들이 좋은 코드인가에 대해 많은 고민을 하였다.
그렇다면 좋은 코드란 무엇일까?

내가 정의한 좋은 코드란 다음 두 가지 조건을 만족할 수 있는 코드이다.

1. 코드의 가독성이 뛰어나다.
2. 알고리즘의 효율성이 뛰어나다.

여기서 2. 알고리즘의 효율성이 뛰어나다. 를 어떻게 분석할 수 있을까?

우리는 알고리즘의 효율성을 얼마나 많은 시간을 소요하는지, 얼마나 많은 메모리를 필요로 하는지를 통해 추정할 수 있다.

이때 여기서 말하는 '얼마나 많은 시간을 소요하는지'가 위에서 말한 점근적 실행 시간이며 이를 다른 말로 시간 복잡도(Time Complexity)라고 표현하고 이를 표기하는 대표적인 방법이 바로 빅오이다.

• 점근적 실행 시간 == 시간 복잡도 == 빅오(big-o)

빅오 표기법

빅오로 시간 복잡도를 표현할 때는 최고차항만을 표기하며, 계수는 무시한다.
ex) $4n^2+4n+1 => O(n^2)$
이처럼 시간 복잡도를 표기할 때는 입력값에 따른 알고리즘 소요 시간의 대략적인 추이만을 살핀다.

빅오 표기법의 종류는 크게 다음과 같다.

1. $O(1)$
   입력값이 아무리 커도 실행 시간이 일정한 최고의 알고리즘이다. 하지만 상수 시간에 실행된다 해도 상수값이 상상을 넘어설 정도로 매우 크다면 의미가 없다.

   『예시』
   해시 테이블의 조회 및 삽입
   

2. $O(log n)$
   실행 시간이 입력값에 영향을 받지만 로그는 매우 큰 입력값에도 크게 영향을 받지 않는 편이다.

   『예시』
   해시 테이블의 조회 및 삽입
   

3. $O(n)$
   입력값만큼 실행 시간에 영향을 받으며, 입력값과 소요 시간이 비례한다. 이를 선형 시간 알고리즘이라고 한다. 값을 찾기 위해 모든 입력값을 적어도 한 번 이상은 살펴봐야하는 알고리즘이 이에 포함된다.

   『예시』
   정렬되지 않은 리스트에서 최댓값 또는 최솟값을 찾는 경우
   

4. $O(n log n)$
   대부분의 효율 좋은 정렬 알고리즘이 이에 해당된다. 적어도 모든 수에 대해 한 번 이상은 비교해야 하는 비교 기반 정교 알리고리즘은 아무리 좋아도 $O(nlogn)$ 보다 빠를 수 없다.

   『예시』
   병합 정렬
   

5. $O(n^2)$
   주로 비효율적인 정렬 알고리즘이 이에 해당된다.

   『예시』
   버블 정렬
   

6. $O(2^n)$
   피보나치 수를 재귀로 계산하는 알고리즘이 이에 해당 된다.