FITS

What To Solve

• 시계열 데이터를 효율적으로 분석하기 위해 제안된 경량화된 모델
• 시계열 데이터의 복잡성과 동적 특성을 효과적으로 분석할 수 있는 경량 모델의 개발

How To Solve

• Interpolation in the Complex Frequency Domain:

  • 시간 도메인에서의 복잡한 시계열 데이터를 주파수 도메인으로 변환
  • 변환된 데이터는 복소수로 표현되며, 이는 진폭과 위상 정보를 포함
  • 이 복소수 주파수 데이터를 보간하여 주어진 시계열 데이터의 확장된 또는 예측된 값을 생성

• Lightweight Model Structure:

  • FITS는 복소수 신경망을 사용하여 주파수 도메인에서 보간을 수행
  • Low-Pass Filter를 사용하여 모델 크기를 줄이고, 필수적인 정보만 유지

• 10k parameter로 시계열 모델링이 가능한 모델.

Contributions

• 기존 : Raw time-series 처리
• FITS : complex frequency domain에서 interpolation 을 통해 시계열 처리
• Frequency domain에서 complex interpolation을 사용해서 forecasting , reconstruction 작업 수행.

What is Complex interpolation

• 시계열 데이터: 잡음과 복잡한 패턴으로 구성됨.
• Time-domain 에서 직접적인 예측이나 재구성은 어려울 수 있음.
• frequency-domain에서는 신호의 주파수 성분이 보다 명확하게 나타나기 때문에, 주파수 도메인에서 보간을 통해 시계열 데이터를 처리하면, 이러한 복잡성을 줄고 보다 정확한 예측 및 재구성 가능

frequency domain의 time-series model들과 의 차이점 :

• 기존 모델들(FEDformer,FiLM): 주파수 도메인 정보를 보조 기능으로 활용하거나 주기성을 포착하는 데 중점
• FITS는 주파수 도메인에서 직접적인 interpolation을 통해 시계열 신호 처리
  - 모델 크기와 복잡성: FITS는 매우 경량화된 구조로, 기존 모델들에 비해 훨씬 적은 파라미터로 작동
  - 복소수 신경망: FITS는 복소수 신경망을 사용하여 주파수 도메인에서의 보간을 수행하므로, 진폭과 위상 정보를 동시에 학습하고 처리함.

BiaTCGNet

What To Solve

• 결측된 시계열 데이터의 예측: 실제 세계의 시계열 데이터는 종종 결측치를 포함하게 되며, 이러한 결측 데이터에서도 정확한 예측을 수행하는 것이 목표입니다.

How To Solve

• 기존 접근 방식의 한계: 기존 방법들은 결측치를 보정한 후 예측하는 두 단계 접근 방식을 사용하며, 이로 인해 오차가 누적되어 성능이 저하
• Graph를 이용한 시간적 및 공간적 정보 통합: BiTGraph 모델은 시계열 데이터의 시간적 의존성과 공간적 상관관계를 모두 고려하여 예측을 수행
  - Multi-Scale Instance PartialTCN: 여러 시간 스케일에서 부분적으로 관측된 데이터를 처리하여 각 인스턴스의 시간적 의존성을 캡처
  - Biased GCN: 결측치 패턴을 반영한 편향된 그래프 신경망을 사용하여 인스턴스 간의 공간적 상관관계를 모델링
  - 결측치 패턴을 반영하여 예측 성능을 향상시킴

TimeMixer

What To Solve

• LTSF

How To Solve
서- 로 다른 샘플링(multi-scale) 스케일로 시계열 데이터 분해 (뚜렷한 패턴을 보여줌.)

• MLP 기반의 구조
  - Past Decomposable-Mixing (과거)
  - 시계열 데이터를 multi scale로 분해한 뒤 각 스케일의 계절적 추세적 성분을 분리 하여 각각 미세한 정보와 거시적인 정보를 성공적으로 결합함.
  - 미세한 정보 : 세밀한 변동 / 거시적인 정보 : 추세
  - Future Multipredictor-Mixing (미래)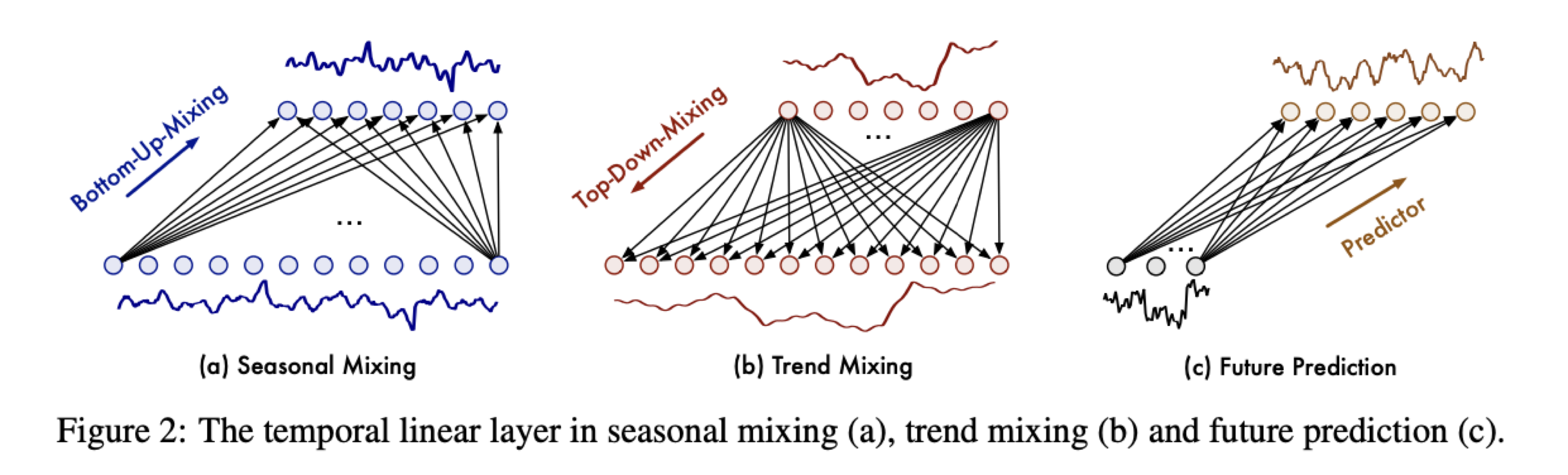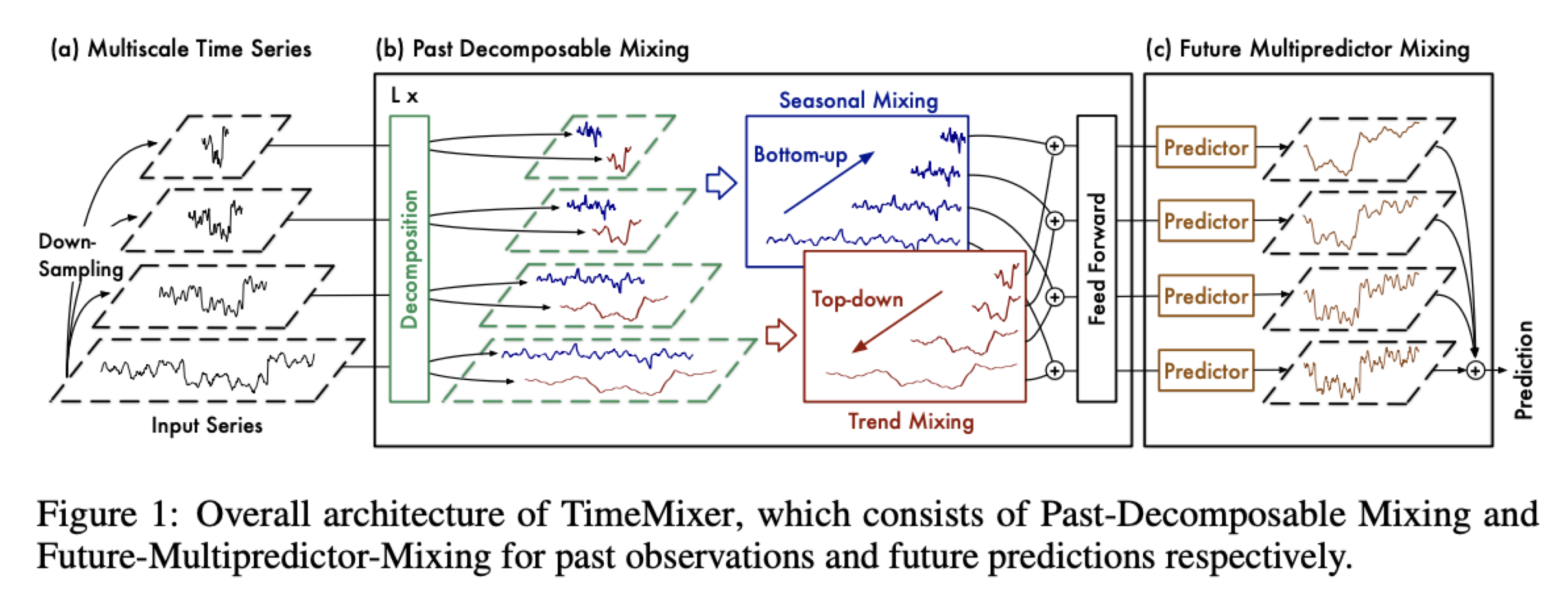

  ![](https://velog.velcdn.com/images/sheoyonj/post/526c40fe-cd0c-4e21-9163-5ad312a10098/image.png)

  

Looped Transformer

What To Solve

• Transformer 모델이 반복적인 학습 알고리즘을 효과적으로 모방하도록 하는 새로운 방법론 제안

How To Solve

• 루프 아키텍처: 루프 트랜스포머는 반복적인 구조이며, 모델이 동일한 입력을 여러 번 처리하면서 점진적으로 성능을 향상시키도록 함.
  - 이 과정은 특정 반복 횟수 이상에서는 성능이 더 이상 향상되지 않고 고정된 값을 유지하는 '고정점'에 도달함.
• Input Injection: 각 반복 단계에서 입력을 다시 모델에 주입하여, 초기 입력의 영향을 유지하고 성능의 저하를 방지.
  - 이를 통해 Looped Transformer는 반복적인 처리 과정에서 입력 정보가 희석되는 문제를 해결함.
  

Contribution:

• Looped Transformer 는 반복적인 학습 알고리즘을 효과적으로 모방할 수 있으며, 이를 통해 트랜스포머의 데이터 적합 문제 해결 능력을 향상시킬 수 있음.
• 이 방법은 모델의 매개변수를 절약하면서도 높은 성능을 유지함.
• 이 논문은 반복적인 알고리즘을 트랜스포머 아키텍처 내에서 구현하는 방법에 대한 새로운 접근을 제시하며, 향후 다양한 기계 학습 문제에 적용될 수 있는 가능성 보여줌.