안녕하세요! 저는 최근에 MY BASEBALL ✪ ALL STAR 를 성공적으로 릴리즈 했어요
주위에 야구 좋아하는 친구들이 재미있다는 말을 많이 해 줘서 아주 뿌듯했습니다
그런데 생각보다 최종 팀 점수를 랜덤이라고 생각하시는 분들이 많더라고요?
지피티 기반이라는 의혹을 블로그 글을 통해 설명해 드리려고 찾아왔습니다
왜냐하면 이렇게나 열심히 구현했거든요
나는 진심이었어...
기존 로직
저희는 개발자 총 2명으로 해당 프로젝트를 진행했어요
팀 점수 구현에 관한 부분은 두 명 모두가 관여하였는데
다른 개발자 친구가 기록지를 통해 크롤링하여 선수 점수로 변환하는 로직을 담당하였고,
제가 해당 선수 점수를 바탕으로 팀 점수를 만드는 로직을 구현하였어요

구현을 끝내고 테스팅을 해 보는 과정에서 저는 이런 카톡을 받았습니다
저는 분명 0점에서 100점 사이 선수들의 점수가 들어오면
이것을 0점에서 15점 사이의 팀 점수로 변환하는 코드를 작성하였는데 왜 이렇게 된 것일까요?
문제점 파악
저는 구현 당시에 선수들의 점수가 0점부터 100점까지 고르게 퍼져있다는 가정 하에 코드를 구현하였어요
따라서 선수의 점수를 합산하고 선택 횟수 가중치를 log로 적용해서 평균을 내는 과정이었어요
log를 취한 이유는 제가 이번 강의 시간에 정보 검색 강의를 들었는데
값 자체를 가중치에 적용하면 그 폭이 너무 커져서
휴리스틱하게 로그를 취하는 게 보편적으로 사용하는 방식이더라고요
그 방식이 강의 듣는 내내 합리적이라는 생각이 들어 저 또한 차용하였습니다
다시 돌아가, 제가 구현한 코드에서의 문제점은 0점부터 100점까지 고르게 퍼져있다는 가정이었어요
실제로 크롤링 후 변환된 데이터를 분석해 보니
54.66, 35.16, 61.5, 45.55, 43.21, 63.71, 53.66, 75.35, 66.41, 55,
20.16, 29.08, 26.59, 38.42, 19.92, 24.09, 26.7, 26.33, 27.68, 15.94,
22.05, 34.08, 33.01, 41.14, 38.2, 29.74, 20.18, 39.44, 22.72, 30.43,
40.13, 45.29, 38.37, 34.58, 37.69, 34.36, 44.85, 37.88, 39.1, 31.38,
54.18, 36.98, 34.14, 39.37, 38.77, 47.31, 47.72, 44.29, 46.09, 38.31,
36.61, 33.31, 37.05, 32.04, 37.26, 36.42, 37.36, 33.11, 39.85, 31.9,
37.06, 35.41, 34.9, 38.77, 33.96, 43.44, 45.4, 43.2, 34.27, 44.03,
39.21, 37.72, 32.21, 37.32, 37.06, 36.78, 36.23, 31.46, 36.76, 34.89,
43.79, 37.33, 35.16, 34.1, 45.37, 36.08, 35.24, 34.73, 36.97, 36.38,
39.6, 41.67, 33.11, 35.77, 38.71, 33.88, 34.17, 39.18, 34.47, 31.5,
34.16, 35.1, 41.68, 36.81, 34.84, 33.73, 33.81, 38.73, 38.12, 38.17,
42.17, 38.35, 50.59, 40.96, 41.37, 47.29, 42.12, 42.97, 37.29, 32.74이런 식의 점수 분포를 보였습니다 점수를 자세히 살펴 보면 주로 30-40점에서 머무는 것을 확인할 수가 있어요
이것 때문에 점수가 7점 혹은 8점으로 편향될 수밖에 없다는 사실을 발견했습니다
팀 점수 시뮬레이터 구현
저는 같은 실수를 방지하기 위해 팀 점수 시뮬레이터를 우선 구현하고
이후 로직을 수정하기로 하였습니다
팀 점수가 고르게 나오는지 확인할 수 있는 시뮬레이션을 돌리는 로직인데요
선수 선택에 따라 팀 점수가 다양하게 나오는 것이 목표이기 때문에
정해진 SIMULATION_COUNT만큼 팀을 랜덤으로 만들어서 점수를 확인할 수 있는 간단한 로직입니다
해당 구현에서 저의 목표는 점수가 0점부터 15점까지 고르게 나오는 것이었습니다
public class TeamScoreSimulation {
private static final int SIMULATION_COUNT = 1000;
private static final double[] PLAYER_SCORES = {선수들 점수 삽입};
public static void main(String[] args) {
Map<Integer, Integer> scoreDistribution = new TreeMap<>();
Random random = new Random();
for (int sim = 0; sim < SIMULATION_COUNT; sim++) {
// 무작위로 12명 선택
List<Integer> indices = IntStream.range(0, PLAYER_SCORES.length)
.boxed()
.collect(Collectors.toList());
Collections.shuffle(indices);
List<Integer> selected = indices.subList(0, 12);
// 무작위 choice count (1~10)
List<Long> choiceCounts = selected.stream()
.map(i -> (long) (random.nextInt(10) + 1))
.collect(Collectors.toList());
// 점수 추출
List<Double> selectedScores = selected.stream()
.map(i -> PLAYER_SCORES[i])
.collect(Collectors.toList());
// 팀 점수 계산
int teamScore = TeamScoreCalculator.calculate(selectedScores, choiceCounts);
// 분포 기록
scoreDistribution.put(teamScore, scoreDistribution.getOrDefault(teamScore, 0) + 1);
}
// 결과 출력
System.out.println("Team Score Distribution:");
for (Map.Entry<Integer, Integer> entry : scoreDistribution.entrySet()) {
System.out.printf("%2d : %s (%d)%n", entry.getKey(),
"*".repeat(entry.getValue() / 10), entry.getValue());
}
}
}이것을 구현한 직후에 현재 점수 set으로 시뮬레이션을 돌려보니

진짜 7점과 8점만 나올 수밖에 없는 구조였고 이를 개선해 보겠습니다
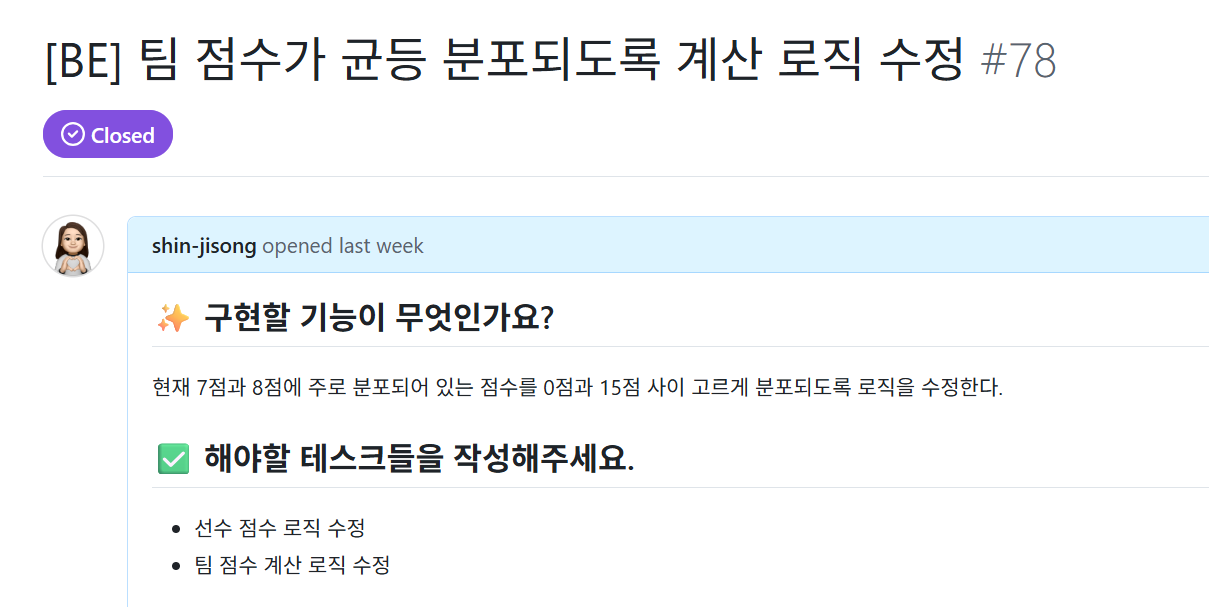
팀 점수 로직 변경
저는 팀 점수 로직을 변경해 이 문제를 해결해 보려고 하였습니다
여기서 전제가 필요했습니다
계산마다 DB에서 모든 Player의 점수 set을 읽는 로직은 성능적으로 합리적이지 않기에 지양하고 싶었어요
따라서 선수단의 점수들을 모른다는 가정하에 구현할 것, 그러나 0점부터 100점까지의 분포는 알고 있을 것이었습니다
첫 번째 시도
이를 위해 간단한 방식으로는, 먼저 비선형 함수를 도입하는 방법이 있습니다 예를 들어, 선수 점수를 단순히 평균 내는 것이 아니라, 각 점수에 제곱근(sqrt)과 같은 함수를 적용하면 결과 분포가 더 넓게 퍼지게 됩니다 이렇게 하면 대부분 7~8점에 몰리던 팀 점수가 좀 더 다양해질 수 있습니다
또 다른 방식은 logit 함수를 이용하는 것입니다 logit은 점수를 0에서 1 사이로 정규화한 후, 이 값을 넓은 범위로 다시 펼쳐주는 역할을 하는 함수로, 특히 중간 점수대에 몰린 분포를 효과적으로 분산시킬 수 있습니다
마지막으로, 계산된 점수에 작은 무작위성(노이즈)을 추가하는 방법도 있습니다. 예를 들어 동일한 조건의 팀이라도 점수 계산 과정에 ±5% 정도의 흔들림을 주면, 같은 7점대에 머무르지 않고 6점 또는 8점 등으로 자연스럽게 분산되는 결과를 얻을 수 있습니다
저는 이 중에서 logit 변환을 각 선수 점수에 개별적으로 적용한 방식을 도입했습니다 즉, 12명의 선수 각각의 점수를 logit 함수로 변환하고, 이를 평균 내어 팀 점수를 계산하는 방식입니다 이렇게 하면 한 팀 안에 0점짜리 선수와 15점짜리 선수가 섞여 있을 경우, 팀 점수도 그 영향을 반영하여 보다 다양하게 나타날 수 있습니다
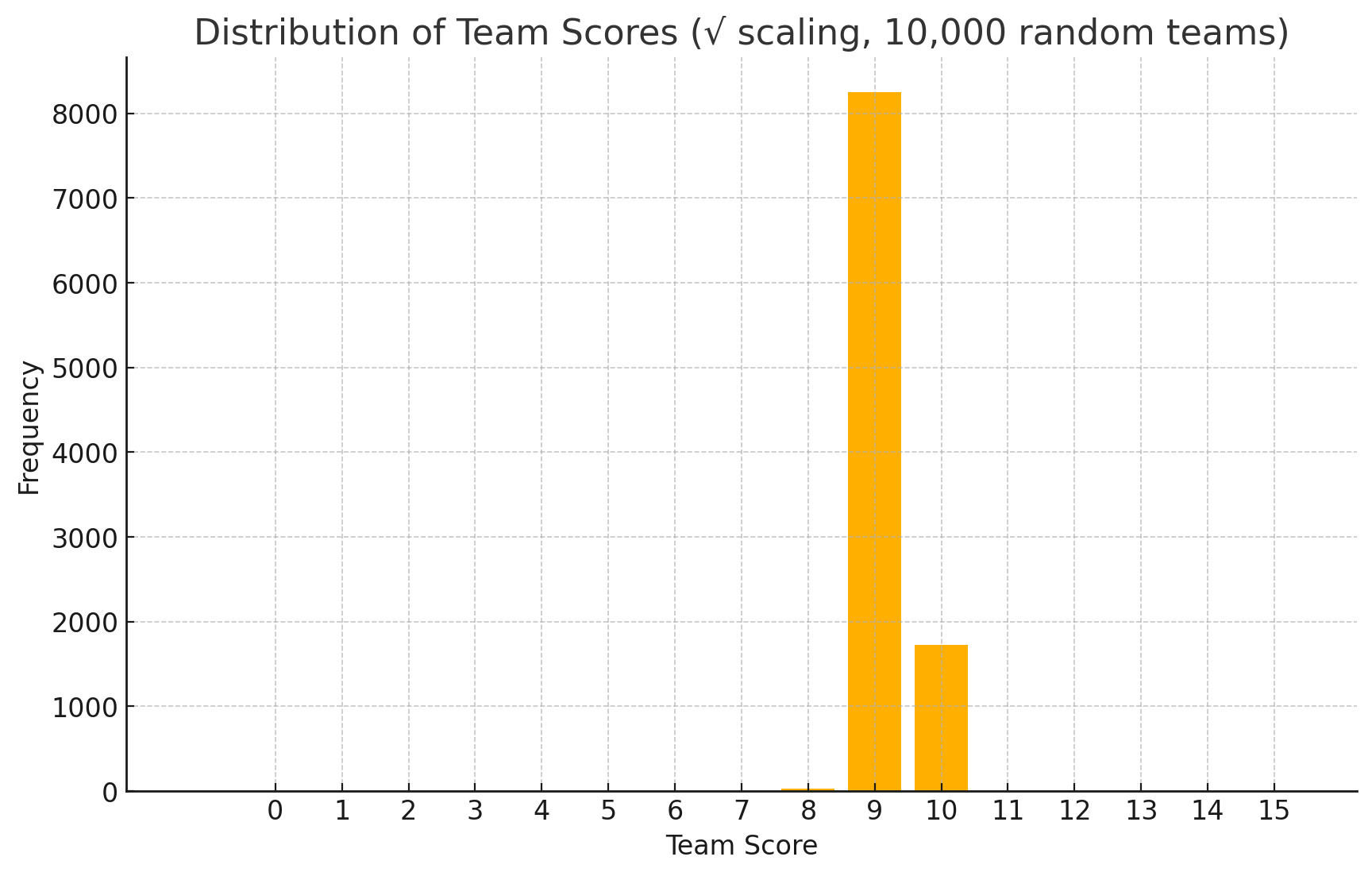
하지만 효과는 미미했어요... 워낙 좁은 범위로 분포해 있는 로직이라 분산시키기가 쉽지 않았습니다
두 번째 시도
다음 시도 방식으로 Z-score + 시그모이드 정규화 방식을 도입하였습니다
Z-score 정규화는 특정 선수의 점수가 전체 분포(평균과 표준편차 기준)에서 얼마나 떨어져 있는지를 수치화하는 방식입니다 예를 들어, 어떤 선수가 평균보다 두 표준편차만큼 높다면 Z-score는 +2가 되고, 평균보다 한 표준편차만큼 낮다면 -1이 됩니다 이렇게 하면, 각 선수의 점수를 전체 분포 속에서 상대적인 위치로 바꿔 표현할 수 있습니다
그러나 Z-score는 정규화된 값이 -∞부터 +∞까지 나올 수 있어, 점수 시스템에 바로 사용하기에는 다소 불편합니다 이를 해결하기 위해, Z-score 결과에 시그모이드 함수를 적용하였습니다. 시그모이드는 입력값을 부드럽게 0과 1 사이로 압축해주는 함수로, 크거나 작은 극단적인 값을 자연스럽게 누르며, 중앙값(평균에 해당하는 Z=0)을 기준으로 0.5 근처에 위치시켜줍니다
이 과정을 통해, 전체 점수 분포의 형태는 고려하면서도 선수들의 실제 점수 배열을 몰라도 상대적인 위치에 따라 정규화된 값을 계산할 수 있게 되었습니다 또한 시그모이드의 특성 덕분에 이상치의 영향력이 완화되고, 정규화된 점수는 팀 점수 계산에 바로 사용할 수 있을 정도로 안정적인 범위를 갖게 됩니다
즉, 이 방식은 정규 분포를 가정한 점수 환경에서, 데이터셋 전체를 알 수 없는 상황에서도 각 선수의 점수를 안정적이고 비교 가능하게 정규화할 수 있는 합리적인 대안이었습니다

하지만 이 또한 결국 극단적인 값을 눌러주는 효과만 있어 분포의 효과는 없었습니다
선수 점수 로직 변경
위 시도 외에도 여러 시도를 하였지만 모두 점수를 다양하게 펼치는 것에는 실패하였습니다
저는 선수 점수가 좁게 한정되어 있고, 해당 점수 set을 모르는 가정이라면
팀 점수를 고르게 분포시키는 것은
학부 시절 배운 데이터 분석의 지식으로는 어렵겠다는 결론을 내렸습니다
따라서 선수 점수가 특정 범위 내에 고르게 분포해 있다는 가정 하에 해당 로직을 작성하기 위해 선수 점수 로직을 변경하였습니다
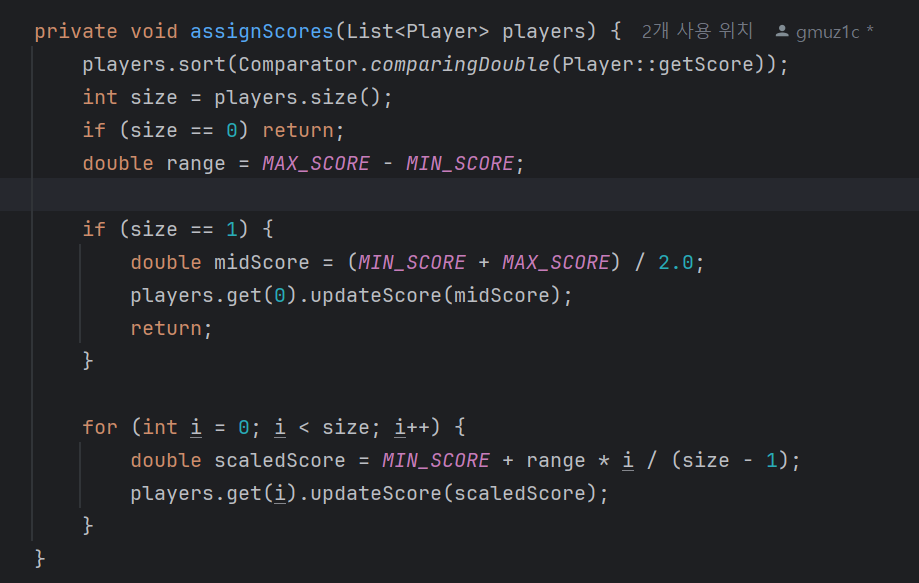
이런 로직을 구현하여 크롤링 이후 선수의 점수가 업데이트 되면
그 점수를 바탕으로 정렬하여
최소 점수부터 최고 점수까지 일정 간격을 적용하여 점수를 부여하였습니다
이를 통해 저는 원하는 범위 내에서 일정한 간격의 점수를 부여했다는 전제로
팀 점수를 구현할 수 있었습니다
변경된 선수 점수 로직을 바탕으로 팀 점수 구현
팀 점수 산정은 개별 선수들의 점수를 일정한 범위 내에서 정규화한 뒤, 선택 확률에 따라 무작위로 한 명의 점수를 뽑아 대표 점수로 사용하는 방식으로 구현했습니다.
처음에는 모든 선수들의 점수를 평균 내거나, 단순히 선택 횟수에 가중치를 곱하는 등의 방식도 고려했지만, 이러한 방식은 특정 구간의 점수대가 지나치게 몰리며 중앙값 근처에 치우친 종 모양(산 모양)의 분포를 만들게 됩니다

실제 정규화 이후 가중치만을 적용하니 다음과 같은 시뮬레이션 결과가 나왔습니다 🥲
선수들의 원 점수는 기본적으로 일정한 범위를 가지지만, 이 점수들을 가중치 없이 혹은 비율 기반 평균으로 계산할 경우, 결과값은 자연스럽게 중앙에 몰리는 경향을 띕니다. 특히 평균, 가중 평균, 중간값 기반 계산 로직은 통계적으로 정규분포(또는 유사 정규분포)를 유도하는 특성을 가지기 때문에, 극단적으로 높은 점수나 낮은 점수가 선택될 확률은 희박해지고, 대부분의 결과가 중간 점수대에 집중되는 결과가 나타납니다
하지만 제가 의도한 점수 시스템은 0점부터 15점까지의 구간에서 점수가 고르게 분포되는 구조였습니다 즉, 특정 점수대에 집중되는 쏠림 없이, 전체 점수 범위가 비교적 균등하게 사용되기를 원했습니다
이를 위해 저는 먼저 선수 개별 점수를 일정한 간격의 정수값으로 정규화하여 0~15 범위로 매핑하고, 여기에 선택 확률 기반의 선택 횟수 로직을 적용함으로써, 원시 점수의 절대값보다는 사용자 선택 횟수에 비례하여 각 점수가 대표 점수로 선택될 수 있도록 설계했습니다
이렇게 함으로써, 단순 평균 방식에서 발생하는 산 모양의 점수 분포를 피하고, 0~15 사이의 다양한 점수들이 고르게 분포될 수 있도록 유도할 수 있었습니다 이는 곧 제가 설계한 시스템이 보다 균형 잡히고 예측 불가능성을 유지한 점수 산정을 가능하게 했다는 점에서 의미가 있습니다
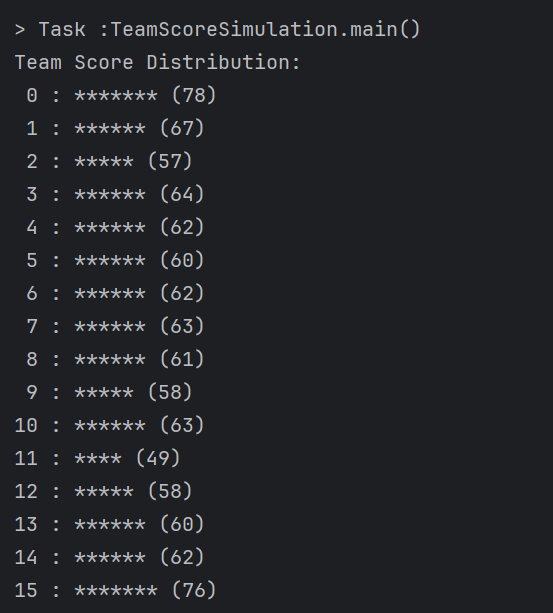
실제 시뮬레이션 결과를 보니 제가 의도했던 0점부터 15점까지 고르게! 를 구현할 수 있었어요
마무리
구현하는 데 정말 힘들었지만 이를 적용 후 플레이를 해 보니

이렇게 고르고 다양한 결과가 나오더라고요
이런 결과 덕에 AI 의심을 받았지만 그만큼 잘 분포돼 있는,
노력을 더한 코드였습니다
다들 즐겁게 플레이 해 주세요 ⚾
