📑문제
처음 시작 도시에서 끝 도시까지 최소한의 기름비용으로 가기 위한 최적의 방법은?
💡 핵심 포인트
최소 비용으로 가려면 어떻게하지?
처음 문제를 봤을 때 아이디어가 아예 떠오르지 않았다. 이걸 어떻게 풀어야하나 싶은 생각이 들어 그림판에 그려놓고 프로그래밍을 떠나서 내가 이걸 푼다면 어떻게 풀까 싶어서 내 뇌로 문제를 풀려고 해보았다. 그렇게 하니 갈피나 특징? 이라 할 것들이 잡히기 시작했다.
-
첫 시작 지점에서는 기름값이 얼마나 비싸던 최소 다음 도시 거리까진 사야한다.
-
가격을 최소로 잡을려면 기름값이 가장 싼 곳에서 살 수 있는만큼 구매해서 도시를 이동해야한다.
최소 가격으로 여러 번 반복하자
가격이 최소가 되는 부분을 찾고 그 곳에서는 남은 거리까지의 거리에 대해 몽땅 기름을 사서 가면 되는 부분이다. 하지만 항상 최소 가격의 주유소가 앞에 존재하는 법은 없다. 그렇기에 최소 가격의 주유소에서 최종 도시까지 기름을 살 계획을 세웠다면, 최소 가격 주유소를 다시 최종 도시로 잡고 다시 최소 가격의 주유소를 찾아 반복을 돌리는 것이다.
큰 흐름은 잡았으나 그것을 코드로 만들려고 하니 반복문 조건, 변수 값 등 많은 것들에 대해 생각을 하니 생각보다 문제를 해결하기 쉽지 않았다.
❗ 오류수정
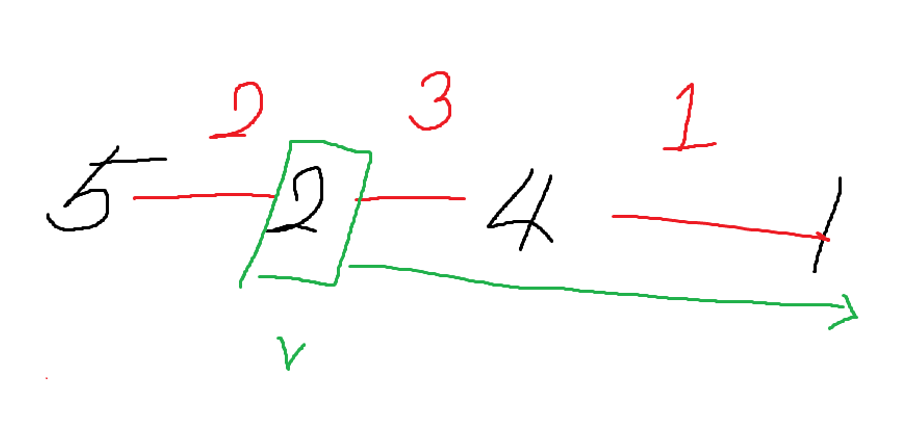
여러 번 코드를 수정하고 그림을 다시 그려보며 문제는 맞았지만 서브 태스크 문제였고, 배점 17, 41점을 맞고 42점 배점은 조건을 맞추지 못하여 결과적으로 애매하게 푼 문제이다.
첫 번째 제출에서는 VS에서 실행 했을 때는 주유소 가격이 모두 일치하는 경우도 값이 잘 나왔지만 맞았다고 체점되지 않아서 혹시나 싶어 배열의 크기를 늘려보니 맞는 걸로 채점이 되었다. 마지막 문제는 원래의 제약조건 이외에 아무 제약조건이 없다. 인데 정확히 무엇을 의미하는지 잘 모르겠어서 코드를 조금 정리 후 마무리 하였다.
❗ 느낀점
요즘 들어 고전하게 되는 문제가 많다. 당연하게도 브론즈 문제에서는 어렵다 싶어도 몇 개를 제외하곤 30분 이상 큰 고민을 한 문제가 없었다. 하지만 최근에 풀고 있는 그리디 알고리즘은 최적의 경우의 수를 찾기 위해 뭔가 머리를 많이 굴려야 하는 것 같다. 심지어 문제는 맞게 풀긴 했는데 이게 가장 최적으로 푼 것 같은 생각은 들지 않고 무언가 다른 좋은 방법이 있을 것 같긴하다.
이번에 나름 노력한 부분은 코드가 조금 길어지다보니 주유소 가격이 모두 똑같은 경우는 구현한 함수를 이용하여 코드를 구성하였다.
🧾 전체 코드
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
int Gas_Same(int* Gas, int city);
int main()
{
int City = 0;
int Distance[10000000];
int Gas[10000000];
int Sum_Price = 0;
int T_Distance = 0;
scanf("%d", &City);
int Move_index = City;
int Keep = City - 1;
//도시 사이 거리 입력
for (int i = 0; i < City - 1; i++)
{
scanf("%d", &Distance[i]);
}
//도시의 가스 가격 입력
for (int i = 0; i < City; i++)
{
scanf("%d", &Gas[i]);
}
//만약 모든 도시 가스비가 똑같다면?
if (Gas_Same(Gas, City - 1))
{
for (int i = 0; i < City - 1; i++)
{
T_Distance += Distance[i];
}
Sum_Price = Gas[0] * T_Distance;
}
else
{
while (Move_index != 0)
{
T_Distance = 0;
int Min_Gas = Gas[0];
//최소 가스 가격을 찾아낸다.
for (int i = 0; i < Move_index; i++)
{
if (Gas[i] < Min_Gas && i != City - 1)
Min_Gas = Gas[i];
}
//최소 가격이 어느 도시인지
for (int i = 0; i < Move_index; i++)
{
if (Min_Gas == Gas[i])
Move_index = i;
}
//거리 측정 최소로 -> 남은 거리만큼 몽땅 사서간다
for (int i = Move_index; i < Keep; i++)
{
T_Distance += Distance[i];
}
//printf("%d 가스로 이동할 거리 : %d\n", Min_Gas, T_Distance);
Sum_Price = Sum_Price + (Min_Gas * T_Distance);
//printf("Keep : %d, Sum : %d\n", Keep, Sum_Price);
Keep = Move_index;
}
}
printf("%d", Sum_Price);
}
int Gas_Same(int* Gas, int city)
{
for (int i = 0; i < city; i++)
{
if (Gas[i] != Gas[i + 1])
{
return 0;
}
}
return 1;
}