📝DP : 개념
DP는 Dynamic Programming의 준말로 동적 프로그래밍
- 복잡한 문제를 간단한 여러 개의 문제로 나누어 해결
- 조건 1 : 부분 반복(같은 부분이 여러 번 사용된다)
- 조건 2 : 최적 부분(작은 부분 문제를 쌓아 큰 답을 구할 수 있다)
DP에 대해 학습하면서 가장 중요한 키워드는 기록memo이었다.
DP란 개념 존재 자체의 이유가 중복된 데이터 처리를 막기 위함인데, 이에 관련된 가장 대표적인 예시로 피보나치 수열이 존재했다.
DP : 예시로 이해하자
피보나치 수열은 F(n) = F(n-1) + F(n-2) 이다.
함수 그대로를 보면 현재 우리가 구하고 싶은 n을 위해 이전 단계의 n-1, n-2 가 필요하다는 것이고 만약 우리가 F(n)를 구하고 싶다면
F(5) = F(3) + F(4)
근데 F(3) = F(2)+F(1), F(4) = F(2)+F(3)
이런 식으로 밑 단계를 구하기 위해서 반복적으로 필요한 숫자들이 존재하고, 이를 불필요하게 계산을 해야한다는 점이다.
단순하게 우리가 피보나치 수열을 이런 재귀함수로 구현했다면
Fibo(n):
if(n == 1) : return 1
if(n == 2) : return 1
return Fibo(n-1) + Fibo(n-2)F(50)인 경우 50부터 시작해 한 가지씩 내려갈 때마다 2씩 곱해져버려서 2의50제곱, 2의 10제곱이 1000이니 000 * 5 즉 0이 15개나 있는 엄청난 큰 수를 구해야하는 것이다.
계속적으로 불필요한 작업을 하니 이것을 간단히 해결할 수 있는 방법이 DP이다.
그럼 DP를 이용해 이 문제를 해결한다면?
Fibo_ary = [ 0 for i in range(100)]
Fibo(n):
if(n == 1) : return 1
if(n == 2) : return 1
if(Fibo_ary[n]) return Fibo[n]
return Fibo(n-1) + Fibo(n-2)문제풀이
[S1]10844] 쉬운 계단 수
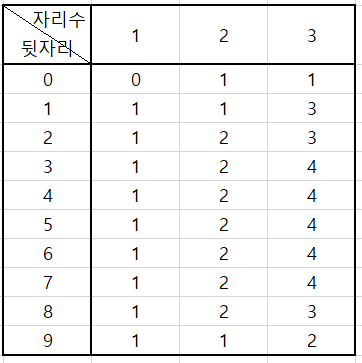
DP로 문제를 풀 수 밖에 없는 것이 자리수가 최대가 100자리 였기 때문에 순수 계산만으로 이 문제를 해결할 수 없다는 것을 알았다. 그러나 어떠한 방식으로 DP를 풀 수 있을지 아이디어가 잘 떠오르지 않았고 그림판에 숫자를 끄적이며 어떤 방식으로 숫자가 만들어질지 적어보다보니 자리수가 2자리라면 끝에 0,1,9를 제외하고는 전부 2개가 올 수 있었고 3자리가 되다보니 앞의 경우에 연장선으로 4개로 증가하는 것을 보고 무언가 규칙이 있겠다 싶어 엑셀에 차례로 정리를 해보았다.
뭔가 규칙이 보이는 것 같은데 잘 모르겠어서 서칭을 해서 아이디어를 참고하니 식이 보였고 그대로 코드를 작성했다.
DP의 첫 문제라 그런지 매우 어렵고 아이디어를 떠올리는 것 자체가 너무나도 오래 걸리고 힘들었다.
import sys
input = sys.stdin.readline
n = int(input())
# 한 행에 10개를 담을 수 있고, n개의 열(자리수) 만들기
dp = [[0] * 10 for i in range(n + 1)]
for i in range(1, 10):
dp[1][i] = 1
for i in range(2, n+1):
for j in range(10):
if j == 0:
dp[i][j] = dp[i-1][1]
elif j == 9:
dp[i][j] = dp[i-1][8]
elif j >= 1 and j < 9:
dp[i][j] = dp[i-1][j-1] + dp[i-1][j+1]
all_num = int(sum(dp[n]) % 1000000000)
print(all_num)[G5]12865] 평범한 배낭
원래 문제를 풀면 그 아이디어 그대로 그냥 쭉 코드를 짜보고 안되면 다시 다른 방법을 생각하고 풀어보고 이런 방식으로 진행을 했다.
하지만 여러 알고리즘을 풀면서 내가 논리 자체를 잘못 접근하는 경우가 빈번하게 발생하여 애초에 해당 문제를 풀 때 어떻게 풀 지 생각을 하고 주석으로 아이디어들을 적어보고 해당 아이디어를 어떻게 풀어나갈지 까지 생각하고 문제를 풀어보았다.
📌시도 1
아래 주석에서 보다싶이 여러 방법을 생각했고, 이 문제는 모든 경우의 수를 탐색하고 마지막에 가치를 생각해보는 것을 틀로 잡고 접근하였다.
이렇게 큰 틀을 잡고 시작을 하니 뭔가 어렵지 않게 문제를 풀었고 어라..내가 골드 문제를 이렇게 쉽게 풀었다고? 하면서 성취감과 뿌듯함이 들었고 제출을 하니..틀렸다 문제 요구에 맞는 정답이 출력되는데 시간 초과도 아니고 아예 틀렸다고 나오니 너무나 당황스러웠다..
# 가장 중요한 건 가치
# [1]우선순위 큐 : 무게 고려하니 애매하다..
# [2]모든 경우의 수를 탐색
# -> 무게를 우선으로 일단 넣을 수 있는 경우를 다 탐색
# -> 그러고 우선순위 큐를 적용하면 어떨까?
# 6, 5, (3,4)
# 즉 3,4,5,6 을 조합해서 7이 안 넘게 하는 경우를 찾자.
import sys
input=sys.stdin.readline
n, k = map(int, input().split())
things = []
values = []
for i in range(n):
w, v = map(int,input().split())
things.append([w,v])
things.sort()
for i in range(n):
cur_k = things[i][0]
value = things[i][1]
for j in range(i+1, n):
if(cur_k + things[j][0] > k):
break
else :
cur_k += things[j][0]
value += things[j][1]
values.append(value)
values.sort()
print(values[-1])[G3][7579] 앱
[G5][15486] 퇴사 2
📌시도 1 : 시간 초과
문제를 풀면서 [G5][12865] 평범한 배낭과 유사하다고 생각되는 문제였다. 그래서 틀도 거의 비슷하게 가져가면서 논리에 맞게 수정하는정도로 문제를 풀었고 예제들을 넣었을 때 모두 정답이 나왔고 제출을 했지만 시간 초과가 떴다.
import sys
input=sys.stdin.readline
n = int(input())
schedual = []
profits = []
for i in range(n):
t, p = map(int,input().split())
schedual.append([t,p])
for i in range(n):
if(i + schedual[i][0] > n):
continue
profit = schedual[i][1]
i = i + (schedual[i][0])
for j in range(i, n):
if(i + schedual[j][0] > n):
continue
else :
i += schedual[j][0]
profit += schedual[j][1]
profits.append(profit)
profits.sort()
print(profits[-1])
