[백준:1753 최단경로][JAVA]

문제

방향그래프가 주어지면 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구하는 프로그램을 작성하시오. 단, 모든 간선의 가중치는 10 이하의 자연수이다.

<다익스트라를 구현하라는 문제다. 가중치, 방향이 존재 -> 다익스트라!>

다익스트라 개념

다익스트라 알고리즘을 공부하고 java로 구현해보는 시간이라고 생각했다.

우선 다익스트라의 개념부터 알아보자.
큰 흐름은
1. 현재 진행하는 단계에서 가장 가까운 거리를 선택한다
2. 그 거리가 기록되있는 거리보다 좋을 경우 갱신

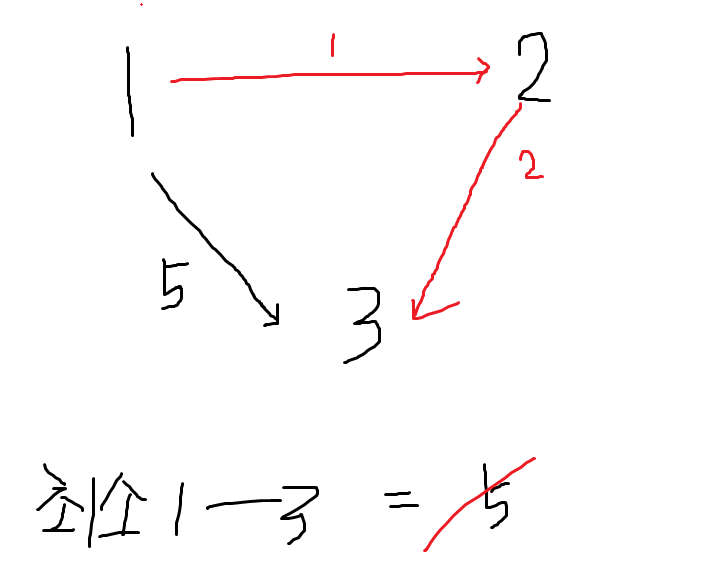
간단한 그림으로 보면 1->3으로 바로 가는 게 5가 걸리고
1->2->3 이 총 3이 걸린다면 결론은 1-2-3이 더 짧은 거리다!
이러한 행동을 반복하는 것이다!

💡 필요한 지식

우선순위 큐

우선순위 큐를 이용하는 이유는 반복문 속에서 현재 가장 작은 가중치를 구하는 것보다 우선순위 큐를 이용해서 짧은 거리 순으로 정리해두는 편이 더욱 효율적이기 때문이다!

[1] 선언

PriorityQueue<Node> que = new PriorityQueue();

[2] 우선순위 큐 사용을 위한 compareTo

public static class Node implements Comparable<Node>{
        int endNode = 0;
        int weight = 0;

		//생성자
        public Node(int a, int b){
            this.endNode = a;
            this.weight = b;
        }

		//우선순위 큐를 위해 미리..
        @Override
        public int compareTo(Node compNode){
            return this.weight - compNode.weight;
        }
}

우선순위 큐를 위해서는 comparable을 implements하고 그 클래스 안에서 compareTo를 오버라이드 해주어야한다!
우리는 우선순위 큐의 기준을 가중치로 둘 것임으로 위와 같이 만들어둔다!

[3] 흐름
우선순위 큐가 돌아가도록 첫 단계를 삽입해주어야한다.
처음 시작할 때는 시작 노드에서 갈 수 있는 노드들을 탐색한다!

que.add(new Node(startNode,0));
dist[startNode] = 0;

이렇게 시작 노드 -> 시작 노드로 가는 임의의 노드를 넣어주고 시작!

코드

import java.io.*;
import java.util.*;

public class Main {
    public static class Node implements Comparable<Node>{
        int endNode = 0;
        int weight = 0;

        public Node(int a, int b){
            this.endNode = a;
            this.weight = b;
        }

        @Override
        public int compareTo(Node compNode){
            return this.weight - compNode.weight;
        }
    }

    static int node;
    static int line;
    static List<Node>[] graph;
    static int[] dist;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        node = Integer.parseInt(st.nextToken());
        line = Integer.parseInt(st.nextToken());
        graph = new ArrayList[node+1];
        dist = new int[node+1];
        int startNode = Integer.parseInt(br.readLine());
        Arrays.fill(dist, Integer.MAX_VALUE);

        for(int i = 1; i <= node; i++){
            graph[i] = new ArrayList<>();
        }

        for(int i = 0 ; i < line; i++){
            st = new StringTokenizer(br.readLine());
            int u = Integer.parseInt(st.nextToken());
            int v = Integer.parseInt(st.nextToken());
            int w = Integer.parseInt(st.nextToken());

            graph[u].add(new Node(v,w));
        }

        leastDist(startNode);

        for(int i = 1 ; i < node+1; i++){
            int p = dist[i];
            if(p == Integer.MAX_VALUE)
                System.out.println("INF");
            else
                System.out.println(p);
        }
    }

    private static void leastDist(int startNode) {
        PriorityQueue<Node> que = new PriorityQueue();
        int[] visited = new int[node+1];
        que.add(new Node(startNode,0));
        dist[startNode] = 0;

        while(!que.isEmpty()){
            Node pollNode = que.poll();
            int cur = pollNode.endNode;

            if(visited[cur] == 1) continue;
            else visited[cur] = 1;

            for(Node curNode : graph[cur]){
                if(dist[curNode.endNode] > dist[cur] + curNode.weight){
                    dist[curNode.endNode] = dist[cur] + curNode.weight;
                    que.add(new Node(curNode.endNode, dist[curNode.endNode]));
                }
            }
        }
    }
}