📝최단경로의 개념
최단 경로 알고리즘 중 대표적인 알고리즘은 다익스트라 알고리즘이다.
다익스트라는 여러 노드들이 존재하는 그래프에서 출발노드부터 시작해서 다른 모든 노드를까지의 각 최단 경로를 구해줄 수 있다.
- 음의 간선이 없어야한다!
- 그리디, DP로 분류되기도 한다.
최단경로 단계
- 출발 노드를 설정한다.
- 최단 거리 테이블을 만들고 초기화한다.
2-1. 이 때 최단거리를 모두 무한으로 초기화! - 방문하지 않은 노드들 중 최단 거리가 가장 짧은 노드를 선택한다.
- 선택한 노드를 거쳐 다른 노드로 가는 비용을 계싼하여 거리 테이블을 업데이트한다.
3~4 반복
🤷♂️최단경로은 어디에 사용될까?
- 네이버 길 찾기
- 지하철 어플
- 자동차 네비게이션
문제풀이
[G3]1238] 파티
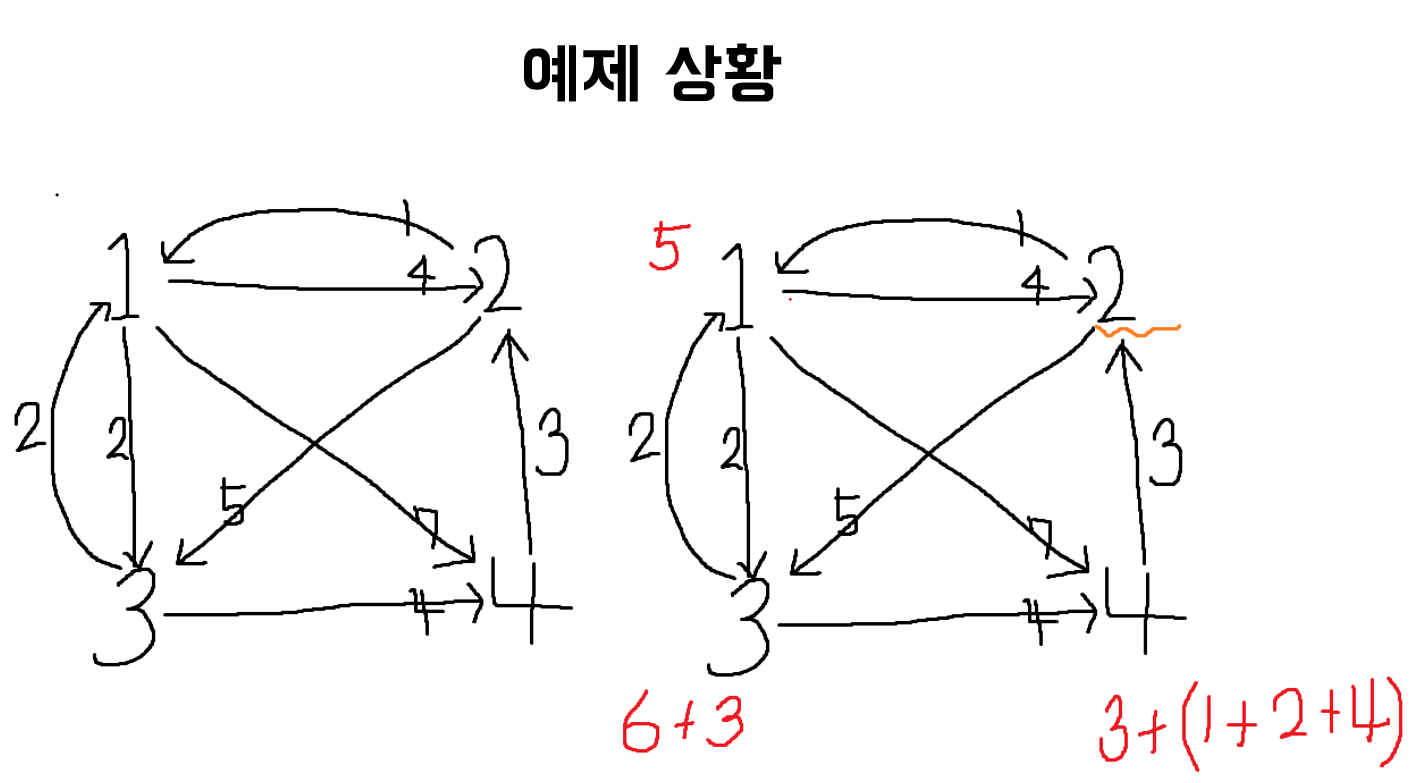
일반적인 다익스트라 알고리즘을 보면서 문제 자체에 적용하는 것에 어려움을 느꼈다. 다익스트라가 시작 지점부터 연결되있는 것들을 보고 그 중 최소 비용 골라서 다시 진행하는 걸 반복하는데 논리흐름만 안 상태에서 적용하기가 조금 곤란하게 느껴졌다. 그림도 그려보면서 어느 정도 처음에 많은 고민을 했다.
#def dijkstra(start,end):
# queue = 1
# q팝 -> 연결된거
# queue= 2,3,4
# 학생 : N명
# 단방향 도로 : M개
# 소요시간 : T
cnt_stu, cnt_road, placeParty = map(int,input().split())
# 그래프 정보 받기 : 딕셔너리로? 배열로?
# 중요 : 단순 연결정보뿐만 아니라 가중치까지 저장해야함
graph = [[] for _ in range(cnt_stu+1) ]
for _ in range(cnt_road):
start, end, cost = map(int, input().split())
graph[start].append((end, cost))
cnt = 0
for i in graph:
print(cnt, ":", i)
cnt+=1
# 다익스트라를 사람 수만큼 진행시켜야한다 -> 각 사람별 최소 왕복 거리 구하고 그 중 최대
# 최소경로 다 구해도 4->2->1->3->4 같은 경로를 어떻게 알 것인가..
# => 사람별 다익 두 번씩 : 출발할때 다익 한 번, 돌아올 때 다익 한 번
# costList = []
# for idx in range(1, cnt_stu+1):
# goCost = dijkstra(idx, placeParty)
# backCost = dijkstra(placeParty, idx)
# costList.append(goCost+backCost)
import heapq
import sys
input = sys.stdin.readline
def dijkstra(start):
# 연관된 부분 다 끄집어 내서 비용 계산
q = []
disLeast = [1e9 for i in range(cnt_stu + 1)]# 최소 경로 비용 저장하는 배열
heapq.heappush(q, (0, start)) # 큐에 시작 정보(시작지점이니 비용 0과 지점) 입력
disLeast[start] = 0
while(q):
# 기록된 거리와 장소 끄집어내기
dist, loc = heapq.heappop(q)
for go,cost in graph[loc]:
allCost = dist + cost
if(allCost < disLeast[go]):
disLeast[go] = allCost
if(go == start) : continue
heapq.heappush(q, (allCost, go))
return disLeast
cnt_stu, cnt_road, placeParty = map(int,input().split())
graph = [[] for _ in range(cnt_stu+1) ]
for _ in range(cnt_road):
start, end, cost = map(int, input().split())
graph[start].append((end, cost))
lastValue = 0
for curLocation in range(1, cnt_stu+1):
goCost = dijkstra(curLocation)
backCost = dijkstra(placeParty)
# 반환받은 최소 경로 비용 배열을 합산해 왕복 비용을 계산
lastValue = max(lastValue, goCost[placeParty] + backCost[curLocation])
print(lastValue)문제를 푸는 흐름 자체는 다익스트라의 정통 방식은 이었는데 머리 속에 계속 정리가 안된 게 계속 이동을 하는데 어떻게 최단 비용을 저장할지였다. 해결방안은 (비용, 시작점)을 큐에 넣고 큐를 반복해서 진행을 한다. 이때 시작에 연결되어있는 녀석들의 (비용, 시작노드)를 우선순위 큐에 넣기 시작한다. 그 후 넣은 큐가 소진될 때까지 진행하는데 큐에 넣는 과정 속에서 그래프 자체가 양방향 연결 그래프이기 때문에 만약 원래대로 돌아오는거라면 그냥 큐에 넣지도 않도록한다. 정상적 흐름이면서 거기다 최소 비용을 새로 갱신 시켜줄 수 있는 녀석이라면 가능성이 있으니 다시 큐에 넣으면된다.
여기가 가장 생각하기 어려웠는데
(1) 이 전에 넣어둔큐에서 꺼내서 (거리, 지역)을 저장해둔다.
(2) 반복문 : 지역에서 갈 수 있는 도로들의 정보를 꺼내온다.
(3) (1)에서 꺼내둔 거리 + 갈 수 있는 도로 비용 < 최소 비용 배열 => 만족 시 수정 후 큐에 넣는다.
(1)에서 꺼내둔 거리를 이용해서 계속 다른 도로로 이동하지만 비용을 더해가면서 움직일 수 있는 것이다!!!
[G4]4485] 녹색 옷 입은 애가 젤다지?
#BFS로 풀어볼까? => 지나간 흔적 남기기가 조금 애매한데?
# 1 3
# 2 7
# -> 1 3 7이 먼저 되서 11되버리면 어쩔래?
# -> visited를 없애고 모든 칸에서 다 계산해볼까..처음 이 문제를 보고 BFS나 DFS로 문제를 풀어볼까 하는 생각이 들었다.
뭔가 시작 위치에서부터 상하좌우로 이동하면서 적당히 이동한 경로만 잘 적어놓는다면 되지 않을까 싶었는데 생각을 하다보니 BFS는 방문여부를 체크하면서 무한루프에 빠지는 일이 없는데 이러한 곳에서는 오히려 멀리 돌아가더라도 그게 최단경로가 될 수도 있고 동시에 위에 내가 적어둔 것처럼 1->3->7 보다 1:2:7이 가까울 수도 있는데 이런 경우 visited를 사용할 수 없을 것 같아서 다익스트라 알고리즘을 풀려고 다익스트라 개념을 다시 보러 이동 중 해당 문제를 BFS로도 해결하신 분을 보았다. 어떻게 BFS개념을 이용해서 풀 수 있을까 하는 생각을 했는데 애초에 경로를 이동하면서 기록중에 최소가 되는 경우에만 append를 하고 아닌 경우에는 append를 아예 안하고 visited 자체도 사용하지 않는 것이다. 솔직히 서칭을 하다 우연히 발견하지 못했다면 BFS로는 못 풀었을 것 같았다. 많이 연습한 BFS지만 문제에 잘 적용하지 못했다. 더 연습해야겠다. 또한 다익스트라로도 해당 문제를 풀어보아야겠다.
import sys
from collections import deque
input = sys.stdin.readline
def BFS(cave, minMove):
queue = deque()
queue.append((0,0))
dx = [1,-1,0,0]
dy = [0,0,1,-1]
while(queue):
cX,cY = queue.popleft()
for idx in range(4):
moveX = dx[idx] + cX
moveY = dy[idx] + cY
# 허용 범위 내
if((0 <= moveX < cave_size) and (0 <= moveY < cave_size)):
# 지금 값이 더 괜찮으면 넣고 다시 큐에 넣기
if(minMove[moveX][moveY] > minMove[cX][cY] + cave[moveX][moveY]):
minMove[moveX][moveY] = minMove[cX][cY] + cave[moveX][moveY]
queue.append((moveX,moveY))
cnt = 1
endValue = 0
while(True):
cave_size = int(input())
if(cave_size == endValue):break
cave = []
for i in range(cave_size):
cave.append(list(map(int, input().split())))
minMove = [[int(1e9) for i in range(cave_size)] for j in range(cave_size)]
minMove[0][0] = cave[0][0]
BFS(cave, minMove)
print(f'Problem {cnt}: {minMove[cave_size-1][cave_size-1]}')
cnt+=1
[G4]1504] 특정한 최단 경로
😥 시도 1 : 틀렸습니다(3%)
이 문제를 풀기 전에 미리 흐름을 생각해봤다.
# 단순 최소 경로가 아니라 꼭 들려야한다..
# 다익스트라(출발, 꼭 방문1) -> 다익스트라(출발, 꼭 방문2) -> 최종노드
# 다익스트라(출발, 꼭 방문2) -> 다익스트라(출발, 꼭 방문1) -> 최종노드꼭 들려야만 하는 경로가 2개니까 애초에 시작지점에서 꼭 방문해야하는 노드를 한 번 방문하고, 방문한 노드를 시작 노드로 두고 두 번째 방문해야하는 노드를 방문하는 최소 경로를 구하고 마지막으로 두번째 방문해야할 노드를 시작으로 끝점까지 움직인다.
해당 논리를 기반으로 코드를 만들었지만 틀렸다.
import sys
import heapq
input = sys.stdin.readline
def dijkstra(start):
q = []
costLeast = [10000000 for i in range(cntNode + 1)]# 최소비용 배열
costLeast[start] = 1
# 큐에 (비용,시작)
heapq.heappush(q, (start, 0))
# 연결된 거 다 빼자
while(q):
startNode, cost= heapq.heappop(q)
for targetNode, gocost in graph[startNode]:
allCost = cost + gocost
if(allCost < costLeast[targetNode]):
costLeast[targetNode] = allCost
heapq.heappush(q, (targetNode, allCost))
return costLeast
cntNode, cntLine = map(int,input().split())
graph = [[] for _ in range(cntNode + 1) ]
for _ in range(cntLine):
start, end, cost = map(int, input().split())
graph[start].append((end, cost))
mustGo1, mustGo2 = list(map(int,input().split()))
cost1 = dijkstra(1)
cost2 = dijkstra(mustGo1)
cost3 = dijkstra(mustGo2)
road1 = cost1[mustGo1] + cost2[mustGo2] + cost3[cntNode]
road2 = cost1[mustGo2] + cost3[mustGo1] + cost2[cntNode]
if(road1 >= 10000000 and road2 >= 10000000 ) : print(-1)
else:
if(road1 < road2) : print(road1)
elif(road1 > road2) : print(road2)😥 시도 2 : 틀렸습니다(60%)
생각하다보니 다시 간선으로 돌아올 수도 있다는 것을 포함 안해줬다..
for _ in range(cntLine):
start, end, cost = map(int, input().split())
graph[start].append((end, cost))
graph[end].append((start, cost))이렇게 왕복할 수 있도록 길을 만들어줬다. 다시 제출하니 60%까지 올라가더니 틀려버렸다..이젠 정말 뭐가 문제인지 잘 모르겠다. 문제에 다시 갔던 경로로 이동하는 거에 대한 비용 언급이 없긴한데 설마 다시 간 경로는 비용을 안 들이는걸까.
😥 시도 3 : 틀렸습니다(82%)
혹시나해서 임의로 10억을 넣은 숫자를 1e9로 변경하고, if문 논리를 조금 수정해주었다. 그러니 22% 오른 82%에서 틀렸다고 나왔다..하..뭐가 문제일까ㅠㅠ
import sys
import heapq
input = sys.stdin.readline
def dijkstra(start):
q = []
costLeast = [ 1e9 for i in range(cntNode + 1)]# 최소비용 배열
costLeast[start] = 1
# 큐에 (비용,시작)
heapq.heappush(q, (start, 0))
# 연결된 거 다 빼자
while(q):
startNode, cost= heapq.heappop(q)
for targetNode, gocost in graph[startNode]:
allCost = cost + gocost
if(allCost < costLeast[targetNode]):
costLeast[targetNode] = allCost
heapq.heappush(q, (targetNode, allCost))
return costLeast
cntNode, cntLine = map(int,input().split())
graph = [[] for _ in range(cntNode + 1) ]
for _ in range(cntLine):
start, end, cost = map(int, input().split())
graph[start].append((end, cost))
graph[end].append((start, cost))
mustGo1, mustGo2 = list(map(int,input().split()))
cost_start = dijkstra(1)
cost_mustgo1 = dijkstra(mustGo1)
cost_mustgo2 = dijkstra(mustGo2)
road1 = cost_start[mustGo1] + cost_mustgo1[mustGo2] + cost_mustgo2[cntNode]
road2 = cost_start[mustGo2] + cost_mustgo2[mustGo1] + cost_mustgo1[cntNode]
leastCost = min(road1, road2)
print(leastCost if leastCost < 1e9 else -1)😍 시도 4 : 맞았습니다
엄청 어이없게 해결했다.
그냥 코드를 다시 쭈욱 읽어보다 다익스트라의 시작 지점은 비용을 1로 설정해두었는데 그걸 비용을 0으로 하고 돌려보니 맞았다.. 당연하게도 자기 지점에서 시작하는데 시작지점에서 시작지점으로 이동하는데 비용이 1이라는 것 자체가 말이 되지 않는 것이었다. 아무튼 해결해서 기분이 좋다!
[G1]1162] 도로포장
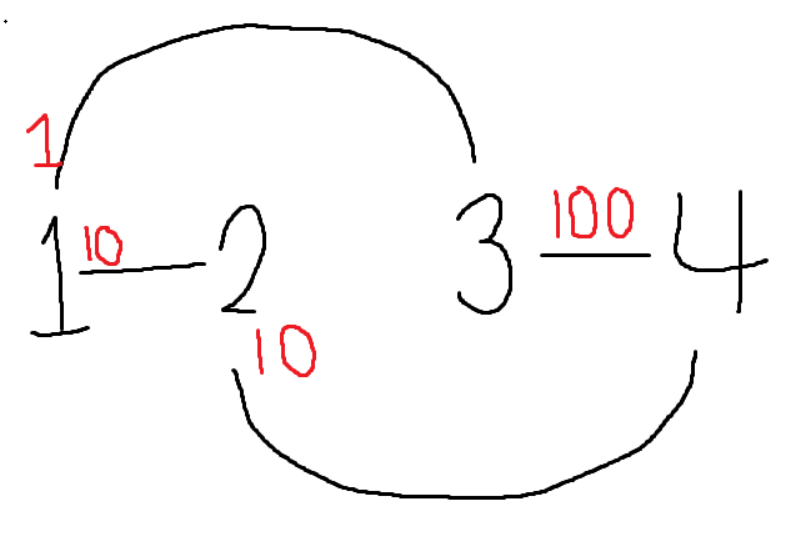
일반적인 다익스트라 문제에 존재하는 도로 중 주어지는 갯수만큼은 도로 이동 비용을 0으로 만들어 줄 수 있다는 것이 특별했다. 어떻게 논리 흐름을 잘 정하고 가느냐가 가장 중요한 것 같았다.

