🔍️DFS의 개념
DFS(Depth-First Search)는 그래프 탐색 기법
그래프란 정점(Vertex)와 정점을 연결하는 간선(edge)의 집합으로 이루어져있으며, 연결되어있는 정점들간의 관계를 표현한 것이다. 이러한 그래프에서 하나의 정점에서 시작하여 차례대로 모든 정점들을 하나씩 방문하는 방법 즉 탐색하는 방법 중 하나가 DFS이다.
🌱 DFS 예시
트리를 순회할 때 전위,후위,중위 3가지 순회 방식을 학습한 적이 있다.
이 3가지 순회방식이 모두 DFS이다. 자식 줄기들을 모두 타고 내려가고, 마지막까지 다 방문했다면 그 다음 줄기로 이동하고 반복하는 형식으로 진행한다.
🚧 DFS의 진행방식
DFS는 보통 Stack을 사용해서 구현한다.
- 스택을 생성
- 스택에 탐색을 시작할 노드를 넣는다
- 스택에 있는 노드를 꺼낸다
- 꺼낸 노드 : 방문 기록 남기기
- 꺼낸 노드 : 출력
- 꺼낸 노드 : 자식들을 스택에 담자
- 스택에 남아있는 게 없을 동안 : 3~7을 반복
💻 DFS의 코드를 보자
아래 그림과 같이 메뉴판이 있다고 할 때 코드로 DFS를 구현해보자
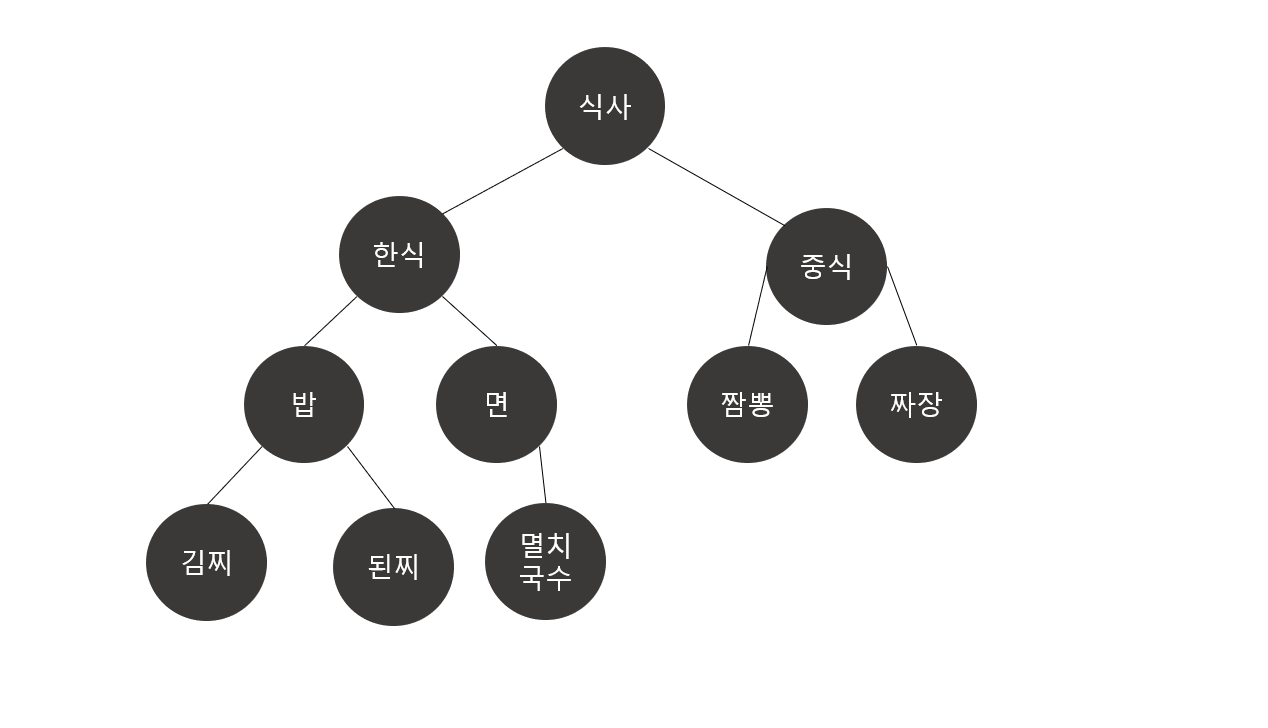
def dfs(graph, start):
visted = [] #이미 방문
stack = [start] # (1,2) 방문해야할 스택
cnt = 0
# 스택에 꺼낼 게 남아있는동안
while(stack):
node = stack.pop() # (3)pop
# 만약 꺼낸 게 아직 방문하지 않은거라면?
if (node not in visted):
cnt+=1
visted.append(node) # (4) 방문 기록 남기기
print(cnt , ':' , node) # (5) 꺼낸 노드 출력
stack.extend(graph[node]) # (6) 꺼낸 노드의 자식을 스택에 담자
# 그래프 생성
graph = dict()
graph['식사'] = ['한식', '중식']
graph['한식'] = ['식사','밥', '면']
graph['중식'] = ['식사','짬뽕', '짜장']
graph['밥'] = ['한식', '된찌', '김찌']
graph['면'] = ['한식','멸치국수']
graph['멸치국수'] = ['면']
graph['짬뽕'] =['중식']
graph['짜장'] =['중식']
graph['김찌'] =['밥']
graph['된찌'] =['밥']
dfs(graph, '식사')⚾ DFS : 재귀
DFS는 이렇게 스택을 활용하여 구현하는 것이 이해하기 쉽지만, 재귀함수를 이용하면 확실히 줄어든 코드 수로 함수를 수행하는 것이 가능하다. 주석을 많이 달아 두었기 때문에 코드가 길어 보이지만 앞선 코드에 비해 확실히 간결하다.
visted = []
def re_dfs(graph, cur):
visted.append(cur) #현재 노드를 방문했다고 체크해두자.
# 현재 노드의 자식들을 뽑자
# 밑에까지 다 탐색하고 다시 올라와서 다른쪽
for node in graph[cur]:
if node not in visted: # 방문하지 않은 노드라면?
print('현재: ', node)
re_dfs(graph, node)
# 그래프 생성
graph = dict()
graph['식사'] = ['한식', '중식']
graph['한식'] = ['식사','밥', '면']
graph['중식'] = ['식사','짬뽕', '짜장']
graph['밥'] = ['한식', '된찌', '김찌']
graph['면'] = ['한식','멸치국수']
graph['멸치국수'] = ['면']
graph['짬뽕'] =['중식']
graph['짜장'] =['중식']
graph['김찌'] =['밥']
graph['된찌'] =['밥']
re_dfs(graph, '식사')
print(visted)
# 방문 : 식사, 
