05_week_완전이진트리

이 이론의 목표는 RB tree를 구현하는 것이다

linked list 를 지나서 완전이진트리에 진입을 하였다.
완전이진트리는 이진트리의 한 종류로 모든 노드들이 꽉 차있지는 않지만 중간에 빈 곳이 없이 채워져있는 것을 얘기한다 (모든 노드가 가득 차있는건 포화 이진 트리)

아래 그림과 같이 노드가 연결되는 구간 (마지막 레벨을 제외한 모든 곳)에 빈곳이 없이 차있는 것을 확인할 수 있다 (노드도 순서대로 차있어야함)

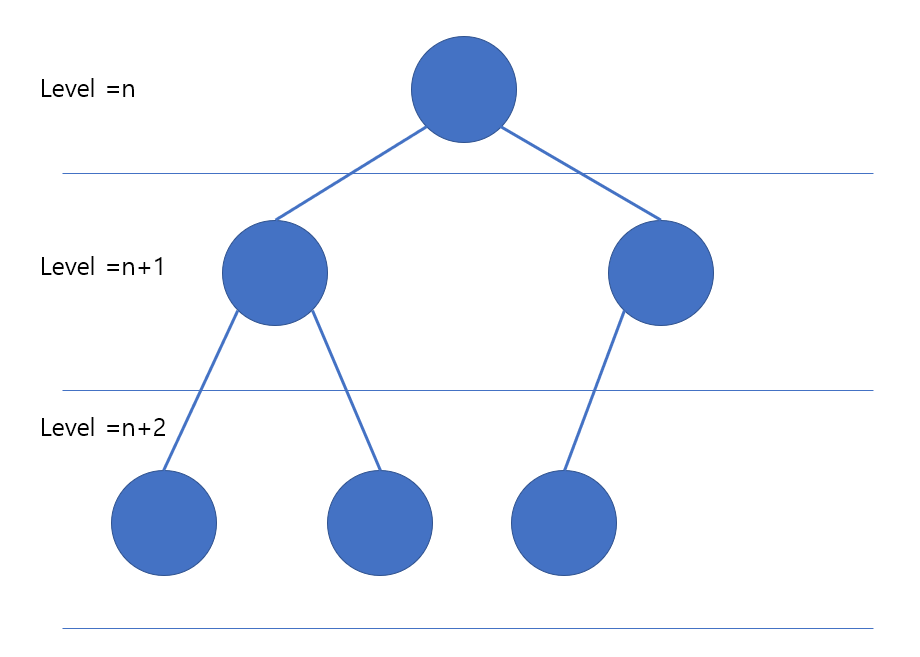
아래와 같은 탐색 트리는 완전이진탐색트리가 아님
마지막 level을 제외하고 모든 level이 차 있지만 마지막 level에서 노드가 순서대로 차있지 않기 때문임

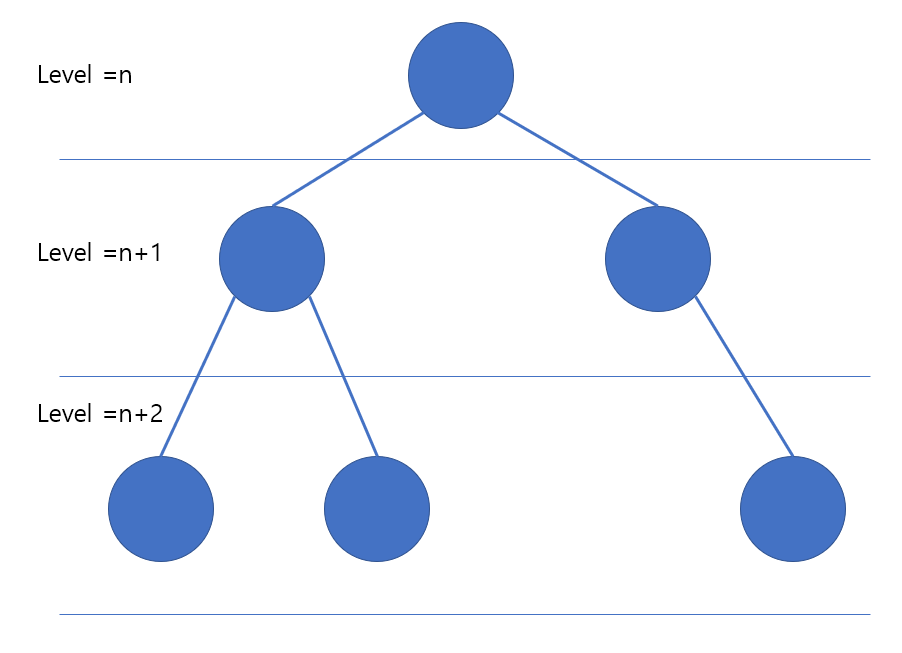
이진 트리의 표현 방법은 2가지

1. 배열 표현
2. 포인터 표현

1. 배열 표현
완전이진 트리는 주로 배열 표현을 사용함
저장하고자 하는 이진 트리를 완전 이진트리라고 가정
이진 트리의 깊이가 $2^k-1$ 개의 공간을 연속적으로 할당한 다음, 완전 이진 트리의 번호대로 노드를 저장

부모의 번호2= 왼쪽 자식의 번호
부모의 번호2+1 = 오른쪽 자식의 번호

리스트 사용시 0번은 비우고 1번부터 채우는 것을 추천
0번을 사요하게 되면 루트가 0번이 되고 위 공식들이 성립하지 않음

2. 포인터 표현
트리의 노드가 구조체로 표현되고, 각 노드가 포인터를 가지고 있어서 이 포인터를 이용하여 노드와 노드를 연결하는 방법

ref 완전이진트리