Librarian Sort오늘 공부한 내용 ⛅
오늘은 자료구조 중 힙, 트리, 트라이와 알고리즘 중 정렬, 이진 탐색에 대한 내용을 배웠다.
트라이는 처음 배우는 것 같아서 쓸 내용이 많을 것 같다.
새로 알게된 내용 🌱
트라이
Retrieval tree 에서 이름이 유래했고 문자열을 탐색하는 용도로 대부분 사용된다.
문자열의 길이를 L이라고 할 때 탐색과 삽입은 O(L) 시간이 요구된다.
문자열을 단순 비교하여 탐색하는 것보다 효율적이지만 각 노드가 자식에 대한 링크를 모두 갖고있어야 하므로 메모리를 많이 사용한다.
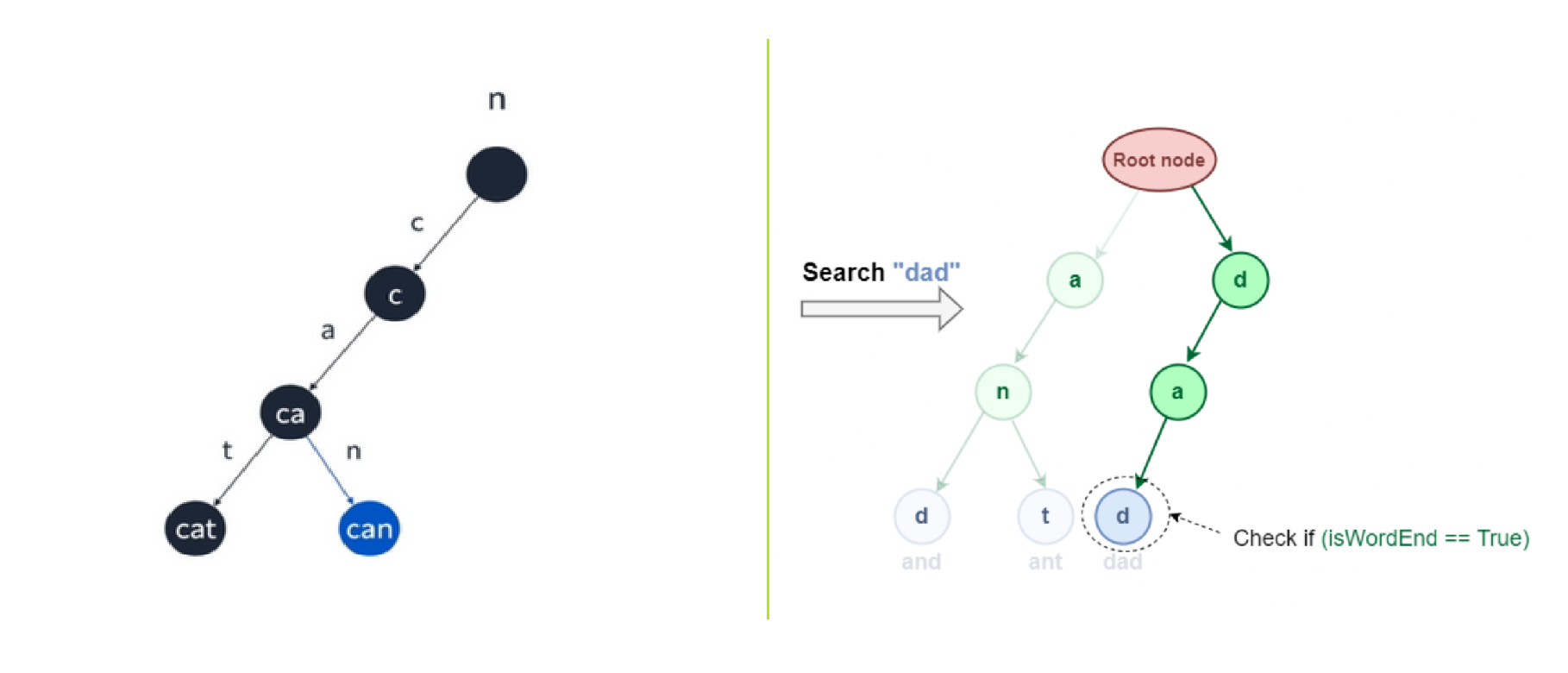
루트는 비어있는 상태를 유지하고 간선은 가능한 문자 값을 키로 가지며 간선으로 이어진 노드는 부모 노드의 값에 간선의 키를 이은 값을 가진다.
또는 단어의 종료 지점을 식별하는 flag를 만들어 단어의 종료 시점에만 단어 데이터를 저장하는 방식도 있다.
보통의 경우에는 해시 테이블보다 느리지만 worst case에서는 빠를 수 있다.
데이터를 추가, 삭제하는 기능이 있으므로 사전이나 전화번호부 등을 구현하는데 사용될 수도 있고 맞춤법 검사를 구현하는데 사용될 수도 있다.
처음 배우는 것 같은데 학교에선 스킵한 걸까 내가 까먹은 걸까..
Parametric Search
주어진 문제를 결정문제로 변형하여 이분탐색을 통해 해결하는 방법을 말한다.
어떤 값을 찾는 문제를 지금 값이 조건을 만족하냐/아니냐로 바꾸어 값을 점진적으로 찾아나가는 문제로 바꿀 수 있을 때 사용할 수 있다.
적용 가능 조건은 다음과 같다.
- 최댓값이나 최솟값을 구하는 문제
- 조건 검사 결과가 변하는 지점이 하나
- 답의 범위가 이산적이거나 허용 오차 범위가 존재
처음에 임의로 크게 잡은 범위를 M, 조건 함수가 수행되는 시간을 O(C(n)) 이라하면 총 시간 복잡도는 O(C(n) log M) 이다.
적용하려고 할 때 필요한 게 논리적 사고와 전산화 능력인 것 같다.
리마인드된 내용 🔨
O(n^2) 정렬 알고리즘
버블 정렬과 선택 정렬은 O(n^2) 의 시간 복잡도를 가지기에 머지 정렬이나 퀵 정렬보다 느리다.
그러면 두 정렬 방법이 실제로 쓰이는 곳이 있기는 하는 지가 궁금했다.
답은 요소가 대략 10개 미만인 경우에는 다른 정렬보다 빠르다고 한다.
물론 10log10 과 10^2 를 비교하면 전자가 더 작으니 이상하게 느껴질 수 있지만 분산식 정렬은 쪼개고 다시 합치는 overhead가 존재하므로 실제 실행 결과에서 차이가 나타난다.
개수가 작으면 시간 차이가 미미하니 의미가 있나 싶기도 하다.
그러나 분할 정복 방법을 쓰면서 부분의 크기가 작아진 경우에 분할 정복을 대체해서 사용한다면 여러 번 사용되기 때문에 제법 유의미한 효과를 볼 수 있다.
O(n^2) 정렬 중에서도 보통 선택 정렬이 효율적이라고 한다.
삼천포 ⚓
Tim Sort
위 정렬 관련된 내용을 작성하면서 자바스크립트의 Array.sort() 는 어떤 구현 방식을 선택했을 지 궁금했다.
ECMAScript 자체에서 방식을 지정하지는 않았고 v8 엔진의 경우 Tim Sort 로 구현했다고 한다.
이건 또 뭘까 싶었지만 간단히 요약하면 머지 정렬과 선택 정렬을 결합한 뒤 최적화를 한 방식이다.
정렬 알고리즘을 실제 적용할 때 고려하는 것은 시간복잡도만은 아니다.
요즘은 가용 용량이 많이 늘어났지만 메모리도 중요 요소이다.
또한 CPU가 데이터를 가져올 때는 참조 지역성의 원리에 따라 사용할 것으로 예측되는 데이터도 캐시로 같이 가져오므로 해당 측면에서 얼마나 유리한가도 따져봐야 한다.
이론적으로는 힙 정렬이 이상적이어 보이지만 참조 지역성이 좋지 않다.
퀵 정렬은 worst case가 치명적이다.
머지 정렬은 참조 지역성은 좋지만 메모리를 요소 개수만큼 사용해야 한다.
삽입 정렬은 시간복잡도는 크지만 인접한 요소에 대한 비교가 빈번하게 이루어지기에 참조 지역성의 원리를 가장 잘 만족한다.
또한 메모리도 적게 사용한다.
Tim 정렬은 이중 머지 정렬과 삽입 정렬을 사용하여 각각의 단점을 보완하는 방식을 취한다.
먼저 데이터를 2^x개로 나누어 각각을 삽입 정렬로 정렬한다. 각 나눠진 집합은 run 이라고 한다.
x는 가장 효율적으로 정렬을 수행할 수 있도록 내부적으로 설정한다.
더불어 머지 정렬의 병합 횟수를 최대한 줄이기 위해 run 인접 요소가 해당 run의 정렬 순서에 부합한다면 인접 요소도 run에 포함시킨다.
랜덤한 데이터가 아닌 실사용 데이터의 경우 부분적으로 방향성을 가지는 구간이 나타나는데 위 방법을 통해 해당 구간을 하나로 묶을 수 있다.
위에서 적은 내용과는 다르게 쪼개기 전에 덩어리를 만든다.
삽입 정렬은 일반적인 삽입 정렬 대신 이분 삽입 정렬을 사용하여 참조 지역성을 약간 손해보는 대신 삽입 위치 찾는 과정을 빠르게 한다.
머지 정렬에서도 최적화 기법이 들어간다.
먼저 run을 stack에 push하면서 크기 규칙을 만족하도록 병합을 한다.
이 과정을 통해 비슷한 크기의 run 끼리 병합을 시킬 수 있으며 stack의 크기도 작게 유지할 수 있다.
또한 메모리를 적게 사용하기 위한 최적화 기법도 이루어진다.
이를 통해 실생활에서 사용되는 일정 패턴이 존재하는 데이터에서 빠른 성능과 안정성을 가지고 최악의 경우에도 O(n log n) 시간 복잡도를 가진다.
덕분에 많은 언어에서 표준 정렬 알고리즘으로 사용되고 있다.
생각해보면 북카트를 끌고 서가를 정리할 때도 카트의 칸마다 적당히 분리하면서 삽입 정렬을 하고 마지막에 책장에 병합했던 것 같다.
느낀점 🎬
실습 문제를 풀면서 sort를 맘대로 써도 시간이 문제되지는 않을까 하면서 내심 의심을 가진 적이 꽤 있었는데 깊게 알아보니 신뢰가 생겨났다. 생각해보면 왜 의심을 가졌을까 싶기도한데 자바스크립트에 대한 불신을 내가 갖고 있던걸까.
그나저나 Tim sort 도 왠지 알고리즘 수업에서 소개가 되었을 것 같은데 머릿속에 존재하지 않는다.
과거의 나는 도대체..

