배낭 문제란 무엇인가?

예시로 그림을 보면서 이해해보자

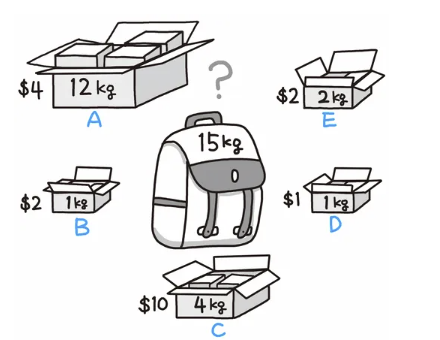
지금 현재 나는 15kg 용량까지 넣을 수 있는 배낭을 가지고 있다.
그리고 주변에는 여러가지 물건들이 있는데
그 물건들은 각각 무게와 가치를 가지고 있다.

배낭의 최대 용량을 넘지 않는 선에서
어떤 물건들을 넣어야 최대 가치를 얻을 수 있을까?
예를 들어 , 이 그림에서는 A,E,D 물건을 넣어야
배낭의 최대 용량 15kg을 넘지 않으면서 최대 가치인 $7를 얻을 수 있다.

즉, 물건들을 잘 조합해서 배낭의 최대 용량을 초과하지 않으면서
담은 가치를 최대로 하는 문제가 배낭 문제이다.

배낭 문제를 어떻게 풀어야 할까??🤔

배낭 문제는 물건을 쪼갤수 있냐 없냐에 따라 풀이법이 달라진다.

물건을 쪼갤수 있다!
⮕ 부분 배낭 문제 ( fractional knapsack problem )

물건을 쪼갤수 없다!
⮕ 0/1 배낭 문제 ( 0/1 knapsack problem )

부분 배낭 문제 ( fractional knapsack problem )

해결 방법 :
무게당 가치가 높은 짐을 최대한 많이 넣는 그리디 알고리즘을 사용한다.

예시 )

𝐀 ⮕ 무게당 가치 : $4 ÷ 12kg = 1/3
𝐁 ⮕ 무게당 가치 : $2 ÷ 1kg = 2
𝐂 ⮕ 무게당 가치 : $10 ÷ 4kg = 2.5
𝐃 ⮕ 무게당 가치 : $1 ÷ 1kg = 1
𝐄 ⮕ 무게당 가치 : $2 ÷ 2kg = 1

무게당 가치
C > B > D=E > A

부분 배낭 문제 풀이

1. 무게당 가치가 제일 높은 C를 다 넣는다.
   ⮕ 배낭 용량 15kg-> ( 15kg - 4kg )=11kg
   ⮕ 이 때의 최대 가치 : $10

2. 무게당 가치가 그 다음으로 높은 B를 넣는다.
   ⮕ 배낭 용량 11kg -> ( 11kg - 1kg ) = 10kg
   ⮕ 이 때의 최대 가치 : $10+ $2 = $12

3. 무게당 가치가 그 다음으로 높은 D,E를 넣는다.
   ⮕ 배낭 용량 10kg -> ( 10kg - (1+2)kg ) = 7kg
   ⮕ 이 때의 최대 가치 : $12+ $1 +$2 = $15

4. A를 쪼개서 7kg를 마저 채운다.
   ⮕ 배낭 용량 7kg -> ( 7kg-7kg ) = 0kg
   ⮕ 이 때의 최대 가치 : $10 + $2 + $1 +$2 + $( 1/3 * 7 ) = 약 $17.3

위 과정이 끝나면
최대 가치는
$10 + $2 + $1 +$2 + $( 1/3 * 7 ) = $17.3 이 된다.

즉 , 요약하자면
1. 물건별로 무게당 가치를 구한다.
2. 무게당 가치가 높은 물건부터 넣을 수 있는 만큼 배낭에 넣는다.
( 만약에 배낭 용량이 물건 무게보다 작으면 물건을 쪼개서 넣는다. )
3. 배낭이 허용하는 용량이 0이 될때까지 과정2를 수행한다.

이렇게 그리디 알고리즘으로 부분 배낭 문제를 풀수 있다.

그렇다면 물건을 쪼갤수 없는
0/1 배낭 문제는 어떻게 풀어야 할까?

대표적인 0/1 배낭 문제

https://www.acmicpc.net/problem/12865

이 문제는 물건을 쪼갤수 없는 대표적인 0/1 배낭 문제이다.
어떻게 풀어야 할까?🤔

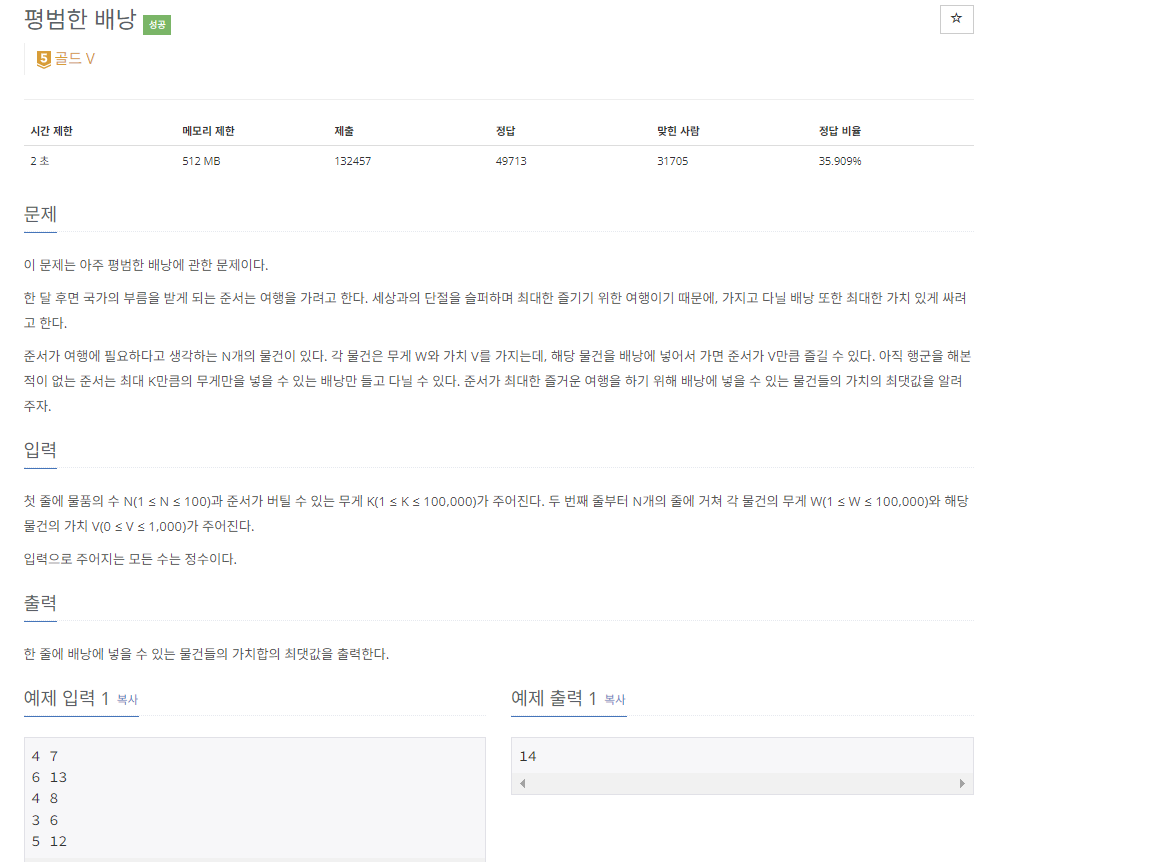
문제 요약

준서는 K 용량의 배낭을 가지고 있다.
그리고 준서는 N개의 물건을 가지고 있는데
각각의 물건은 무게 W , 가치 V를 가지고 있다.
배낭에 넣을 수 있는 물건들의 가치합의 최댓값을 구해야 한다.

문제 풀이

평범한 배낭 예제 입력 1을 바탕으로 풀어보겠다.
예제 입력 1에서는
배낭의 총 용량을 7kg , 물건의 수를 4로 입력하였다.
또한 각각의 물건들에 대한 무게와 가치를 입력하였다.
편의상 물건들에 대한 이름을 붙였다.

예를 들어
A 물건은 6kg 용량과 가치 $13을 가지고 있다.
B 물건은 4kg 용량과 가치 $8을 가지고 있다.
C 물건은 3kg 용량과 가치 $6을 가지고 있다.
D 물건은 5kg 용량과 가치 $12을 가지고 있다.

준서는 이제 배낭을 싸려고 한다.
준서는 물건을 쪼개서 넣을수 없으므로
준서는 배낭에 각각의 물건에 대해
물건을 넣지 않는다 or 물건을 넣는다.
이 두가지 행동만을 할수 있다.
즉 , 0/1 배낭 문제이다.

2차원 배열을 세워서 풀어보자!!

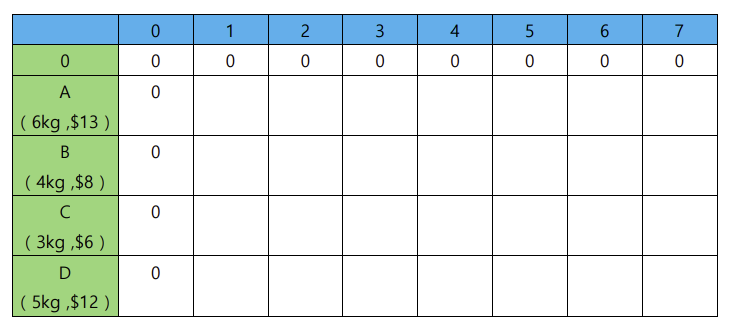
초기 배낭

파란색 줄은 배낭의 최대용량을 뜻하고
초록색 줄은 물건들을 뜻한다.
배열의 각 칸은 배낭의 최대 용량에 따른 최대가치이다.

배낭에 아무것도 넣지 않으면 최대 가치는 0이므로 0으로 채워준다.
더해서
배낭의 최대 용량이 0이라면 아무것도 넣을수 없으므로
최대 가치는 0이다 >> 0으로 채워준다.

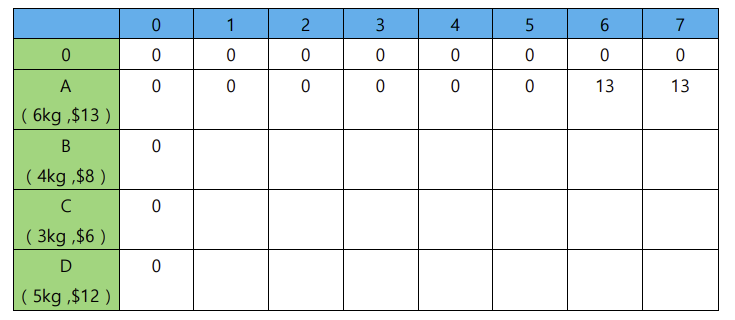
A를 배낭에 넣어보자

A는 무게가 6kg이므로 배낭의 최대 용량이
배낭의 최대 용량이 0~5kg 일때는 넣지 못한다.
배낭의 최대 용량이 6,7kg 일때 A를 넣을 수 있으므로
배낭의 최대 용량이 6,7kg 일때의 최대 가치는
A가 들어있는 경우인 $13이다.

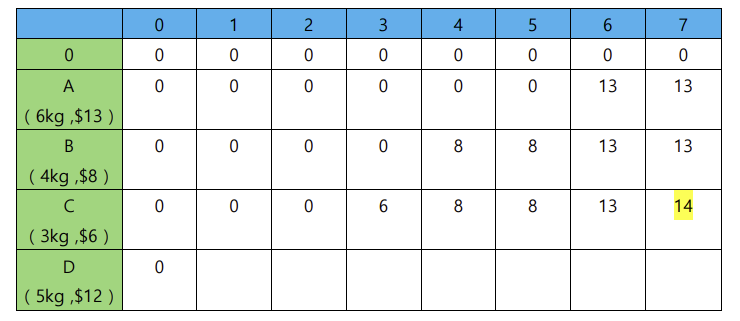
B를 배낭에 넣어보자

B는 무게가 4kg이므로
배낭의 최대 용량이 0~3kg 일때는 넣지 못한다.
배낭의 최대 용량이 4,5,6,7kg 일때 B를 넣을수 있다.
하지만 여기서 생각해볼 것이
A가 현재 배낭에 들어있는 경우와 들어있지 않은 경우를 생각해봐야한다.
A가 들어있는 경우 남은 배낭 용량은 1kg이므로 B를 넣지 못한다.
따라서
A만 들어있는 경우 vs A를 빼고 B를 넣는 경우로 최대 가치가 정해진다.

C를 배낭에 넣어보자

C는 무게가 3kg이므로 배낭의 최대 용량이 0~2kg 일때는 넣지 못한다.
배낭이 수용할수 있는 용량이 3,4,5,6,7kg 일때 C를 넣을 수 있다.
여기서 형광펜으로 칠해진 곳을 보자 어떻게 14가 나왔을까??
준서는 두가지 행동을 할수 있다고 하였다.
물건을 넣는다 or 물건을 넣지 않는다
두가지 행동 중 선택할수 있다.

만약에 준서가 C를 넣지 않는다면
배낭의 최대용량이 7일때의 최대 가치인 13이 그대로 내려온다.

만약에 준서가 C를 넣는다면
배낭의 최대 용량이 7일때에 최대가치는
C의 가치 + [ 배낭의 최대 용량이 ( 7-C의 무게 ) ]일때의 최대가치를
더해준 값이다.
즉
C의 가치 -> $6 ,
[ 배낭의 최대 용량이 ( 7-C의 무게 ) ] -> $8를 더한 값인 14가 된다.
당연히 14가 13보다 크므로
배낭의 최대 용량이 7일때의 최대가치는 14가 된다.

여기서 점화식을 얻을 수 있는데

배낭의 최대용량이 넣으려는 물건보다 작을때
⮕ 물건을 넣으면 안된다.
즉 , 물건을 넣기전 배낭 상태의 최대가치가 그대로 최대가치가 된다.
⮕ dp[i][j]=dp[i-1][j] 이란 점화식이 나온다.

배낭의 최대용량이 넣으려는 물건보다 클때
⮕ 물건을 넣지 않는다 or 물건을 넣는다.
물건을 넣지 않는다 ⮕ dp[i][j]=dp[i-1][j]
물건을 넣는다 ⮕ dp[i][j]=dp[i-1][j-weight]+value
여기서 value를 더해주는 것이 물건을 넣어주는 행위이다.
이 두개를 비교해서
더 큰 값을 집어넣는다.

마지막으로 D를 넣어보자

위에 나온 점화식을 바탕으로 2차원 배열의 칸들을 채워보면
모든 경우의 수를 따졌을때의
최대 가치는 14가 나온다는 것을 알수 있다.

이것을 코드로 짜면..(Feat.자바)

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;

class Main{

    static int N,K; // N -> 물건의 갯수 , K -> 배낭의 최대 용량
    static int [][]dp; // 다이내믹 프로그래밍 2차원 배열
    static ArrayList<int[]>bag_list; // 물건 리스트

    public static void main(String []args)throws IOException {
        
        BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st=new StringTokenizer(br.readLine());

        N=Integer.parseInt(st.nextToken()); // 물건의 갯수 입력 받기
        K=Integer.parseInt(st.nextToken()); // 배낭의 최대용량 입력 받기
        dp=new int[N+1][K+1]; // 2차원 배열 생성
        bag_list=new ArrayList<>(); // 물건 리스트
        bag_list.add(new int[]{0,0}); // 나중에 더 for문 편하게 돌리기 위해서 넣음.
        
        for(int i=0;i<N;i++) // 물건들 입력받기
        {
            st=new StringTokenizer(br.readLine());
            int weight=Integer.parseInt(st.nextToken()); // 무게 입력받기
            int value=Integer.parseInt(st.nextToken()); // 가치 입력받기
            bag_list.add(new int[]{weight,value}); // 물건 리스트에 넣어주기
        }

        for(int i=1;i<bag_list.size();i++) // 물건들 갯수만큼
        {
            int weight=bag_list.get(i)[0]; // 무게
            int value=bag_list.get(i)[1]; // 가치
            for(int j=1;j<=K;j++) 
            {
                if(weight>j) // 물건의 무게가 배낭의 최대용량보다 크면
                {
                    dp[i][j]=dp[i-1][j]; // 물건을 집어 넣지 않는다.
                }
                else // 물건의 무게가 배낭의 최대용량보다 작으면
                {	
                	// 물건을 넣지 않는다 vs 물건을 넣는다
                    // 이 중 더 큰 값을 집어넣는다.
                    dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight]+value); 
                }
            }

        }
        // 모든 경우의 수를 따졌을때의 나온 최대가치 출력
        System.out.println(dp[N][K]);

    }
}