💡 이 포스트에는 section3를 진행하는 동안 매일 풀었던 코딩 문제들을 풀고 몰랐던 점이나 부족했던 점을 정리했다!
(누군가에게는 너무 쉬워 하품이 나올 수 있습니다.🥲)
코딩노트 정리하기
section3에서도 section2처럼 아침마다 코딩문제를 풀었다. 확실히 난이도가 저번보다 올라가서 첫문제부터 간신히 풀었는데 레퍼런스를 보고 내가 너무 바보같이 풀었음을 깨달았다...ㅎㅎㅎ
적지 않으면 나중에 큰일날 걸 대비해 중요한 점들을 기록으로 남겨보았다.
저작권으로 인해 몇몇 문제들은 코드가 없을 수도 있다.
1. 세 수의 곱 중에서 최댓값 구하기.
핵심 : 배열에서 최댓값을 구할 때 정렬을 사용하면 간편하다.
놓치지 말기 : 뒤에서부터 곱하면 제일 큰 값이 나오겠지만, 음수도 고려해야 한다.
길이 3개 이상의 배열이 구해지고, 이 중에서 최대값을 찾는 방법에는 여러가지가 있다.
효율적인 방법은 정렬한 후에 가장 큰 수를 곱하는 방법이다.(나는 바보같이 3번이나 반복문을 돌렸었다.🥲)
배열을 정렬하기 위해서는 sort메서드를 사용하는데, 그냥 정렬하면 문자열로 정렬되므로 숫자로 정렬하기 위해 콜백함수를 사용할 수 있다.
아래는 MDN의 sort() 페이지에서 소개한 숫자 정렬 예제이다.
문자열 대신 숫자를 비교하기 위해 compare 함수는 a에서 b를 뺄 수 있습니다. 다음 함수는 배열을 오름차순으로 정렬합니다. (Infinity 및 NaN이 포함되어 있지 않은 경우).
function compareNumbers(a, b) { return a - b; }
이 함수를 sort의 콜백하수로 이용하여 배열을 정렬하고,
맨 뒤가 가장 큰 값이므로 곱하면 된다.
그런데 놓치지 말아야할 건 앞에가 음수인 경우이다.
[-4,-3,-2,1,2,3,4]
위의 배열처럼 만약 앞의 두 요소가 음수이면, 절대값이 가장 크면서 서로 곱하면 양수가 되므로 제일 큰 최대값이 된다.
따라서 (앞의 두개*맨 뒤의 값), (맨 뒤의 3개를 곱한 것) 중에서도 최대값을 비교해야 한다.
const multipleThree = function (numArr) {
//배열을 복사하여 오름차순 정렬한다.
let ascArr = numArr.slice().sort((a, b) => a - b);
let last=ascArr.length;
//뒤의 최대값 3개 곱하기
let case1=ascArr[last-1]*ascArr[last-2]*ascArr[last-3];
//앞2개와 맨 뒤 1개 곱하기
let case2=ascArr[0]*ascArr[1]*ascArr[last-1];
//이 중에서 최대값 반환
return Math.max(case1, case2);
};2. 피보나치 수열 구하기 심화편
핵심 : 재귀함수를 호출하는 횟수를 줄이는 게 좋다.
핵심 : 클로저를 사용하여 필요한 변수를 저장하면 시간복잡도가 줄어든다.
피보나치 수열을 구할 때 재귀함수를 사용해야 한다면 가장 흔하고 쉬운 방법은
return 재귀함수(n-1)+재귀함수(n-2) 이다.
그러나 이 방법은 재귀함수를 두번씩 호출하고, 아래처럼 함수를 중복 호출하게 된다.
- 피보나치 4번째 항 구하기: 재귀함수(3)+재귀함수(2)
- 피보나치 5번째 항 구하기: 재귀함수(4)+재귀함수(3)
-> 재귀함수(3)이 두 번 호출된다.
때문에 이미 구한 피보나치 수열은 저장하고, 매번 새로운 항을 저장하는 방식으로 코딩문제를 풀어야 한다.
그렇다면 코딩문제를 풀 때 함수는 한 번만 실행되는데, 어떻게 변수를 저장해서 계속 사용할 수 있을까?
바로 클로저를 사용하면 된다. 클로저 내부함수는 외부함수의 변수에 접근이 가능하며 그 변수의 데이터가 사라지지 않고 계속 사용할 수 있다. 어려운 말로 어휘적 환경(lexical environment)이 남아있기 때문이다.
정리하자면
외부에 피보나치 배열을 선언하고,
내부의 함수를 리턴하되
내부함수에서는 피보나치 수열을 저장하거나 찾는 구문을 작성하면 된다.
이 내용을 코드로 나타내면 아래와 같다.
function fibonacci(n) {
//피보나치 배열
let fiboArr = [0, 1];
//내부함수: 피보나치 배열을 생성하거나 기존 항을 검색한다.
let infibo =(n)=>{
//기본 피보나치 항이 없을 경우에만 신규 생성
if (fiboArr[n] === undefined) {
fiboArr[n] = infibo(n - 1) + infibo(n - 2);
}
//있다면 기존 항을 검색하여 리턴한다.
return fiboArr[n];
}
//내부함수의 결과를 리턴한다.
return infibo(n);
}3. 버블정렬 하기
핵심 : 두 수의 위치를 바꾸는 방법부터 생각한다.
리팩토링 : 한 번 정렬했을 때 정렬이 일어나지 않았다면 이미 정렬된 것이므로 정렬을 종료한다.
이 문제를 풀기 위해서는 제일 먼저 버블정렬이 뭔지 알아야 한다.
버블정렬은 아래의 그림처럼 두 수를 비교하며 정렬하는 방식이다.
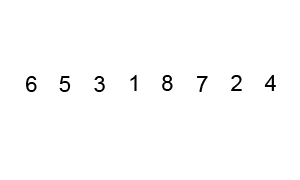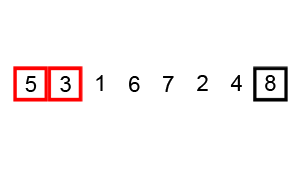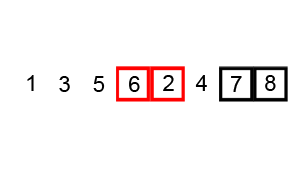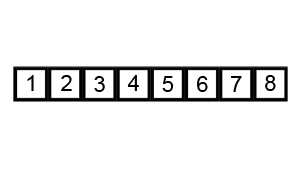
🔗 이미지 출처: https://commons.wikimedia.org/wiki/File:Bubble-sort-example-300px.gif
버블정렬의 순서를 정리하자면 다음과 같다.
- 1회차 순회
- 첫번째 요소와 두번째 요소를 비교하고, 앞의 요소가 크면 뒤의 요소와 자리를 바꾼다.
- 두번째 요소와 세번째 요소를 비교하고, 앞의 요소가 크면 뒤의 요소와 자리를 바꾼다.
- 이 과정을 마지막까지 반복한다.
- 2회차 순회
- 1회차 순회를 매번 정렬된 마지막 요소를 제외하고 반복한다.
이 과정이 곧 의사코드이므로 그대로 작성하면 되는데, 버블 정렬이 처음이라면 두 요소를 바꾸는 것 부터 어려울 수 있다.
두 요소를 바꾸는 방법은 다음과 같이 여러 가지가 있다.
- 임시 변수를 선언하고, 할당하는 방법
- 배열인 경우 구조분해할당을 사용하는 방법
//1. 임시 변수 선언
let temp=;
temp=arr[0];
arr[0]=arr[1];
arr1[1]=temp;
//2. 구조 분해 할당 (배열이므로 사용 가능)
[arr[0], arr[1]]=[arr[1], arr[0]]이 내용을 적용하면 코드는 아래와 같다.
const bubbleSort = function (arr) {
//정렬 필요 여부 판단. false일 경우 정렬할 필요 없음
let needforSort = false;
for (let i = 0; i < arr.length-1; i++) {
for(let j=0; j<arr.length-1-i; j++){
if(arr[j]>arr[j+1]){
//순서 바꾸기 코드 위치. 여기서는 방법1을 사용했다.
//위의 바꾸기 예제를 함수로 처리하여 적용해도 된다.
temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
//정렬이 발생했으므로 상태를 바꾼다.
needforSort=true;
}
}
//정렬할 필요가 없는 경우 정렬을 그만둔다.
if(!needforSort) break;
}
return arr;
};4. 배열의 부분집합 확인하기
핵심 : 배열을 순회할 때 필요없는 부분은 건너뛰어야 한다.
두 배열 중 subset이 universal의 부분집합인지 아닌지, 즉 subsete의 모든 요소가 universal에 속하는지 확인해야 한다.
생각보다 어려웠던 문제였고 시간복잡도도 생각해야 해서 난이도도 있던 문제였다. 내 방식대로 문제를 풀어보니 시간복잡도는 커녕 정답 맞추기도 쉽지 않아서 레퍼런스를 토대로 정리해보았다.
의사코드부터 쉽지 않았기에 예시를 들어 의사코드부터 적어보려고 한다.
예시: universal=[1,2,3,4,8,9], subset=[2,4,6]
- 두 배열을 정렬한다.
시간복잡도를 걱정했는데 의외로 문제를 풀려면 두 배열을 정렬하는 게 더 빨랐다. 왜냐면 배열이 정렬될 경우 요소를 하나씩 비교하는 것보다 시간이 더 단축되기 때문이다. - subset을 순회하며 해당 요소가 universal에 있는지 확인한다.
여기서 이 확인하는 방법에 따라 시간복잡도가 달라진다. - subset의 요소가 universal에 없다면 subset은 universal의 부분집합이 아니다.
위의 과정 중 2번에 많은 부분이 생략되었으며, 레퍼런스에서 2번 부분을 어떻게 풀었는지 다음과 같이 예시로 정리해보았다.
- subset[0]: 2를 base에서 찾을 때, universal의 1부터 찾다가 2를 발견하면 2는 부분집합이므로 탐색을 종료한다.
- subset[1]: 그 다음 4를 찾을 때, universal의 1부터 찾을 필요가 없다. 왜냐하면 두 배열 이미 모두 정렬되었고, universal의 2까지 탐색했기 때문이다. 따라서 universal의 3부터 4가 나올때까지 탐색한다.
- subset[2]: 마찬가지로 6을 탐색할 때 4부터 6이 나올 때까지 찾는다.
그러나 universal에서 탐색하다가 8이 나오는 순간, 더 이상 6을 찾을 수 없으므로 종료한다. 왜냐면 뒤는 이제 6보다 큰 값이 나오기 때문이다.
위의 과정을 정리하면 어떤 변수, 조건이 필요한지 알 수 있다.
- universal의 index: universal에서 매번 처음부터가 아닌, 이전 회차에서 찾았던 index부터 시작한다.
- universal에서 탐색할 때 universal의 각 요소가
- subset의 값과 같은 값이 나올 경우: universal의 index를 저장하고, 탐색을 잠시 멈춘다.
- subset의 값보다 작다면: subset과 같은 값이 나올 때까지 탐색을 계속한다.
- subset의 값보다 크다면: 더 이상 subset값은 없으므로 부분집합은 없으며, 탐색을 종료한다.
코드를 보면 여기까지 이해하는 데 시간이 좀 걸리긴 했지만,
그래도 이를 바탕으로 코드를 작성하면 아래와 같다.
그리고 위의 과정은 복잡하므로 따로 함수로 작성할 수도 있다.
const isSubset = function (universal, subset) {
universal.sort((a, b) => a - b);
subset.sort((a, b) => a - b);
const isInUniversal= (subsetEl, arr, preIdx) => {
for (let i = preIdx; i < arr.length; i++) {
if (subsetEl === arr[i]) return i;
else if (subsetEl < arr[i]) return -1;
}
return -1;
};
let univIdx = 0;
for (let i = 0; i < subset.length; i++) {
univIdx = isInUniversal(subset[i], universal, univIdx);
if (univIdx === -1) return false;
}
return true;
};5. 타일을 놓는 경우의 수 구하기
핵심 : 패턴을 발견할 때까지 반복해보자.
이 문제는 세로2, 가로n의 길이를 가진 바닥에 2X1의 길이를 가진 타일을 놓는 방법을 구하는 문제였다.

그런데 이미지를 보면 이미 가로로 타일을 놓으면 그 아래 똑같이 가로 타일을 놓을 수 밖에 없고, 세로로 놓으면 공간을 꽉 차지하기 때문에 결국 수n을 1과2의 조합으로 나타내는 것과 같은 문제가 된다.
즉,
1은 [1],
2는 [1,1],[2],
3은 [1,1,1],[1,2],[2,1] ...
이런식으로 구할 수 있다.
일단 어떻게 구할지 몰라서
6까지 그림을 그리며 모든 경우의 수를 구해보았다. (...!)
그러면 다음과 같이 규칙을 발견할 수 있다.
- n이 1인 경우: 1가지
- n이 2인 경우: 2가지
- n이 3인 경우: 3가지
- n이 4인 경우: 5가지
- n이 5인 경우: 8가지
- n이 6인 경우: 13가지
1에서 3까지는 타일의 가로가 n인 경우 n가지 경우의 수가 나오지만,
4부터는 그 전 경우와 전전 경우를 더한 가짓수가 나온다.
어디서 많이 본 배열이지 않은가!
바로 피보나치 수열과 비슷하기 때문에 피보나치 수열 심화편에서 풀었던 방법과 같은 방법으로 풀어주었다.
이름만 다르지 코드는 같으므로 따로 코드는 작성하지 않았다.
따라서 코드는 위의 2. 피보나치 수열 심화편을 참고하면 된다.
6. 모양이 같은 객체 탐색하기
핵심 : 반복되는 부분을 찾아 재귀함수를 이용한다.
핵심 : 재귀함수가 리턴하는 값을 각 단계에서 사용할 수 있도록 고려한다.
TIP : 이 방법으로 깊이 우선 탐색이 가능하다.
이 문제는 재귀함수를 이용하면 풀 수 있는 문제였지만 막상 생소한 내용이 같이 있어 바로 어떻게 풀어야할지 생각이 나지 않았다.
찬찬히 생각해보니 반복되는 부분이 있어 재귀함수를 사용했다.
이 문제는 다음과 같이 중첩되는 객체가 있다고 가정한다.
const obj={
title:'alice',
detail: [
{
title:'amy',
detail:[]
},
{
title:'bob',
detail:[
{
title:'jeans',
detail:[]
}
]
}
]
}중첩된 모든 객체를 탐색하여 모든 title값을 배열에 담아 배열을 반환하는 문제였다.
원래 문제에서는 이 객체가 아닌 객체를 생성하는 구문이 적혀있어 직접 완성된 배열의 모양을 보기위해 콘솔 창에 띄우면서 확인해보았다.
즉, 저작권 때문에 수정했지만 원래 문제는 깊이 우선 탐색이라고도 한다.
이 문제는 저번에 재귀함수 코딩문제를 풀 때 객체를 탐색했던 방법으로 풀 수 있다.
각 객체의 중첩 수준만큼 재귀함수를 호출하며 base case는 객체.detail의 값이 빈 배열인 경우이다.
의사코드는 다음과 같다.
- 빈 배열 result를 선언한다.
- 일단 obj의 모든 객체는 title값을 갖고 있으므로 title값을 찾아 result에 삽입한다.
모든 요소에 해당되지만 재귀함수의 base case라고 할 수 있다. - obj.detail의 길이가 0이 아닌 경우: recursive case
- obj.detail의 각 요소의 title을 찾아 빈 배열에 삽입한다.
- 이 각 요소의 title을 찾을 때는 재귀함수를 사용한다.
- 재귀함수는 배열을 리턴하므로, 이 결과를 result에 합친다.
- 합치는 방법은 concat이 있고, spread 문법을 써도 된다.
- 만약 obj.detail의 길이가 0이라면 base case부분만 실행하고 그냥 넘어간다.
- result를 리턴한다.
재귀함수를 사용해야 한다면 base case, recursive case에 집착하게 되고, base는 예외사항이라 생각하게 된다.
그런데 위처럼 모든 경우 base case를 거쳐야 하므로 헷갈릴 때가 있다.
재귀함수를 배웠을 때처럼 base, recursive에 집착하지 말자!
그리고 concat, spread처럼 배열 메서드와 문법도 잊지말고 이렇게라도 활용해주니 도움이 되는 것 같다.
역시 복습을 잘해야 겠다.
이번 문제의 코드는 아래와 같이 정리하였다.
let findTitle = function (obj) {
let result=[];
result.push(obj.title);
if(obj.detail.length!==0){
let arr=obj.detail;
for(let el of arr){
elResult=findTitle(el);
result=[...result, ...elResult];
//위랑 같은 구문: result=result.concat(elResult);
}
}
return result;
};7. 메서드 없이 수의 n승 구하기
핵심 : 분할 정복법을 사용한다.
주의사항 : 94,906,249를 나눈 나머지를 리턴한다.
단순히 구하자면 1부터 n만큼 밑 수를 구하면 된다.
그러나 이 문제는 다음 사항을 고려해야 했다.
- 시간복잡도를 줄여야 했다.
- 계산결과가 컴퓨터가 나타낼 수 있는 수를 넘어설 수 있기에 수를 곱할 때마다 94,906,249로 나눈 나머지를 리턴해야 한다.
2번은 그냥 조건으로 추가하면 되기에 어렵지 않았지만, 1번 사항 때문에 난이도가 많이 올라갔다.
1번 사항을 해결하기 위해 분할 정복법이라는 방법이 있었다.
일단 쉽게 이해할 수 있었던 블로그 링크를 첨부한다.
🔗 About Tech
분할 정복법은 수를 1부터 n까지 다 곱하는 게 아니라,
지수의 성질을 이용해 지수를 반으로 쪼개가면서 계산 횟수를 줄이는 방법이다.
예를 들어 지수는 서로 덧셈뺄셈이 가능하다는 성질을 이용하면 2의 9승을 다음과 같이 나타낼 수 있다.
2^9=2^4*2^4*2^1
이 2의 4승은 또 다음과 같이 나타낼 수 있다.
2^4=2^2*2^2
또 2의 2승은 다음과 같이 나타낼 수 있다.
2^2=2^1*2^1
즉 정리하자면 원래 2를 9번 곱하면 될 것을 3번만에 구할 수 있게 된다.
다만 주의할 점은 지수가 홀수인 경우이다. 이 예외를 잘 처리하여야 한다.
1부터 n까지 곱할 때의 시간복잡도는 O(n) 이지만
위와 같은 방법으로 코드를 작성하면 시간복잡도는 O(logN)이 된다.
시간복잡도가 이만큼이나 줄어드는 것이다.
이 내용은 아래와 같이 코드로 나타낼 수 있다.
function findPower(base, n) {
//어떤 수의 0승은 1이다.
if (n === 0) return 1;
//1. 간단한 방법: 1부터 n까지 곱한다.
/*
let result=1;
for(let i=1; i<=n; i++){
result=result*i;
result=result%94906249; //조건 처리
}
*/
//2. 분할 정복법 사용
let half = parseInt(n / 2); //지수의 반을 구한다.
let halfResult = findPower(base, half); //연산을 반복하기 위해 재귀 사용
let result = (halfResult * halfResult) % 94906249; //조건 처리
//지수가 홀수인 경우 예외 처리
if (n % 2 === 1){
//위의 코드로는 지수가 짝수인 경우만 구해진다. (ex. 지수가 9 일 때 result: 2^4*2^4)
//때문에 홀수면 위 결과에 base^1, 즉 base를 곱해줘야 한다.
return (base * result) % 94906249; //+조건 처리
}else{
return result;
}
}8. 너비 우선 탐색
핵심 :
위의 6번 문제의 객체와 구조가 같은 객체의 title을 찾되, 순서만 다르게 해서 찾는 문제이다.
이번 문제는 6번의 객체를 6번과 다른 순서로 구하는데 아래의 이미지를 보면서 그 순서를 이해하면 덜 어려웠다.
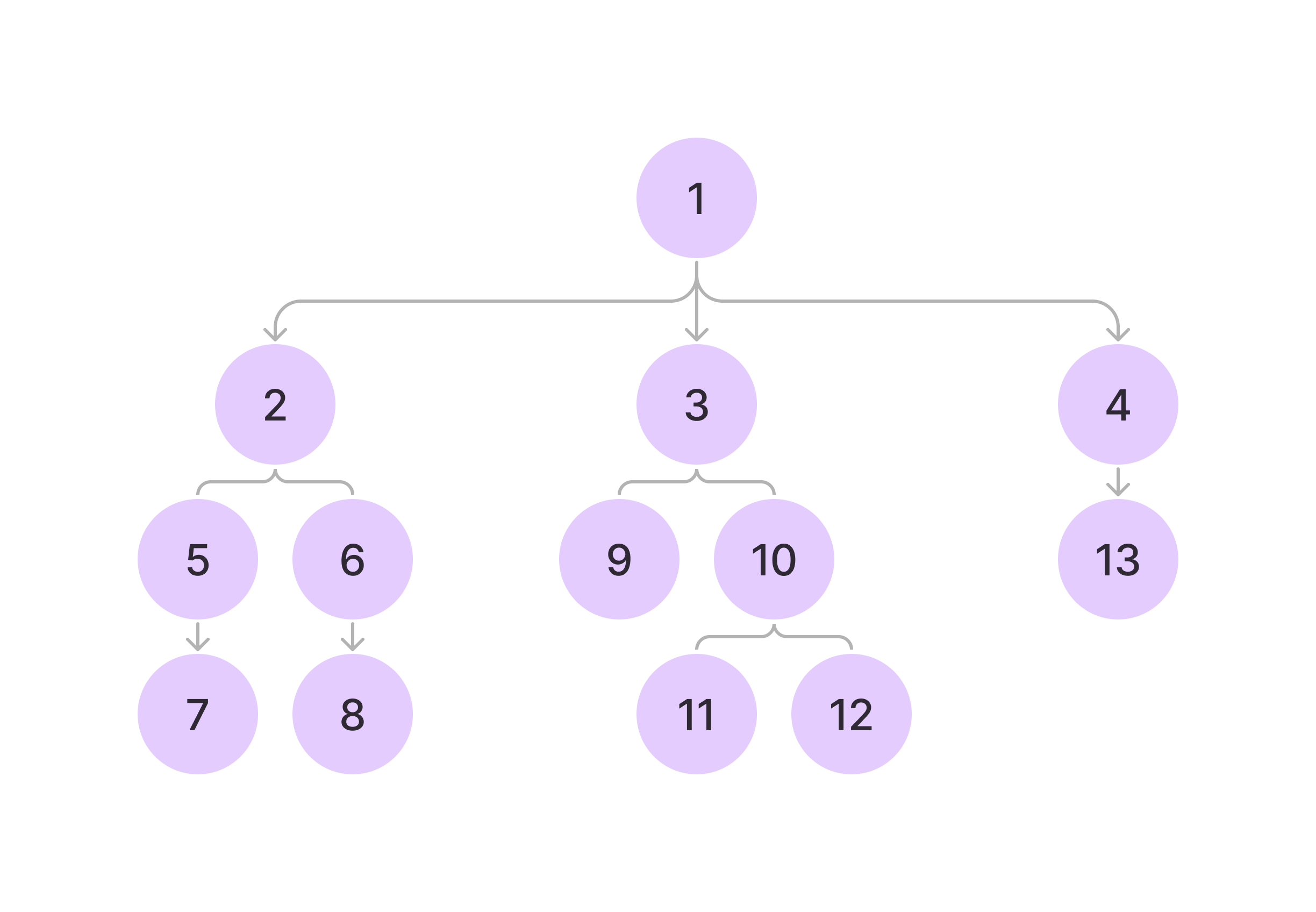
위 이미지에서 1수준, 2수준, 3수준, 4수준을 차례로 탐색하면 순서는
1,2,3,4,5,6,9,0,13,7,8,11,12 가 된다.
6번의 경우 1,2,5,7,6,8,3,9,10,11,12,4,13의 순서로 탐색했었다.
여기서 6번 순서로 탐색하는 것을 깊이 우선 탐색, 위와 같이 수준별로 탐색하는 것을 너비 우선 탐색이라고 한다.
똑같은 구조의 객체지만 해결방법은 전혀 달랐다. 6번처럼 재귀함수를 사용하려다 오히려 더 어려웠던 문제였다.
어려워서 고민하다 레퍼런스를 보았고, 전혀 다른 방식으로 접근해야했다.
의사코드는 다음과 같다.
-
변수 선언
- result: 객체의 title을 담은 배열
- 현재 객체 now: obj.title
- 처리해야할 값 order: now.detail
-
처음 1회차부터 차근차근 진행하기
-
1회차
now에 obj를 할당한다.
배열 order에 now.detail의 요소들을 삽입한다.
result에 now.title을 삽입한다. -
2~n까지 반복
now에 order[0]를 할당한다.
배열 order에 now.detail의 요소들을 삽입한다.
result에 now.title을 삽입한다.
-
-
반복 패턴 정리하기: 처음 order에 obj를 할당하여 시작.
now에 order[0]를 할당하고 order에서 삭제한다.
now.detail을 순회하며 배열 order에 now.detail의 각 요소들을 삽입한다.
result에 now.title을 삽입한다.
-> 이 과정을 order가 0이 될 때까지 반복한다.
의사코드를 코드로 나타내면 아래와 같다.
let findTitle = function (obj) {
let result = [];
let order=[obj];
while(order.length>0){
let now=order.shift(); //배열에서 삭제되면서 삭제된 첫번째 값이 할당된다.
for(let el of now.detail){
order.push(el);
}
result.push(now.title);
}
return result;
};9. 이진탐색
핵심 : 이진탐색이란 주어진 자료를(주로 배열 형태) 반으로 나눠가면 탐색하는 방법이다.
문제를 풀다가 이진탐색을 활용하라는 문구가 나왔다. 이진탐색을 몰랐기 때문에, 여기선 이진탐색에 대한 설명과 이진탐색을 코드로 나타냈을 때를 정리했다.
이진탐색은 배열을 반으로 나눠가며 원하는 값을 찾는 방법이다.
의사코드는 다음과 같다.
- 이진탐색을 하기 위해선 배열이 먼저 정렬되어 있어야 한다.
- 배열을 중간 인덱스를 찾는다.
- 중간 인덱스가 찾는 값일 경우: 탐색을 종료한다.
- 중간 인덱스가
- 찾는 값보다 작을 경우 왼쪽 반을 탐색한다. 왼쪽 배열만을 남긴다.
- 찾는 값보다 클 경우 오른쪽 반을 탐색한다. 오른쪽 배열만을 남긴다.
- 다시 탐색하기 위해 남긴 배열에서 중간 인덱스를 새로 정한다.
- 1~4를 반복해가며 원하는 값을 찾는다.
이진탐색은 시간 복잡도가 O(logN)으로 일반적인 선형탐색보다 빠르다.
이 이진탐색을 코드로 나타내면 아래와 같다.
const binarySearch = function (array, target) {
let lowIdx = 0, highIdx = array.length - 1;
while (lowIdx <= highIdx) {
let midIdx = parseInt((lowIdx + highIdx) / 2);
if (array[midIdx] === target) {
return midIdx;
}else if(target<array[midIdx]){
highIdx=midIdx-1;
}else{
lowIdx=midIdx+1;
}
}
return -1;
};10. 스택과 큐의 적절한 사용
핵심 : 가장 나중의 것을 먼저 처리해야 한다면 스택을, 순서대로 처리해야 한다면 큐를 사용한다.
관련된 문제는 저작권의 문제로 등록하지 않았고, 문제를 풀기 위해 스택과 큐 자료구조를 알맞게 사용해야 하므로 적었다.
이 문제를 풀려면 section4 의 unit 1에서 배우는 스택, 큐를 사용해야 했다.
그래서 section4를 배우기 시작한 지금에서야 이해를 할 수 있었다.
복잡한 데이터를 한 번에 처리해야하고, 동시에 여러 데이터를 처리해야할 때는 마치 연습장처럼, 공책처럼 데이터를 따로 보관할 장소가 필요하다. 이 때
- 여러 데이터를 순회하면서 검사해야할 데이터를 따로 빼놓아야 할 때
상황에 따라 스택 또는 큐를 사용해야 한다.
어떤 자료구조를 사용할지는 다음과 같은 기준으로 나눠서 검사한다.
- 여러 데이터를 처리할 때 가장 나중의 것을 먼저 처리해야 한다면:
스택을 사용한다. - 여러 데이터를 처리할 때 순서대로 처리해야 한다면:
큐를 사용한다.
잘 모를 때는 단순하게 if등의 조건문과 반복문만을 사용해서 문제를 풀었는데, 위의 스택 또는 큐의 자료구조를 활용하니 큰 도움이 되었다.
노트 정리 후 느낀점
데일리 코딩의 내용이 점점 어려워지고 있다. JS, React 등의 공부와는 다르게 문제를 풀면 풀수록 맞는 문제가 적어지고 이해하기도 어려워지다보니 여기에 초점을 맞추다보면 다른 공부가 힘들다. 그래서 코딩테스트 준비에 집중해야할지, 기본 공부에 집중해야할지 고민이었다.
그런데 생각해보니 기본 개념 공부가 안되었는데 코딩테스트 준비에 집중해야 한다는 게 말이 안되는 것 같다. 다른 동기들은 계속 코딩 테스트 준비에 집중하는데 그 흐름을 따라가야 하는게 맞을지? 잘 모르겠다.
- 이번의 부족한 점
- 이제는 레퍼런스마저 이해하는 데 어렵다.
- 일단 기본이 되는 개념-검색, 정렬 등등의 개념을 먼저 공부할 필요를 느꼈다.
- 부족한 점 보완하기
- 문제를 풀 수 없다면, 일단 레퍼런스를 이해하자.
- 기본 개념을 알아야 하는 문제라면 블로그에 먼저 정리하자.
이제는 과제를 제시간에 제출하기도 벅차고 공부량도 점점 많아져서 쉽지가 않다.
중요한 건 내 멘탈이 흔들리지않고 평정심을 유지하는 것이다.
냉정하게 생각해서 부족한 점을 보완해보자.
🤓

