1. Introduction

Suggesting Local Implicit representation for Super resolution of Arbitrary scale(LISA), which can obtain a continuous representation of audio and enable super resolution for arbitrary scale factor. (Current approaches treat audio as discrete data)

LISA

Encoder

Corresponds each chunk of audio to a latent code parameterizing a local input signal around the chunk. -> Don't get it. Isn't local input the chunk?

Decoder

Takes 1. a continuous time coordinate and 2. the neighboring set of latent codes around the coordinate, and predicts the value of signal at the coordinate

Process

1. Down sample to the input resolution.
2. Generate super resolution tasks of random scale up to the original resolution.
3. Use a stochastic measure of audio discrepancy between entire reconstructed and original signals in waveform and spectrogram
4. Closer discrepancy gets higher random weight
   Thus, local latent code of a chunk captures a characteristic of the global audio signal, while focuses on the local signal around the chunk. -> HOW?

Advantages

Having the local implicit representation in terms of the low latency and the arbitrary scale factor as input audio is often streaming in audio super resolution. -> What does 'streaming' mean in this context? Flows?

2. Method

Compositions

• $F(t)$ : Audio
• $t \in \mathbb{R}, \ t=t_i$'s in every sampling period $\frac{1}{R_{in}}$, where $R_{in}>0$ is input resolution
• $F(t_i)$ : local part of discrete samples around $t$
• $g_\phi$ : encoder with parameter $\phi$
• $f_\theta$ : decoder with parameter $\theta$
• $z_i \coloneqq$ $g_{\phi}(F(t_i−k), \cdots, F(t_i+k))$ i.e. (2k+1) samples around time $t_i$
• $z(t) \coloneqq (z_{i(t)−1}, z_{i(t)} , z_{i(t)+1})$, where $i(t) \coloneqq \arg\min_i |t − t_i|$, i.e. $i(t)$ is the closest index to $t$
• $\hat{F}(t) := f_θ(t − t_{i(t)}; z(t)) ≈ F(t)$
  : continuous representation

LISA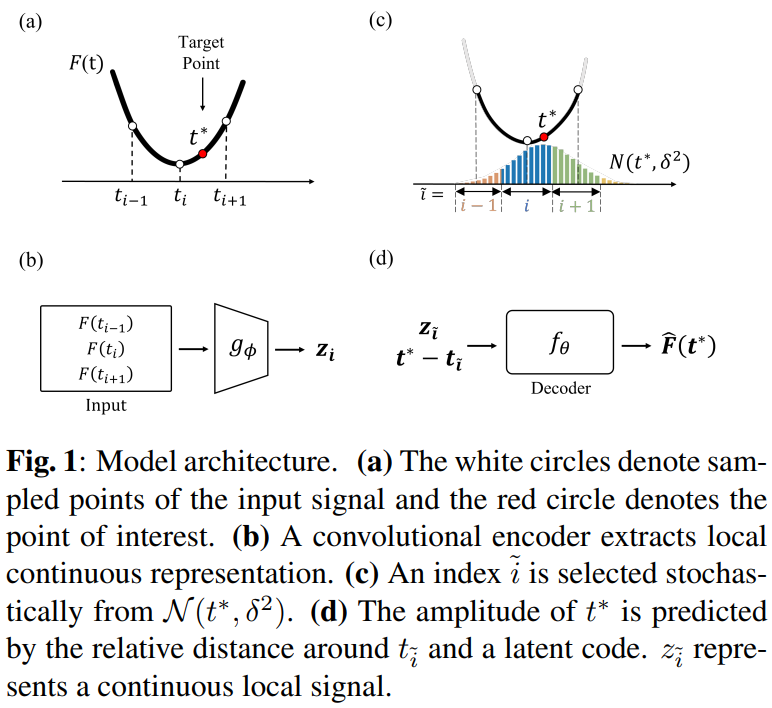

Note that, $\tilde{i}=t(i)$

Output prediction

By putting the sequence of time coordinates every $\frac{1}{R_{out}}$ to $\hat{F}(\cdot)$
-> Don't get it

2.1 Model Architecture

Encoder $g_\phi$

1. Convolutional network
   • Induces temporal correlation, by summarizing a few consecutive data points.