해시 테이블(Hash Table)
해싱(Hashing)
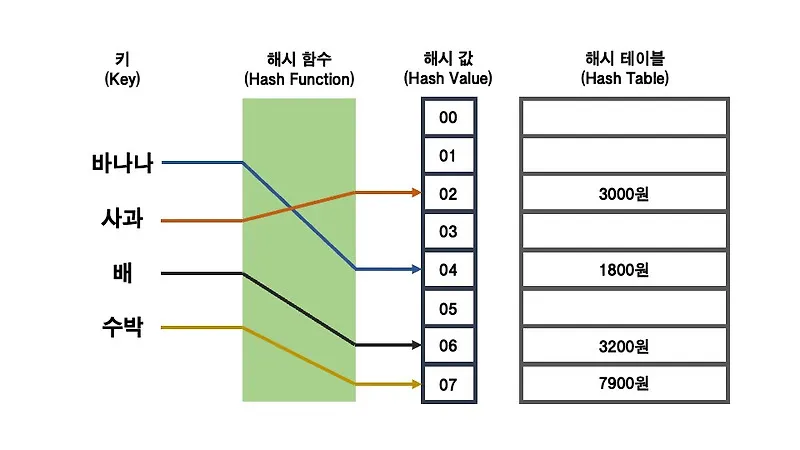
해싱은 크기와 형식이 다양한 입력값을 고정된 크기의 해시값으로 변환하는 기법이다. 이 해시값은 해시 테이블에서 데이터를 저장할 위치를 결정하는 데 사용된다.
특징
- 입력값의 크기와 상관없이 일정한 크기의 해시값이 생성된다.
- 해시 함수(Hash Function)를 이용해 변환을 수행한다.
- 평균적으로 검색, 삽입, 삭제가 O(1)의 시간 복잡도를 가진다.
해시 테이블(Hash Table) 개요
해시 테이블은 키(key)와 값을 저장하는 배열 기반의 자료구조로, 키를 해시 함수에 적용하여 얻은 해시값을 인덱스로 사용해 빠르게 데이터를 검색할 수 있다.
주요 특징
- 평균적으로 O(1)의 시간 복잡도로 검색, 삽입, 삭제가 가능하다.
- 비교적 단순한 구조로 동작한다.
- 연결 리스트나 이진 탐색 트리보다 빠른 성능을 제공할 수 있다.
주요 활용 사례
- 딕셔너리(Dictionary) : 파이썬의
dict등 - 집합(Set) : 중복 없는 데이터 관리
- 캐시(Cache) : 빠른 데이터 접근
- 데이터베이스 인덱스 관리
- 암호학(Cryptography)
해시 테이블의 구성 요소
- Key(키) : 검색, 삽입, 삭제의 기준이 되는 값
- Hash Function(해시 함수) : 키를 입력받아 테이블의 인덱스를 반환하는 수학적 공식
- Hash Table(해시 테이블) : 해시값을 인덱스로 사용하여 데이터를 저장하는 배열
해싱 동작 방식 예시
문제 상황
다음 문자열 집합 {“ab”, “cd”, “efg”}를 해시 테이블에 저장한다고 가정한다.
단계별 설명
- 각 문자에 숫자 할당
"a" = 1,"b" = 2,"c" = 3, ...
- 문자 코드 합산
"ab" = 1 + 2 = 3"cd" = 3 + 4 = 7"efg" = 5 + 6 + 7 = 18
- 해시 함수 적용
- 테이블 크기 = 7
sum(string) % 7로 인덱스 결정"ab" ➝ 3 % 7 = 3"cd" ➝ 7 % 7 = 0"efg" ➝ 18 % 7 = 4
해시 함수(Hash Function)
해시 함수는 키를 입력받아 해시 테이블의 인덱스를 반환하는 역할을 한다.
좋은 해시 함수의 조건
- 연산이 효율적이어야 한다.
- 키 값이 해시 테이블에 균등하게 분포하도록 해야 한다.
- 서로 다른 키가 동일한 인덱스로 매핑되는 충돌(Collision)을 최소화해야 한다.
대표적인 해시 함수 방식
- 나눗셈 방법(Division Method)
- 키 값을 테이블 크기로 나눈 나머지를 인덱스로 사용한다.
- 공식 :
index = key % table_size - 테이블 크기 : 소수(prime number)를 사용하는 것이 일반적이다.
왜 모듈러 연산에서 소수를 사용하나?
테이블 크기를 소수가 아닌 값으로 설정하면 특정 패턴의 키들이 동일한 인덱스로 해싱될 가능성이 커진다.
소수를 사용하면 해시값이 테이블 전체에 더 균등하게 분포되어 충돌 가능성을 줄일 수 있다.
예를 들어, 테이블 크기가 7(소수)일 때:
"ab"→3 % 7 = 3"cd"→7 % 7 = 0"efg"→18 % 7 = 4
충돌(Collision)
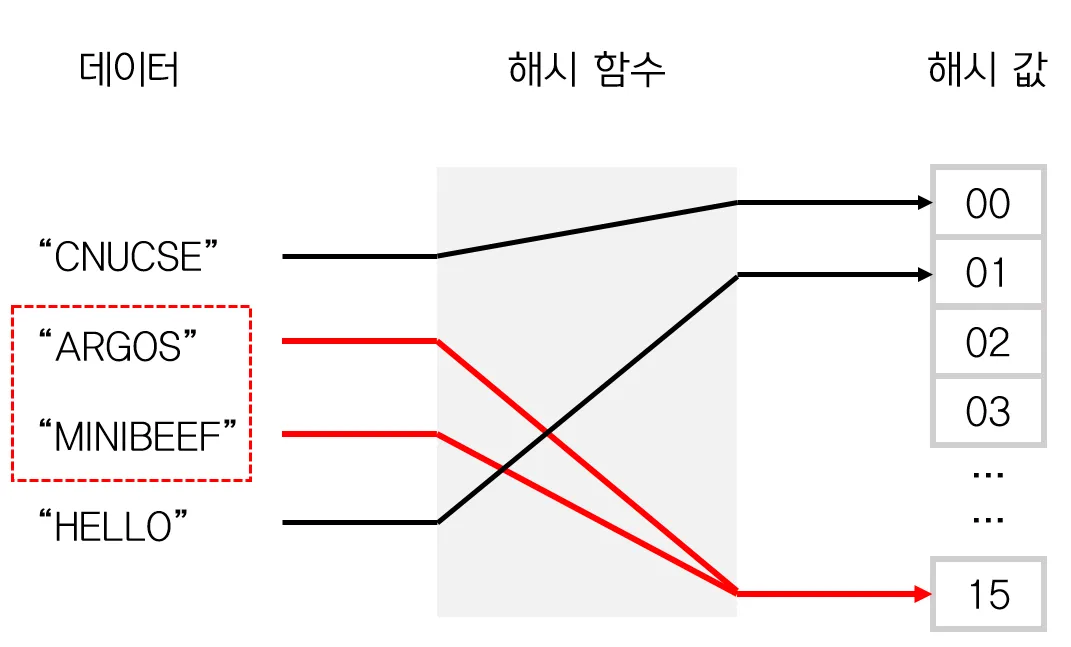
충돌이란 서로 다른 키가 같은 인덱스로 해싱되는 경우를 의미한다.
예시
"ab"→3"ba"→3"ab"와"ba"가 동일한 해시값3을 갖기 때문에 충돌 발생
충돌이 많아지면 탐색/삽입/삭제 성능이 저하될 수 있다.
충돌 해결 방법
- 체이닝(Chaining) 기법
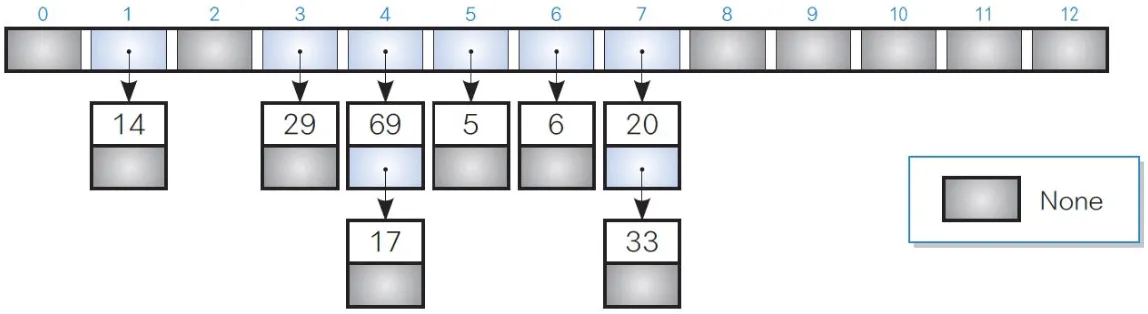
- 같은 인덱스에 여러 개의 데이터를 연결 리스트(Linked List)로 저장하는 방식
- 충돌이 발생하면 해당 인덱스의 리스트에 데이터를 추가하는 형태
- 단점 : 해시 테이블의 메모리 사용량 증가
- 오픈 주소법(Open Addressing) 기법
- 충돌 발생 시, 빈 슬롯을 찾아 데이터를 저장하는 방식
- 대표적인 기법 :
- 선형 탐색(Linear Probing) :
(index + 1) % table_size로 다음 빈 공간을 찾음 - 이차 탐색(Quadratic Probing) :
(index + i^2) % table_size방식 사용 - 이중 해싱(Double Hashing) : 두 개의 해시 함수를 활용하여 충돌을 해결
- 선형 탐색(Linear Probing) :
오픈 주소법은 별도의 연결 리스트를 사용하지 않지만, 테이블이 가득 차면 성능이 급격히 저하될 수 있다.
Load Factor(부하 계수)
해시 테이블이 얼마나 차 있는지를 나타내는 값으로, 다음과 같이 계산된다.
공식 : Load Factor = (저장된 항목 수) / (테이블 크기)
- Load Factor가 높아질수록 충돌 빈도가 증가하여 성능이 저하된다.
- 일반적으로 0.75를 초과하면 Rehashing을 수행한다.
Rehashing(재해싱)
Rehashing은 해시 테이블의 크기를 증가시키고 기존 데이터를 새로운 테이블에 다시 저장하는 과정이다.
동작 원리
- Load Factor가 0.75 이상이 되면 테이블 크기를 2배로 확장한다.
- 기존 데이터를 새로운 테이블에 다시 해싱하여 저장한다.
- 이를 통해 충돌을 줄이고 성능을 유지할 수 있다.
정리
- 해싱은 키를 해시값으로 변환하여 데이터를 빠르게 검색, 삽입, 삭제하는 기법
- 해시 테이블은 평균적으로 O(1)의 시간 복잡도를 가지며 딕셔너리, 캐시, DB 인덱스 등에 활용됨
- 해시 함수는 데이터를 균등하게 분포시키고 충돌을 최소화해야 함
- 충돌이 발생하면 체이닝(연결 리스트 사용) 또는 오픈 주소법(빈 슬롯 탐색) 으로 해결 가능
- Load Factor가 일정 수준을 초과하면 Rehashing을 통해 테이블 크기를 증가시킴

