교육 정보
- 교육 명: 경기미래기술학교 AI 교육
- 교육 기간: 2023.05.08 ~ 2023.10.31
- 오늘의 커리큘럼:
파이썬 기반의 머신러닝 이해와 실습 (06/14~07/07)- 강사: 양정은 강사님
- 강의 계획:
1. 개발환경세팅 - IDE, 가상환경
2. 인공지능을 위한 Python
3. KNN 구현을 위한 NumPy
4. K Nearest Neighbors Classification 구현
5. K Means Clustering Mini-project
6. Scikit-learn을 이용한 SVM의 학습
7. Decision Tree의 개념
8. ID3 Algorithm
9. Impurity Metrics - Information Gain Ratio, Gini Index
10. Decision Tree 구현
11. 확률 기초
12. Bayes 정리 예시
13. Naive Bayes Classifier
14. Gaussian Naive Bayes Classifier
Naive Bayes Classifier
- Bayes 통계학을 기본으로 함
- 넷플릭스의 취향 추천 알고리즘
- 실생활하고 연관이 많은 알고리즘 (날씨 예측, 자율주행 자동차 등)
- 마치 사람처럼 새로운 정보를 계속 받아들이고 판단을 업데이트
확률과 통계
❗ 무조건 지금 이해 할 것
-
조건부 확률(conditional prodability)
- P(A|B) A라는 사건의 발생확률이 B라는 사건에 의해 바뀜
1~100중 1개 선택 P(A) = 1/100
일의 자리가 5이라는 조건이 B이면 P(A|B) = 1/10
짝수라는 조건이 C이면 P(A|C) =1/2
- P(A|B) A라는 사건의 발생확률이 B라는 사건에 의해 바뀜
-
Likelihood(가능성, 우도)
- 어떤 클래스에서 어떤 현상이 관측될 확률
ex. 쇼핑/아이쇼핑을 클래스로 두고 나누고자 할때클래스는 구매O,X이고 어떤 현상은 점원에게 말을 거는가 안거는가가 될 수 있음
구매(B) 구매X(¬B), 말걸기(T), 말걸기X(¬T)
P(T|B), P(¬T|B)
P(T|¬B), P(¬T|¬B)
- 어떤 클래스에서 어떤 현상이 관측될 확률
-
Posterior probability(사후확률)
- 어떤 현상이 관측되었을때 그게 특정 클래스에서 발생했을 확률
구매(B) 구매X(¬B), 말걸기(T), 말걸기X(¬T)
P(B|T), P(¬B|T)
P(B|¬T), P(¬B|¬T)
likelihood랑 선후관계가 반대
- 어떤 현상이 관측되었을때 그게 특정 클래스에서 발생했을 확률
Bayes 정리
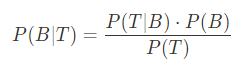
P(B|T): Posterior Probability - 구하고 싶은 값 (B, ¬B)
P(T|B): likelihood - 하나의 클래스에서(B, ¬B) 현상(T)가 일어날 확률
P(B): prior probability - 구하고 싶은 값(B, ¬B)에 대해 알고있는 확률
P(T): normalization constant
→ 우리가 알고싶은것: P(B|T) - 말을 걸때의 구매 확률
→ 나머지 3개는 구하기 쉬운 값이고 저 값은 구하기 어려운 값이므로 구하기 쉬운데이터에서 모르는 데이터를 구하고자 함
첫번째 예시
백화점 직원으로써 판매를 늘리기 위해 고객이 진짜 살지말지 판단하고 싶은 상황 (구매의지)
- 구매의지가 있는지 판단하기위한 정보가 필요: 여기서는 말을거는지 안거는지
- 구매의지가 있는지 없는지 (B, ¬B)
- 말을거는지 안거는지 (T, ¬T)
- prior probability (사전 확률)
- 경험적인 근거를 통해서 사전 확률 설정 (어떤 사건이 일어나기 전 클래스에 대한 확률)
- 전체 고객의 20%가 구매를 한다
B:¬B = 2:8
P(B) = 0.2, P(¬B) = 0.8 (전체 확률 1)
→ 고객이 들어온 직후의 구매 예측 확률은 0.2인 상태 (사전 확률, 아무일도 생기지 않았을때의 확률)
- likelihood (원인에 따른 결과의 확률), P(결과|원인)
- 구매한 사람중에 90%가 말을 걸었다면
P(T|B) = 0.9
P(¬T|B) = 0.1 - 안사는데 말을 거는사람이 30%이면
P(T|¬B) = 0.3
P(¬T|¬B) = 0.7
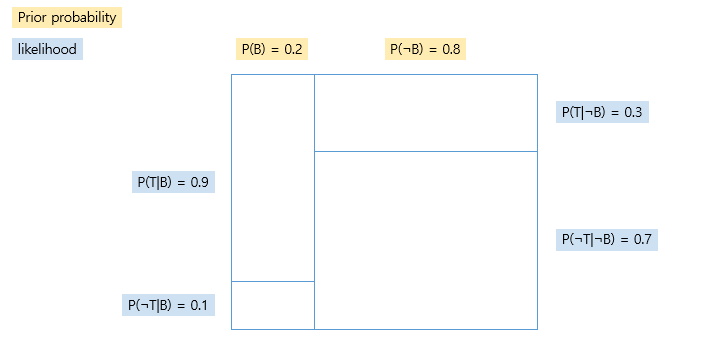
- 위에있는 Prior Probability가 우리가 알고싶은 값 P(B), P(¬B)
- joint probabilty P(A∩B)
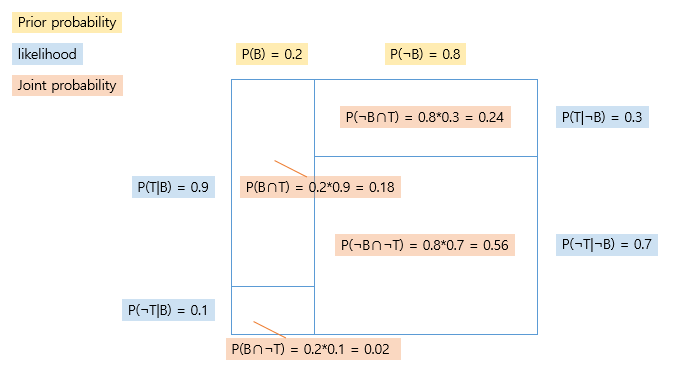
- 사후 확률 (결과로부터 원인을 추정, 베이즈 추정) P(원인|결과)
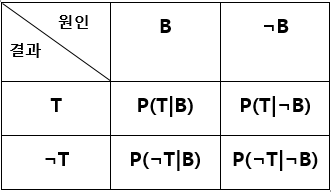
결과와 원인은 위 표 참고 - 원인이 항상 Class 값이 됨
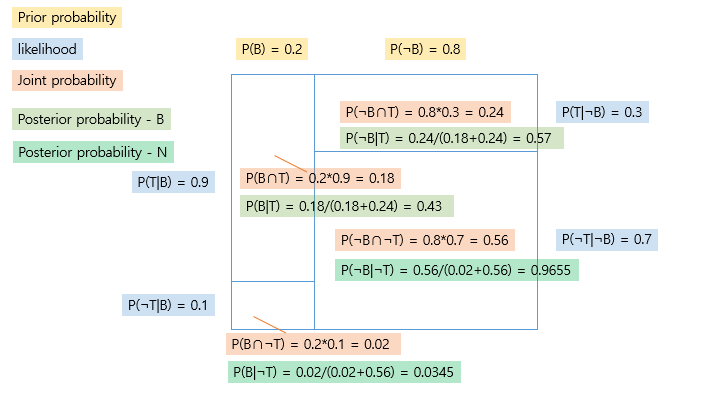
- 손님이 말을 거는 경우
= T 사건 발생 → P(B∩T), P(¬B∩T) 영역만 남음
p(B|T) + P(¬B|T) = 1
∴ 말을 건다는 정보를 획득하고 나서의 확률은 아래와 같아짐
p(B|T) = 0.18/(0.18+0.24) = 0.428
P(¬B|T) = 0.24/(0.18+0.24) = 0.572
→ 고객이 말을 걸었을때 구매 확률을 업데이트 함: Bayes Update
: 새로운 정보에 의해서 사전 확률을 사후 확률로 업데이트 하는것
두번째 예시 (암 진단 키트)
- 양성인 사람이 양성으로 나올 확률 95%
- 양성인 사람이 음성으로 나올 확률 5%
- 건강한 사람이 양성이 나올 확률이 2%
- 건강한 사람이 음성이 나올 확률 98%
암에 걸린 사람(C), 암이 걸리지 않은 사람 (¬C)
키트를 했을때 양성(P), 키트를 했을때 음성(N)로 할때
-
Prior probability & likelihood
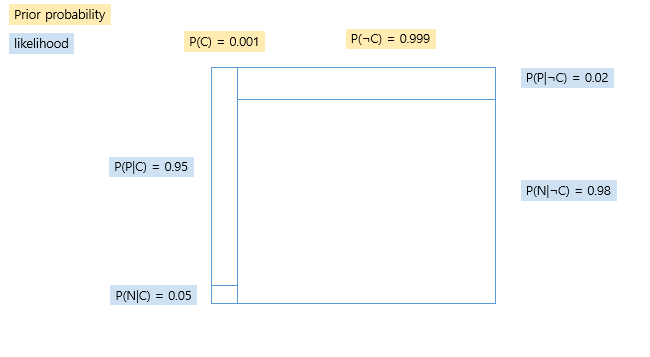
-
Joint probability
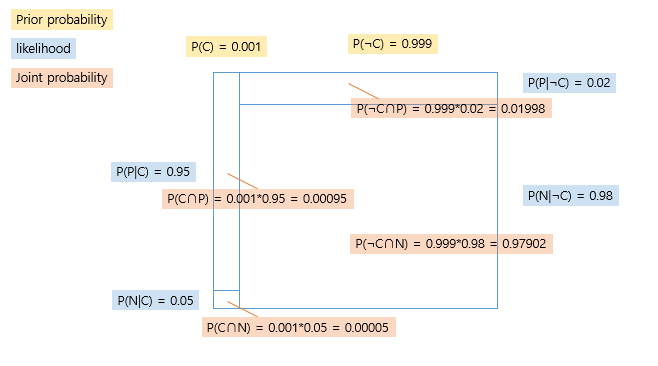
-
Posterior probability
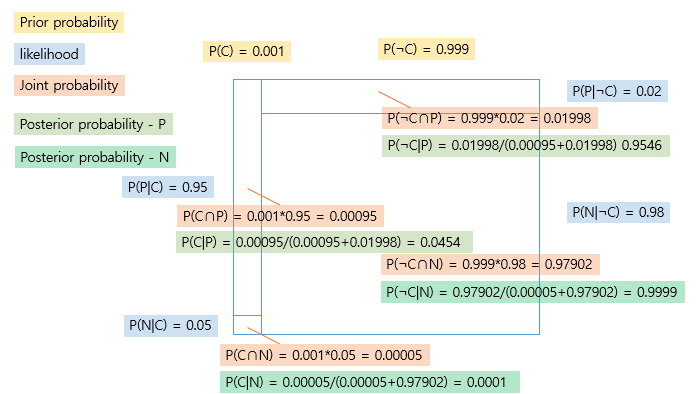
- 진단 전 0.0001의 확률(Prior Probability)이었던 암 확률이 진단 키트에서 양성이 나올 경우 0.0454의 확률(Posterior Probability)로 업데이트 됨
→ 결과로부터 원인을 추청
세번째 예시 (확률의 확률 개념 도입)
Bayes 추정을 통해 특정 부부의 자녀 성별 확률을 추정해보기
- Class 정보
여아를 낳을 확률을 기준으로
class1: 0.6
class2: 0.5
class3: 0.4
인 확률을 가지는 클래스들이 있음
- 확률의 확률 개념 도입
- Class가 확률에 관한 분류이고, 그 자체로도 확률을 가지는 경우
- 자녀 정보가 없는 경우 각각 1/3 확률을 가진다고 가정 할 수 있음
이때 첫째가 여아인 부부가 위 3개의 클래스 중 어떤 클래스에 속할 확률을 추정하면 아래와 같음
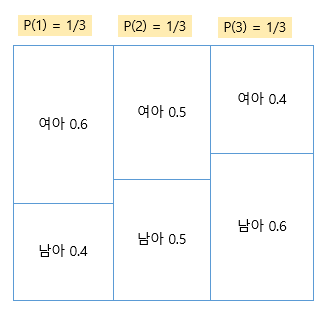

첫째가 여아라는 정보를 통해 이 부부의 클래스 확률 자체가 업데이트 됨
