머신러닝(파이썬) - Naive Bayes Classifier _확률 업데이트(2)

교육 정보

• 교육 명: 경기미래기술학교 AI 교육
• 교육 기간: 2023.05.08 ~ 2023.10.31
• 오늘의 커리큘럼:
  파이썬 기반의 머신러닝 이해와 실습 (06/14~07/07)
• 강사: 양정은 강사님
• 강의 계획:
  1. 개발환경세팅 - IDE, 가상환경
  2. 인공지능을 위한 Python
  3. KNN 구현을 위한 NumPy
  4. K Nearest Neighbors Classification 구현
  5. K Means Clustering Mini-project
  6. Scikit-learn을 이용한 SVM의 학습
  7. Decision Tree의 개념
  8. ID3 Algorithm
  9. Impurity Metrics - Information Gain Ratio, Gini Index
  10. Decision Tree 구현
  11. 확률 기초
  12. Bayes 정리 예시
  13. Naive Bayes Classifier
  14. Gaussian Naive Bayes Classifier

Naive Bayes Classifier

Bayes 이론 Pandas 적용하기

• 연속적으로 업데이트를 수행할 수 있게 수정하기 (if문 사용)

def update_bayesian_table(data, likelihood):
    if 'posterior' in data.columns:
        data['prior'] = data['posterior']
    data['likelihood'] = likelihood
    data['unnorm'] = data['prior'] * data['likelihood']
    norm_constant = data['unnorm'].sum()
    data['posterior'] = data['unnorm'] / norm_constant
    return data

table = pd.DataFrame(index=['spam', 'ham'])
table['prior'] = 0.5, 0.5
print('\n', 'Before Update: ')
print(table)

table = update_bayesian_table(table, likelihood=[0.6, 0.2])
print('\n', 'After 1st Update: ')
print(table)

table = update_bayesian_table(table, likelihood=[0.4, 0.05])
print('\n', 'After 2nd Update: ')
print(table)
#
#결과 
 Before Update: 
      prior
spam    0.5
ham     0.5

 After 1st Update: 
      prior  likelihood  unnorm  posterior
spam    0.5         0.6     0.3       0.75
ham     0.5         0.2     0.1       0.25

 After 2nd Update: 
      prior  likelihood  unnorm  posterior
spam   0.75        0.40  0.3000       0.96
ham    0.25        0.05  0.0125       0.04

Process finished with exit code 0

• Bayes 특징
  • 이전 정보를 저장할 필요가 없음
  • 정보가 들어오는 순서가 상관 없음
    • Decision tree 는 Feature importance를 구분할때 사용되므로 이를 통해 Bayes에 어떤 정보를 먼저 가져올지 선택할 수 있음

예제

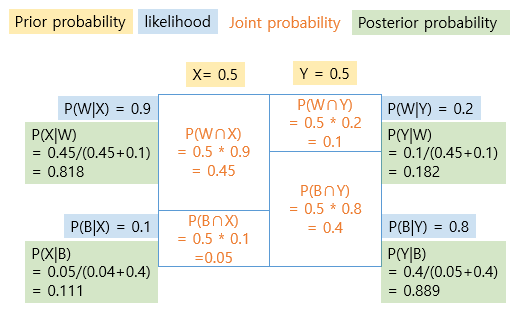
• X, Y 단지 (X에 흰공 9개 검은공 1개) (Y에 흰공 2개 검은공 8개)

1. 공을 하나 꺼냈을때 검은색이었다면 그 단지가 X일 확률, Y일 확률 구하기

1-1. 그림

1-2. 코드

def update_bayes(table, likelihood):
    if 'posterior' in table.columns:
        table['prior'] = table['posterior']
    table['likelihood'] = likelihood
    table['unnorm'] = table['prior'] * table['likelihood']
    table['posterior'] = table['unnorm']/table['unnorm'].sum()
    return table
    
table = pd.DataFrame(index=['X', 'Y'])
table['prior'] = 0.5, 0.5
table = update_bayes(table, likelihood=[0.1, 0.8])

print(table)
#
# 결과 
   prior  likelihood  unnorm  posterior
X    0.5         0.1    0.05   0.111111
Y    0.5         0.8    0.40   0.888889

1-3. 수식

2. 공을 하나 꺼냈을때 흰색이었다면 그 단지가 X일 확률, Y일 확률 구하기
2-1. 그림

2-2. 코드

def update_bayes(table, likelihood):
    if 'posterior' in table.columns:
        table['prior'] = table['posterior']
    table['likelihood'] = likelihood
    table['unnorm'] = table['prior'] * table['likelihood']
    table['posterior'] = table['unnorm']/table['unnorm'].sum()
    return table
    
table = pd.DataFrame(index=['X', 'Y'])
table['prior'] = 0.5, 0.5
table = update_bayes(table, likelihood=[0.9, 0.2])

print(table)
#
# 결과
   prior  likelihood  unnorm  posterior
X    0.5         0.9    0.45   0.818182
Y    0.5         0.2    0.10   0.181818

2-3. 수식

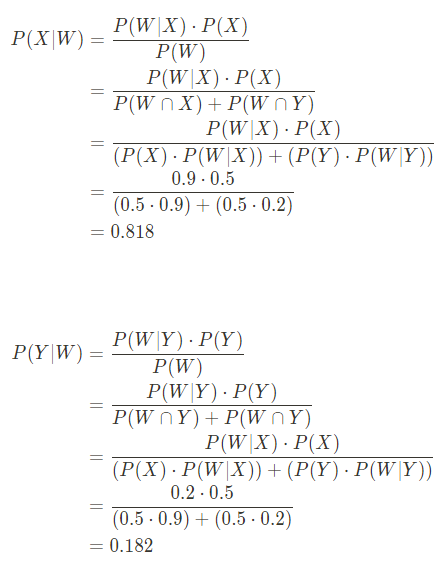
3. 공을 두번 꺼냈을때 검은색-검은색/검은색-흰색일 경우 그 단지가 X일 확률, Y일 확률 구하기
(뽑은 공은 다시 넣음)

3-1. 그림

3-2. 코드

def update_bayes(table, likelihood):
    if 'posterior' in table.columns:
        table['prior'] = table['posterior']
    table['likelihood'] = likelihood
    table['unnorm'] = table['prior'] * table['likelihood']
    table['posterior'] = table['unnorm']/table['unnorm'].sum()
    return table

print('공을 두번 뽑았을 때 BB인 경우')
table = pd.DataFrame(index=['X', 'Y'])
table['prior'] = 0.5, 0.5
table = update_bayes(table, likelihood=[0.1, 0.8])
table = update_bayes(table, likelihood=[0.1, 0.8])
print(table)
print()
print('공을 두번 뽑았을 때 BW인 경우')
table = pd.DataFrame(index=['X', 'Y'])
table['prior'] = 0.5, 0.5
table = update_bayes(table, likelihood=[0.1, 0.8])
table = update_bayes(table, likelihood=[0.9, 0.2])
print(table)

#
#결과
공을 두번 뽑았을 때 BB인 경우
      prior  likelihood    unnorm  posterior
X  0.111111         0.1  0.011111   0.015385
Y  0.888889         0.8  0.711111   0.984615

공을 두번 뽑았을 때 BW인 경우
      prior  likelihood    unnorm  posterior
X  0.111111         0.9  0.100000       0.36
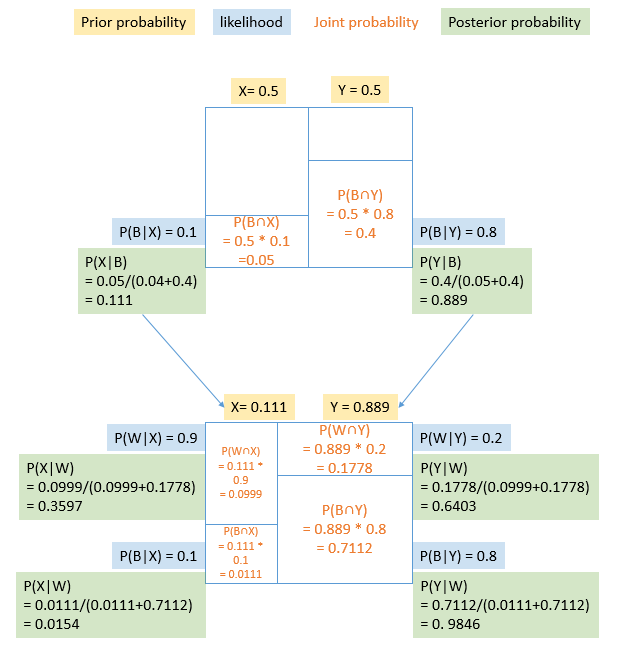
Y  0.888889         0.2  0.177778       0.64

4. 공을 3번 꺼냈을때 검은색-검은색-흰색일 경우 그 단지가 Y일 확률 구하기
(뽑은 공은 다시 넣음)

4-1. 그림

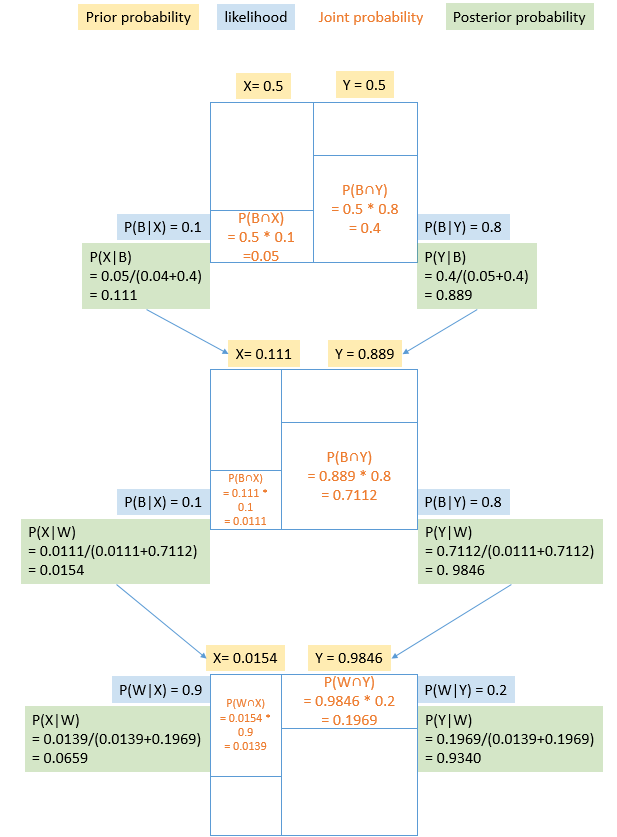
4-2. 코드

def update_bayes(table, likelihood):
    if 'posterior' in table.columns:
        table['prior'] = table['posterior']
    table['likelihood'] = likelihood
    table['unnorm'] = table['prior'] * table['likelihood']
    table['posterior'] = table['unnorm']/table['unnorm'].sum()
    return table

print('공을 세번 뽑았을 때 BBW인 경우')
table = pd.DataFrame(index=['X', 'Y'])
table['prior'] = 0.5, 0.5
table = update_bayes(table, likelihood=[0.1, 0.8])
table = update_bayes(table, likelihood=[0.1, 0.8])
table = update_bayes(table, likelihood=[0.9, 0.2])
print(table)
print()
#
#결과
공을 세번 뽑았을 때 BBW인 경우
      prior  likelihood    unnorm  posterior
X  0.015385         0.9  0.013846   0.065693
Y  0.984615         0.2  0.196923   0.934307

→ 동일한 likelihood를 가질때 관측을 많이하면 할수록 정확도가 올라가서 무한대로 시행할 경우 하나의 확률이 1에 수렴

Naive Bayes의 특징

• 원래 A와 B가 서로 독립적(independant)일 경우에만
  
  이지만 Naive Byes에서는 A와 B가 서로 독립적이지 않더라도(dependant) 독립적이라고 가정하는 특징이 있음
  
  
  <참고>
  📕 dependant와 independant
• independant
  : 동전 던지기 + 주사위 던지기 (서로 영향 X)
• dependant
  : '투자'라는 단어가 이메일에 들어있을 확률 & '수익률'이라는 단어가 이메일에 들어있을 확률
  ('투자'라는 단어가 이메일에 있다면 '수익률'이라는 단어가 있을 확률이 높음)