Brute Force(완전 탐색)

완전 탐색이란?

컴퓨터 과학에서 사용되는 알고리즘 중 하나이다. Brute Force는 무식한 힘 정도로 직독 직해 할 수 있는데, 이름에서 나타내는 것처럼 컴퓨터의 능력을 통해 특정 상황 시 경우에 수가 있다면 모든 경우의 수를 무차별 대입하면서 전부 탐색하는 방법이다.

이렇게 비밀번호를 6자리를 찾는다면 0부터 9까지 모든 자리를 대입하면서 찾는 방식이 완전 탐색이라고 한다. 이렇게 무식한 방식을 사용하면서 발생하는 특징은 다음과 같다.

특징

• 반드시 답을 찾을 수 있다.
• 답이 없더라도 답이 존재하지 않는다는 사실을 얻을 수 있음
• 오래걸리는 단점이 있다.
• 컴퓨팅 자원과 시간에 대하여 trade-off 관계이다.
  컴퓨팅 자원 <-> 시간

시간 복잡도 (Time complexity)

Average	Worst
$O(2^N)$	$O(2^N)$

Python에서의 Brute Force 예시

def find_pairs(N, M):
    count = 0
    for i in range(1, N + 1):
        for j in range(i + 1, N + 1):
            if i + j == M:
                count += 1
    return count


N = int(input())
M = int(input())
result = find_pairs(N, M)
print("총 경우의 수:", result)

해당 예시를 간단히 살피면 다음과 같다.

• N과 M을 입력받는다.
• N은 1~N까지의 수이다.
• M은 1~N까지 중 2개의 조합으로 나타내야 할 숫자다. ($N \leq M$)
• 가능한 경우의 수 출력

이처럼 Brute Force를 사용할 수 있다.

Brute Force 적용이 안되는 경우

N개의 수를 입력 받아서 두 수의 합이 가장 큰 경우를 나타내라.

위와 같은 문제가 있을 때 Brute Force를 통해 모든 경우의 수를 가지고 나타낼 수 있습니다.
$_NC_2$로 문제를 풀 수 있지만 만약 문제가 다음과 같다면 문제가 있을 수 있습니다.

N개의 수를 입력 받아서 두 수의 합이 가장 큰 경우를 나타내라.
$(2\leq N \leq 1,000,000)$ | 시간제한: 1초

이 경우 $_NC_2$를 최악에 경우로 계산하면 엄청 큰 값이 나타난다. $N * (N-1) / 2$ 이 경우 $O(N^2)$로 시간복잡도가 나타나며 문제는 브루트포스로 해결할 수 없다는 것을 알 수 있다.

방법

위와 같은 문제를 정렬이 된 배열로 해결한다면 어떻게 될까?
이 경우 가장 큰 수가 최상단에 존재하기 때문에 $O(log_2N)$으로 해결할 수 있게된다.

Python에서의 Brute Force 예시 2

완전 탐색 문제를 풀 때 용이한 경우가 잦은 순열과 조합에 대하여 파이썬에서 제공하는 모듈도 있다.

from itertools import permutations
from itertools import combinations

v = [0, 1, 2, 3]

for i in permutations(v, 2):
    print(i)

print("----")

for i in combinations(v, 2):
    print(i)

위 결과를 출력하면 다음과 같이 나타난다.

순열
(0, 1) (0, 2) (0, 3) (1, 0) (1, 2) (1, 3)
(2, 0) (2, 1) (2, 3) (3, 0) (3, 1) (3, 2)

---

조합
(0, 1) (0, 2) (0, 3) (1, 2) (1, 3) (2, 3)

위를 활용하여 문제를 풀 수도 있다.

Brute Force에 사용 예시

• 조합과 순열
• 비트 조합
• 패스워드 크래킹
• TSP (Traveling Salesman Problem)

정리

• 무식하게 모든 경우의 수를 봐도 시간 문제가 없을 지 확인하자
• 문제가 있다면 다른 알고리즘을 활용하도록 하자

---

Greedy algorithm(탐욕법)

탐욕법이란?

탐욕법은 최적의 해를 구하기 위해서 각 단계에서 가장 좋아보이는 해를 선택하는 알고리즘 기법이다.

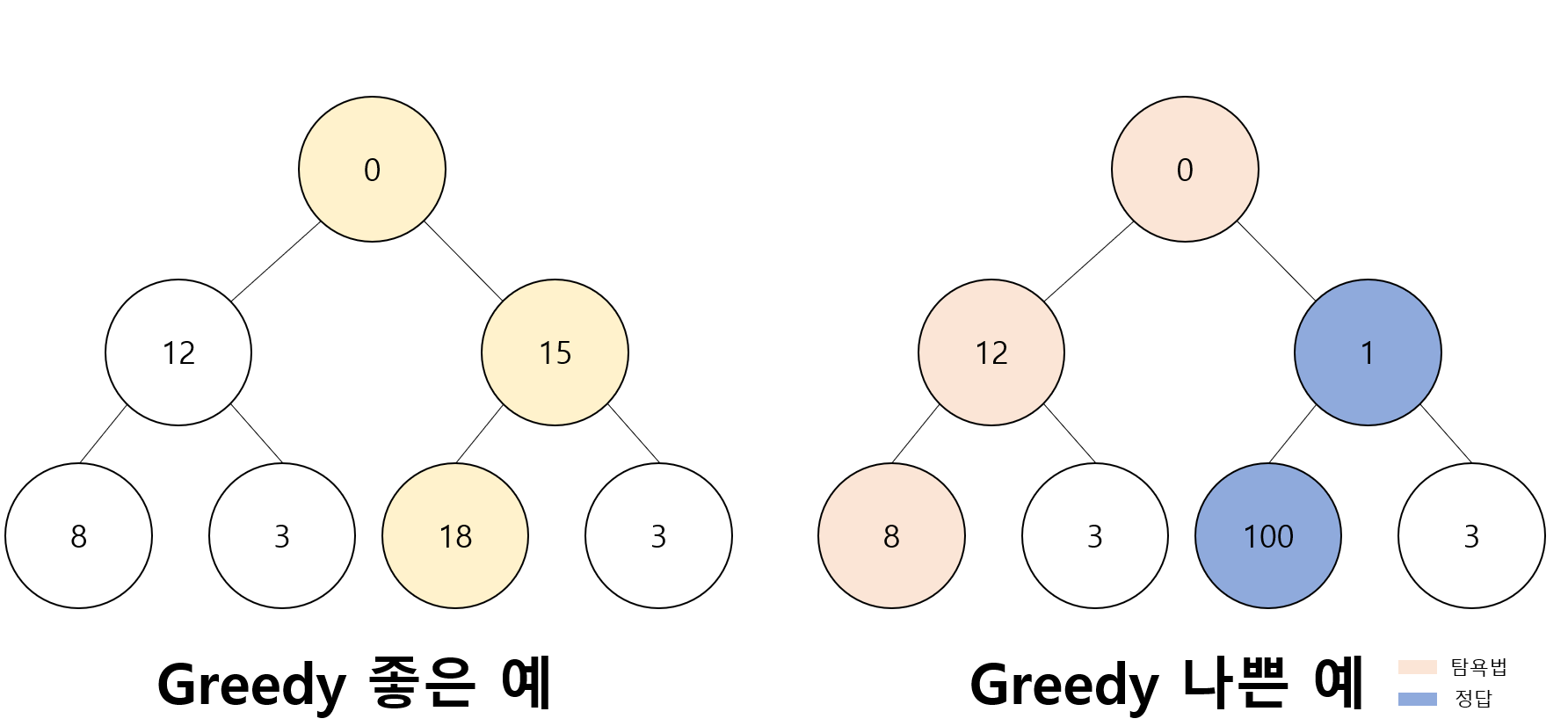
위 예시는 두 수의 합이 큰 값을 고르는 것으로 그리디는 각 단계에서 가장 큰 수로 접근하여 문제를 해결할 수 있는 예시입니다.

특징

• 각 단계에서의 선택은 그 순간에서 가장 최적인 선택이지만, 전체적으로 최적해를 보장하지는 않는다.
• 탐욕법은 간단하고 직관적인 방식
• 일반적으로 계산 비용이 적고 실행 시간이 빠르다.
• 많은 문제에 대해 유용한 접근법이지만, 항상 적용할 수 없다.
• 문제의 특성과 조건을 분석하여 최적해를 보장하는지 검토 (핵심 ❗)

시간 복잡도 (Time complexity)

Average	Worst
$O(Nlog_2N)$ or $O(N)$	$O(N^2)$

Python에서의 Greedy algorithm 예시

def coin_change(n, coins):
    coins.sort(reverse=True)
    result = []
    for coin in coins:
        while n >= coin:
            result.append(coin)
            n -= coin
    return result


N = int(input())
print(coin_change(N, [10, 50, 100, 500]))

동전 거슬러 주는 문제 예시

탐욕법의 사용 예시

• 거스름돈 주기
• 스케줄링
• 일부 탐색 문제
• 캐시 관리
• 다익스트라 알고리즘 (Dijkstra's Algorithm)
• 최소 스패닝 트리 알고리즘 (Minimum Spanning Tree Algorithm)
• Kruskal 알고리즘
• Prim 알고리즘