머신러닝 완벽가이드 4강

1 분류(Classification)의 개요

지도 학습은 레이블(Label), 즉 명시적인 정답이 있는 데이터가 주어진 상태에서 학습하는 머신러닝 방식이다. 지도학습의 대표적인 유형인 분류 학습 데이터로 주어진 데이터의 피처와 레이블값(결정 값, 클래스 값)을 머신러닝 알고리즘으로 학습해 모델을 생성하고, 이렇게 생성된 모델에 새로운 데이터 값이 주어졌을 때 미지의 레이블 값을 예측하는 것이다.

분류는 다양한 머신러닝 알고리즘으로 구현 가능하다.

예를들어, 로지스틱 회귀, 나이브 베이즈, 결정트리, 서포트 벡터 머신(SVM), 최소 근접 알고리즘, 심층 연결 기반의 신경망, 앙상블 등이 있다.

이번에는 다양한 알고리즘 중 앙상블 방법을 집중적으로 다룬다.

앙상블은 배깅과 부스팅으로 나뉜다. 배깅 방식의 대표인 랜덤 포레스트는 뛰어난 예측성능, 상대적으로 빠른 수행시간, 유연성 등으로 많은 분석가가 애용하는 알고리즘이다. 부스팅의 그래디언트 부스팅의 경우 뛰어난 예측 성능을 가지고 있지만, 수행 시간이 너무 오래 걸리는 단점으로 이해 최적화 모델 튜닝이 어려웠다. 하지만 Xgboost 와 LightGBM 등 기존 그래디언트 부스팅의 예측 성능을 한 단계 발전시키면서도 수행 시간을 단축시킨 알고리즘이 계속 등장하면서 정형 데이터 분류 영역에서 가장 활용도가 높은 알고리즘으로 자리잡았다.

앙상블은 서로 다른 / 또는 같은 알고리즘을 결합한다. 앙상블의 기본 알고리즘으로 일반적으로 사용하는 것은 결정 트리이다.

결정트리는 쉽고 데이터의 스케일링이나 정규화 등의 사전 가공 영향이 매우 적지만, 예측 성능을 향상시키기 위해 복잡한 규칙 구조를 가지고 있고, 이로 인해 과적합이 발생해 예측 성능 저하를 일으킬수도있다. 그러나 앙상블은 매우 많은 약한 학습기(즉, 예측 성능이 상대적으로 떨어지는 학습 알고리즘)를 결합해 확률적 보완과 오류가 발생한 부분에 대한 가중치를 계속 업데이트하면서 예측 성능을 향상시키는데 결정 트리가 좋은 약한 학습기가 되기도한다.

2 결정트리

결정트리는 데이터에 있는 규칙을 학습을 통해 자동으로 찾아내 트리 기반의 분류 규칙을 만드는 것이다. 규칙을 가장 쉽게 표현하면 if/else 기반으로 나타내는 것이다.

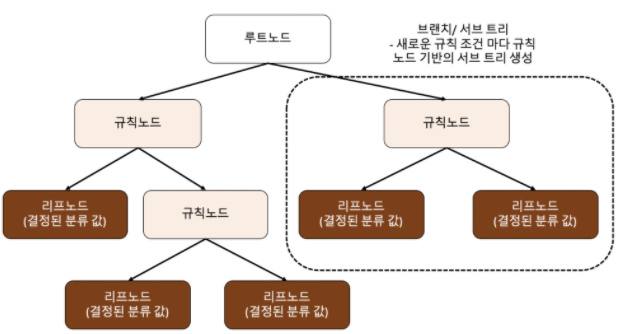
규칙 노드로 표시된 노트는 규칙 조건이 되는 것이고, 리프 노드는 결정된 클래스 값이다. 새로운 규칙 조건마다 서브트리가 생성된다. 데이터 세트에 피처가 있고 이러한 피처가 결합해 규칙 조건을 만들 때마다 규칙 노드가 만들어진다. 하지만 많은 규칙이 있다는 것은 곧 과적합으로 이어질 수 있다. 따라서 트리의 깊이(depth)가 깊어질수록 트리 예측 성능이 떨어질수 있다.

가능한 한 적은 결정 노드로 높은 예측 정확도를 가지려면 데이터를 분류할 때 최대한 많은 데이터 세트가 해당 분류에 속할 수 있도록 결정 노드의 규칙이 정해져야한다. 이를 위해서는 어떻게 트리를 분할 할 것인지도 중요한데, 최대한 균일한 데이터 세트를 구성할 수 있도록 분할하는 것이 중요하다.

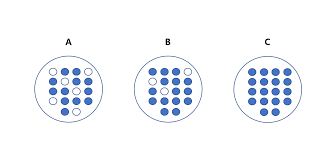
균일한 데이터 세트순으로 순서를 나타내보자면, C > B > A이다. C의 경우 모두 파란 공으로 이루어져있어 가장 균일 한 것이다. 상대적으로 A의 경우 혼잡도가 높고 균일도가 낮기 떄문에 같은 조건에서 데이터를 판단하는 데 있어 더 많은 정보가 필요하다.

정보의 균일도를 측정하는 대표적인 방법은 엔트로피를 이용한 정보 이득 (Information Gain)지수와 지니 계수가 있다.

• 정보 이득은 엔트로피라는 개념을 기반으로 한다. 엔트로피는 주어진 데이터 집합의 혼잡도를 의미하는데, 서로 다른 값이 섞여 있으면 엔트로피가 높고, 같은 값이 섞여 있으면 엔트로피가 낮다. 정보 이득 지수는 1에서 엔트로피 지수를 뺀 값으로, 1- 엔트로피 지수이다. 결정 트리는 이 정보 이득 지수로 분할 기준을 정한다. ( 즉, 정보이득 지수 = 1- 엔트로피 지수(엔트로피는 균일도와 반비례) )

• 지니 계수는 불평등 지수를 나타낼 때 사용하는 계수이다. 0이 가장 평등하고 1 이 가장 불평등하다. 머신러닝에 적용할때는 지니 계수가 낮을수록 데이터 균일도가 높은 것으로 해석해 지니 계수가 낮은 속성을 기준으로 분할한다.

2-1 결정트리 모델의 특징