Sort
퀵 정렬 (Quick Sort 정렬)
정렬하는 방법에는 여러가지가 있다.
선택, 버블, 삽입, 셸, 합병 등~
그 중 퀵은 다른 알고리즘에 비해 자료들을 서로 비교하고 교환하는 횟수가 적다는 장점이 있다. (이는 수향 시간 단축으로 이어진다.) ⇒ 대용량 데이터베이스 처리 시스템 등 이용!
Quick Sort
무작위의 수가 있다고 가정하면, 4개의 레이블이 있어야한다.
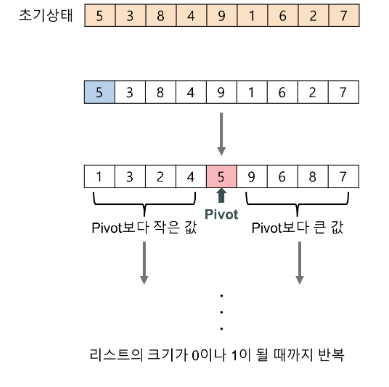
퀵 정렬 알고리즘 개념 요약
퀵 정렬은 불안정 정렬이며, 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬에 속한다.
분할 정복 알고리즘의 하나로, 평균적으로 매우 빠른 수행 속도를 자랑하는 정렬 방법이다. (Merge sort = 합병 정렬)과 달리 퀵 정렬은 리스트를 비균등하게 분할한다.
분할 정복 방법
문제를 작은 2개의 문제로 분리하고 문제를 작은 2개의 문제로 분리하고 해결한다음, 결과를 모아서 원래의 문제를 해결하는 방식이다.
분할 정복방법은 대개 순환 호출을 이용하여 구현한다.
과정 설명
- 리스트 안에 있는 한 요소 선택한다. (이것을 피벗이라고 한다.)
- 피벗을 기준으로 작은것은 모두 왼쪽으로, 큰 것은 모두 오른쪽으로 이동시킨다.
- 피벗을 제외한 왼쪽리스트, 오른쪽 리스트를 다시 정렬한다.
- 분할된 부분 리스트에 대해 순환 호출을 이용해 정렬을 반복한다.
- 부분 리스트에서도 다시 피벗을 정하고 기준으로 2개의 부분 리스트로 나누는 과정을 반복한다.
- 부분 리스트들이 더이상 분할이 불가능할때까지 반복!
- 리스트의 크기가 0 이나 1이 될때까지 반복한다!
퀵 정렬 알고리즘 구체적인 개념!
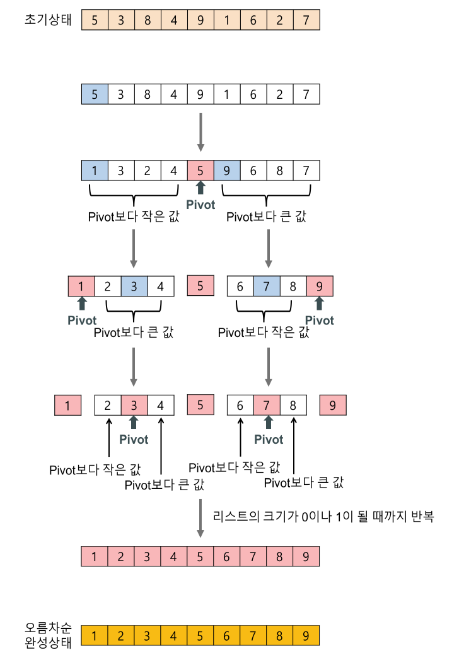
하나의 리스트를 피벗 기준으로
퀵 정렬은 3가지 단계로 이뤄진다.
- 분할
- 입력 배열을 피벗 기준으로 비균등하게 2개의 부분 배열로 분할한다.(피벗기준으로 왼, 오른쪽으로!)
- 정복
- 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용해 다시 분할 정복 방법을 적용한다. (다시 1번(분할)으로)
- 결합
- 정렬된 부분 배열들을 하나의 배열에 합병한다.
- 순환 호출이 한번 진행될 때마다 최소한 하나의 피벗은 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.
quick sort 알고리즘의 특징
-
장점
- 속도가 빠르다. 시간 복잡도 O(nlog2n) 를 가지는 다른 정렬 알고리즘과 비교해도 가장 빠르다.
- 추가 메모리 공간을 필요로 하지 않는다. 퀵정렬은 O(log n) 만큼의 메모리를 핑요로 한다.
-
단점
- 정렬된 리스트에 대해서는 퀵정렬의 불균형 분할에 의해 오히려 수행 시간이 더 많이 걸린다.
- 퀵정렬의 불균형 분할을 방지하기 위해 피벗을 선택할때 더욱 리스트를 균등하게 분할할 수 있는 데이터를 선택한다.
- ex ) 리스트 내의 몇 개의 데이터 중에서 크기순으로 중간 값을 피벗으로 선택한다.
시간 복잡도
와 지금은 봐도 모르겠다…
최선의 경우
T(n) = O(nlog2n)
- 비교횟수
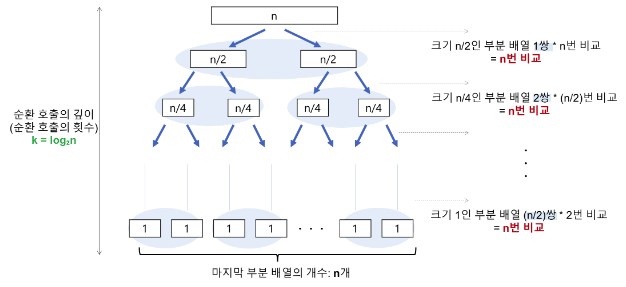
- 순환 호출의 깊이 레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, n=2^3의 경우, 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있다. 이것을 일반화하면 n=2^k의 경우, k(k=log₂n)임을 알 수 있다.
k=log₂n
- 각 순환 호출 단계의 비교 연산 각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다.
평균 n번 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = nlog₂n
- 이동 횟수
- 비교 횟수보다 적으므로 무시할 수 없다.
최악의 경우
리스트가 계속 불균형하게 나눠지는 경우 (이미, 정렬된 리스트에 대해 퀵 정렬을 실행하는 경우!)
- 비교 횟수
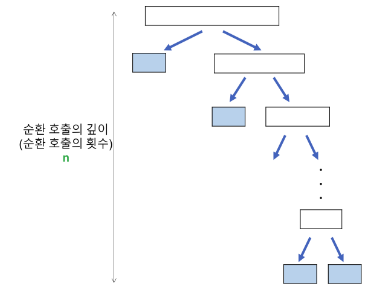
- 순환 호출의 깊이
- 레코드의 개수 n 이 2의 거듭 제곱이라고 가정 했을때, 순환호출의 깊이는 n임을 알 수 있다.
- n
- 각 순환 호출 단계의 비교 연산
- 이동 횟수
- 평균 평균 T(n) = O(nlog₂n)
시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
퀵 정렬이 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환할 뿐만 아니라, 한 번 결정된 피벗들이 추후 연산에서 제외되는 특성 때문이다.
정렬 알고리즘 시간복잡도 비교
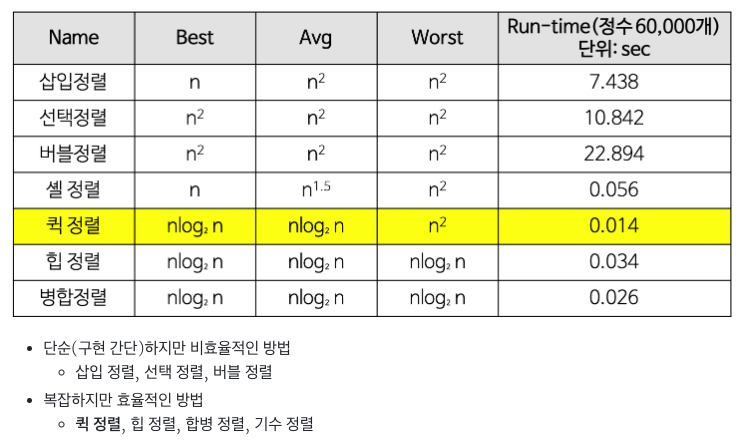
출처 : https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html
