Pose Estimation / Triangulation / Reconstruction
컴퓨터 비전에서 추정을 한다고 하면 3가지가 있다. 이 3개는 주어진 것, 알아내고자 하는 것이 각자 다르다.
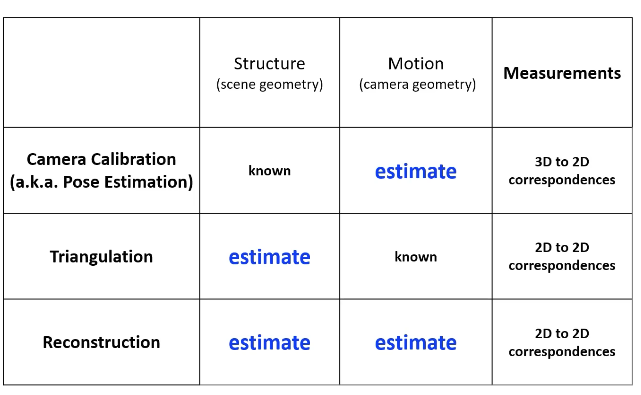
- camera calibration: 3차원 좌표를 2차원 이미지로 정확하게 매핑하기 위해 사용된다. 카메라의 모션(움직임)을 추정하기 위해 사용된다. 여러 이미지에서 동일한 3차원 포인트를 관찰하려 카메라의 위치 변화와 회전을 계산할 수 있다.
- triangulation: 두 개의 다른 카메라 뷰에서 얻은 정보를 바탕으로 3차원 좌표를 추정한다. 두 개의 카메라 뷰에서 동일한 2차원 포인트를 관찰한 경우에 카메라의 기하학적 관계를 이용해서 포인트의 3차원 좌표를 계산할 수 있다.
- reconstruction: 다수의 view에서 얻은 정보를 바탕으로 3차원 장면을 재구성한다. AR같은 응용 프로그램에서 사용된다.
Triangulation
- given: camera matrix, noisy matched points
- estimate: 3차원 좌표

카메라 matrix, 좌표 모두 error가 있을 수 있고, noise 때문에 그림처럼 두 선이 만날 확률이 매우 적다.
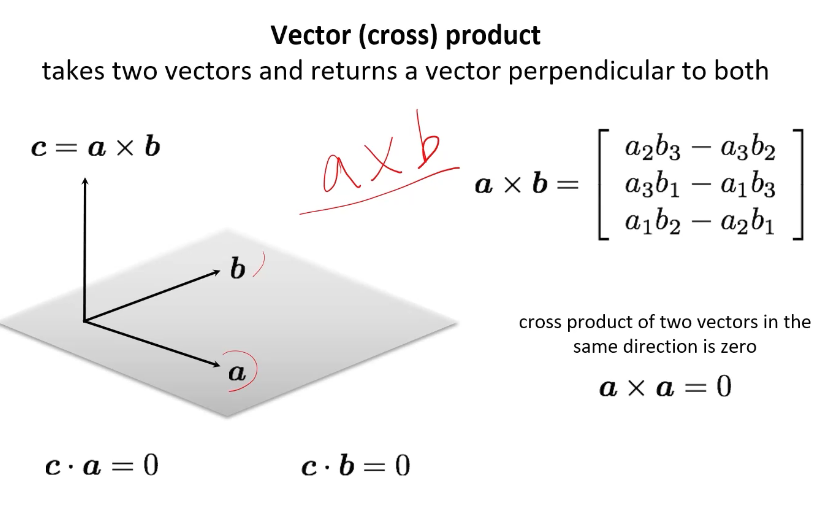
Recall: Cross Product
벡터의 외적.
triangulation formation

1. 교차곱은 0이 되어야 한다
- 2차원 이미지의 점과 3차원 공간의 점간 관계는 선형 방정식으로 표현된다. 만약 모든 점이 동일한 곳에 있다면, 이 점들을 연결하는 벡터간 교차곱은 0이 된다. 이를 이용하여 3차원 좌표를 추정할 수 있다.
- 3번째 선은 1번째 선과 2번째 선의 선형 결합이다.
- 3개의 선이 주어졌을 때 3번째 선이 나머지 두 선의 선형 결합으로 표현될 수 있다면, 이는 세 선이 모두 동일한 평면 위에 있음을 나타낸다.
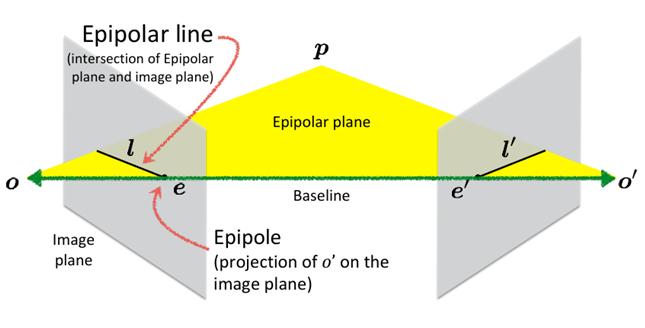
Epipolar Geometry
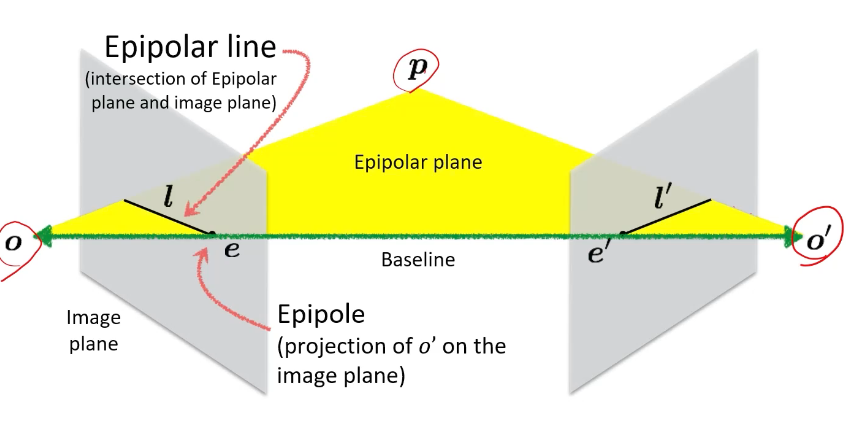
- given: 두 카메라의 센터, 어떤 점 P
- epipolar plane: centers, p를 지나는 평면
- baseline: 두 원점 사이의 벡터
- epipole: 왼쪽 이미지의 epipole은 오른쪽 center의 projection
- epipolar line: epipolar plane과 plane이 만나는 선
Epipolar Constraint
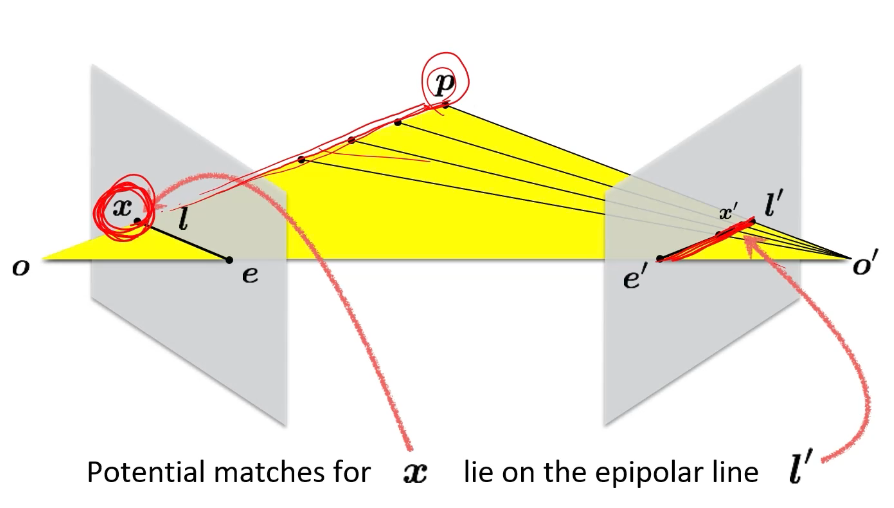
카메라1, 카메라2로 하나의 점을 촬영했을 때, 카메라1에서 본 점의 위치는 카메라2의 이미지 평면에서 epipolar line 위에 투영된다. epipolar constraint의 핵심은 한 카메라에서 관측된 특정 점에 대응하는 점이 다른 카메라의 이미지에서 찾아질 수 있는 위치가 epipolar line에 의해 제한된다는 것이다.
Converging Cameras

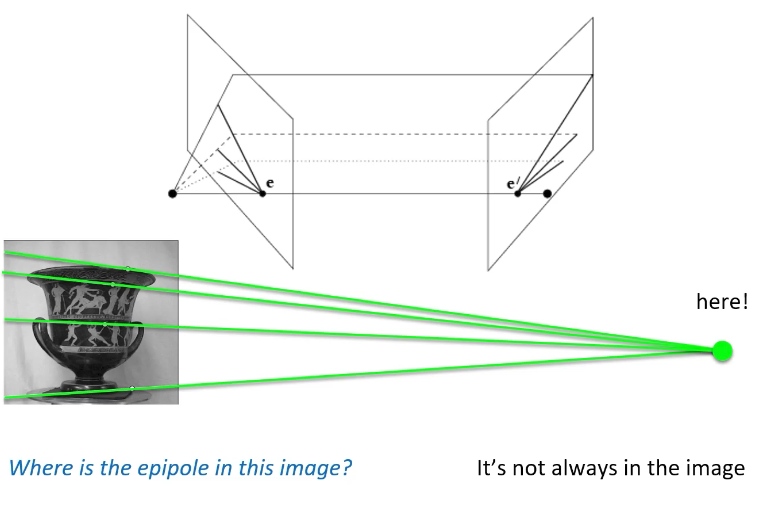
두 대의 카메라가 비슷한 시점에서 약간 다른 각도로 같은 장면을 촬영하여, 두 이미지 간의 차이를 이용해 깊이 정보를 추출한다. 카메라가 서로를 향해 경사져 있는 경우 converging 상태이다.
Parallel Cameras
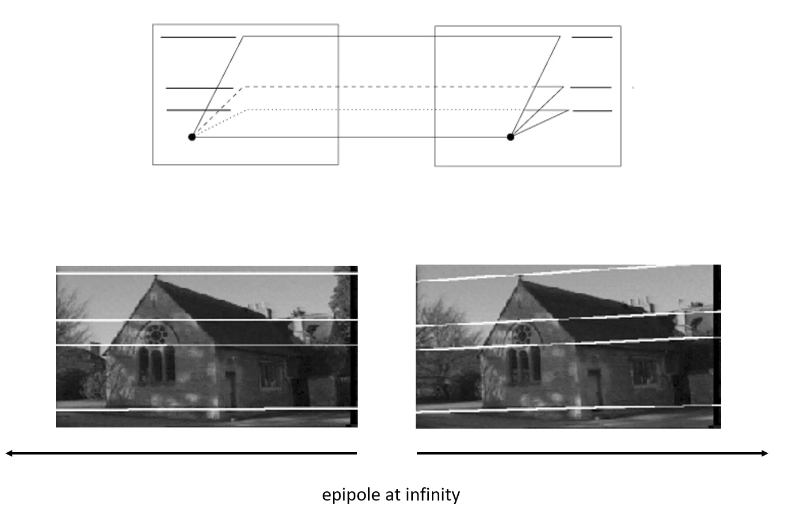
두 대의 카메라가 서로 평행하게 배치되어 동일한 방향을 향하는 경우, epipole이 무한대에 위치하게 된다. epipole은 두 카메라의 광축이 교차하는 지점인데, parallel cameras의 경우 광축이 교차하지 않기 때문에 무한대에 위치하게 된다. 이때 epipolar line은 수평선으로 나타난다.
Forward Moving Camera
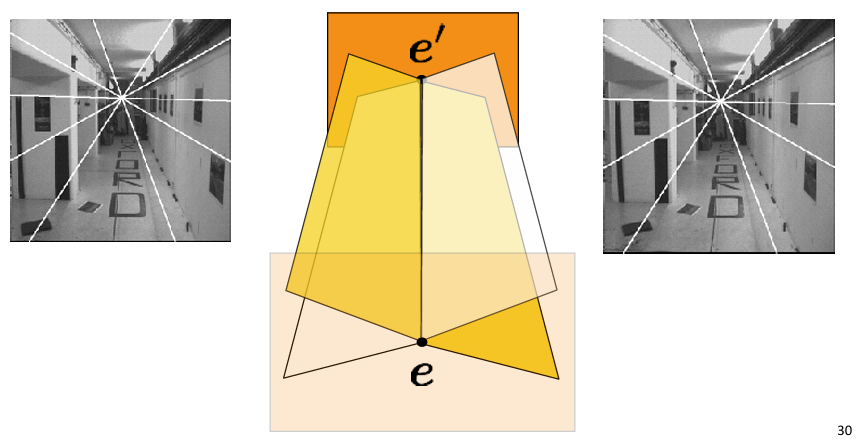
카메라가 전진하는 경우 epipole은 이미지 평면에서 동일한 좌표를 가진다. 이는 카메라의 이동 방향이 이미지 평면에 수직이기 때문이다. 모든 이미지 포인트는 FOE로부터 방사형으로 퍼져나가는 선을 따라 이동한다.
The Essential Matrix
From Epipolar Constraint
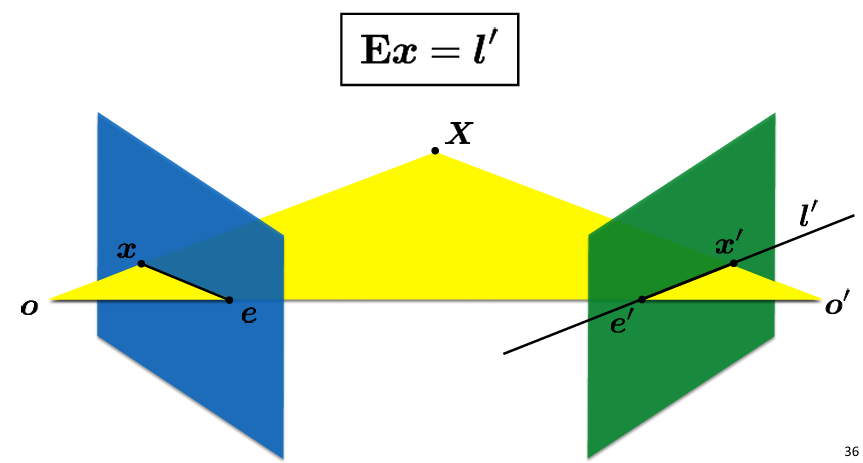
한 이미지 내의 점을 주어진 essential matrix를 곱함으로써 두 번째 시점의 epipolar line을 구할 수 있다. 여기서 essential matrix는 3x3 행렬이다.
한 이미지에서의 점 x와 에센셜 행렬 E를 사용하여 두 번째 이미지에서의 epipolar line I'을 찾는 공식은 Ex = I'이다.
Essential Matrix
- x: 첫 번째 이미지의 한 점을 나타내는 동차 좌표
- I: x에 대응하는 두 번째 이미지에서의 epipolar line
- E: Essential matrix
- x.T * I = 0: 점x가 epipolar line 위에 있지 않다면, 두 벡터는 직교한다.
- Ex = I': 첫 번째 이미지의 점x와 두 번째 이미지의 epipolar line I' 사이의 관계
따라서 x'.T * Ex = 0은 epipolar constraint를 나타낸다.
Derivation of the Essential Matrix
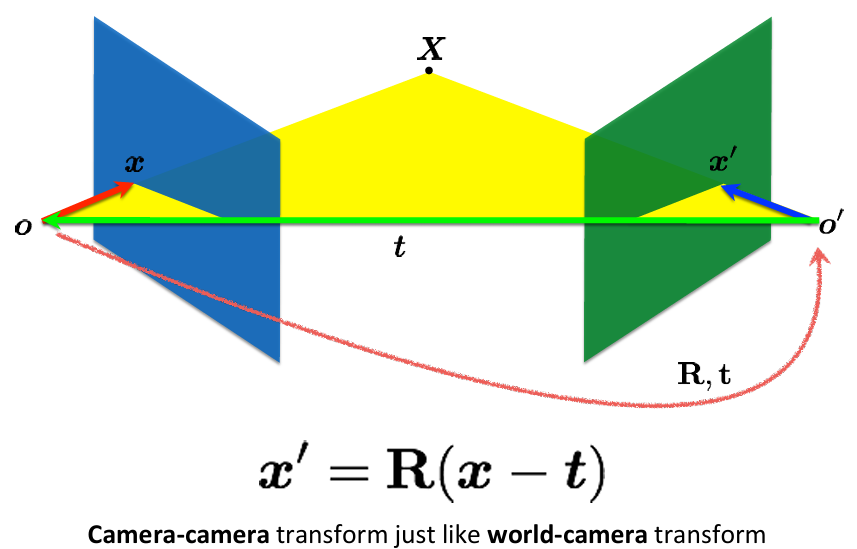
두 카메라의 관계를 설명하기 위해 회전행렬 R과 변환벡터 t를 사용한다. 한 카메라 좌표계에서 다른 카메라 좌표계로 변환하기 위해 x' = R(x-t)라는 관계식을 사용한다.
- x: 첫 번째 이미지의 한 점의 좌표
- x': 두 번째 이미지의 대응점
- R: 회전행렬
- t: 변환벡터

- 두 카메라 좌표계 간의 관계 정립: x' = R(x - t)
- 외적 행렬 t 도입
- 두 점 사이의 관계식: x'(R x - t) = 0
- 본질 행렬 정의: E = tR
- 에피폴라 제약식: x'.T * Ex = 0
Essential Matrix and Fundamental Matrix
image coordinate에 사용한다.

기본 행렬 (Fundamental Matrix)를 분해하는 과정은 F가 내부 파라미터, 외부 파라미터 모두에 의존한다는 점을 고려해야 한다. F는 두 카메라 뷰 사이의 픽셀 좌표 관계를 나타내는 3x3 행렬이다. F를 분해하여 카메라의 위치, 내부 파라미터를 추정하는 과정은 여러 단계로 구성된다.
1. F 계산: 대응되는 점들의 집합을 사용하여 F를 계산한다.
2. 기본 행렬 F의 분해: F를 분해하여 E를 얻는다. E = K'.T * FK. 여기서 K와 K'은 첫 번째, 두 번째 카메라의 내부 파라미터 행렬이다.
3. E의 분해: E를 분해하여 R과 t를 얻는다. E = UDV.T
Eight Point Algorithm
eight point algorithm은 정합된 이미지 포인트들에 기반하여 기본 행렬 F를 계산하는 방법이다. M개의 정합된 이미지 포인트가 있다고 가정할 때, 각 정합은 x'.T * Fx = 0를 만족해야 한다. F는 3x3 크기의 기본 행렬이다.
1. (정규화): 이미지 포인트의 정확도를 높이기 위함.
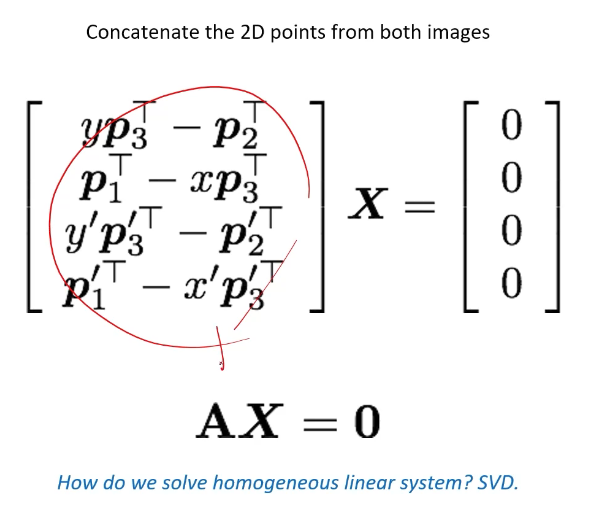
2. linear system 구성: 각 포인트 쌍에 대해 (x'x, x'y, x', y'x, y'y, y', x, y, 1) 형태의 방정식을 구성한다. M개의 포인트 쌍을 가지고 있으면 Mx9 크기의 행렬 A를 구성할 수 있다.
3. SVD 사용: 행렬 A에 대해 SVD를 적용하여 F를 구한다. SVD는 A를 UDV.T 형태로 분해한다. F행렬은 V의 마지막 열에 해당한다.
4. (F 행렬의 rank 조정): F의 rank는 2여야한다. SVD를 통해 계산된 F는 이 조건을 만족하지 못할 수 있다. 이를 해결하기 위해 F에 대해 다시 SVD를 수행하고, 가장 작은 특이값을 0으로 설정한 후 다시 F 행렬을 계산한다.
5. (Denormalization): 정규화된 포인트를 다시 원래 좌표계로 변환
epipolar constraint에 따라 각 점들의 쌍은 하나의 스칼라 방정식만 제공한다. 이는 homography 추정과 다른 점이며, homography 추정에서는 각 점들의 쌍이 2개의 방정식을 제공한다.
normalized eight-point algorithm
- 이미지 데이터 정규화
- 각 이미지에 대해 모든 data points를 원점 중심으로 이동시킨다. 모든 포인트들의 평균이 (0,0)이 되도록 한다.
- 데이터 포인트들과 우너점 사이의 평균 제곱 거리가 2 픽셀이 되도록 스케일을 조정한다. -> 모든 포인트들이 원점으로부터 대체로 동일한 거리에 위치하도록 만들어준다.
- 정규화된 포인트들로 F 계산
- Rank 2 제약 조건 적용
- F에 대해 SVD를 적용하고, 가장 작은 특이값을 0으로 만들어 rank를 2로 조정한다.
- 원래 단위로 F 변환
- T, T'가 있을 때 원래 좌표계로의 변환은 T'.T * FT로 계산된다.
Enforcing Rank Constraints
주어진 행렬 F와 가장 가까운 순위를 가진 행렬 F'를 찾아야 한다.
1. SVD 계산
- 행렬 F에 대해 SVD를 수행하여 F = U Sigma V.T 형태로 분해한다. U와 V는 직교 행렬, sigma는 대각선 원소가 특이값이고 나머지 원소는 모두 0인 대각행렬이다.
- Sigma의 수정
- sigma 행렬에서 가장 큰 k개의 특이값을 제외한 모든 특이값을 0으로 대체한다. rank가 k인 행렬이 된다.
- F' 계산
- 수정된 sigma'를 사용하여 F' = U Sigma' V.T를 계산한다.
Nonlinear Estimation
에피폴라 기하학에서 발생하는 거리를 최소화하는 방식은 크게 2가지가 있다.
1. linear estimation
- 두 점 사이의 거리의 제곱합을 최소화
- 기하학적 의미에서 최솟값이 아닐 수 있다.
- nonlinear approach
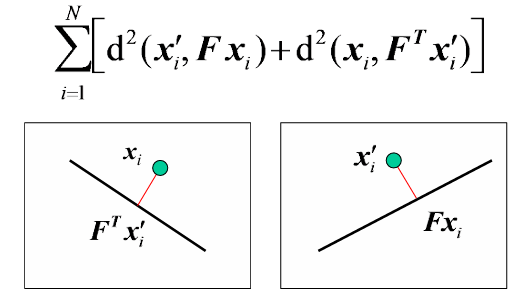
- epipolar line과 대응되는 점 사이의 기하학적 거리의 제곱합을 최소화
- 더 정확하지만, 계산 복잡도가 높고, 초기 추정값의 중요성이 더 크다.
Experimental Comparison of Estimation Algoritms

From Epipolar Geometry to Camera Calibration
- Fundamental Matrix를 추정하는 것은 weak calibration이라고 한다.
- 두 카메라의 calibration matrices를 알고 있으면, essential matrix를 추정할 수 있다. essential matrix는 카메라의 상대적 회전, 평행이동, 외부 파라미터들을 제공한다. 이를 통해 두 카메라 간의 3D 변환을 추정할 수 있다.
- Five Point Algoritm: calibration matrix를 알고 있는 경우, five point algorithm을 사용할 수 있다. 두 이미지에서 5개의 대응점을 찾고, essential matrix를 추정할 수 있다. E를 SVD 분해하여 회전, 평행이동을 추출할 수 있다.
