Greedy(탐욕) 알고리즘은 현재 상황에서 가장 좋아 보이는 선택을 반복하며 문제를 해결하는 알고리즘이다. 말 그대로 “눈앞의 이익을 최우선으로 하는 전략”을 사용한다.
즉, 매 순간 최적이라고 생각되는 선택을 하고 이 선택들이 쌓여서 결국 전역 최적해(Global Optimum)에 도달하길 기대하는 방식이다. 특징은 한 번 내린 선택을 다시 바꾸지 않는다는 것이다.
장점
- 구현이 쉽고 빠르다 (
O(N log N)~O(N)) - 직관적이며 실전 코딩 테스트에서 자주 등장
단점
- 항상 최적해를 보장하지 않는다
- 문제의 특성을 잘못 이해하면 오답 발생
대표 문제
| 문제 유형 | 문제 설명 | 탐욕 전략 | 예시 |
|---|---|---|---|
| 동전 거스름돈 | 최소 개수의 동전으로 거스름돈 지급 | 가장 큰 동전부터 선택 | 500, 100, 50, 10원으로 1260원 거슬러주기 |
| 활동 선택(Activity Selection) | 겹치지 않게 최대한 많은 활동 선택 | 종료 시간이 빠른 순으로 선택 | (1,4), (3,5), (0,6) 등 |
| 회의실 배정 | 최대한 많은 회의 배정 | 종료 시간 빠른 순으로 회의 선택 | 시작/종료 시간 주어짐 |
| 최소 스패닝 트리(MST) | 그래프의 최소 연결 비용 | Kruskal: 가중치 낮은 간선부터 선택 | Union-Find와 함께 사용 |
| 허프만 코딩(Huffman Coding) | 최소 길이의 이진 코드 생성 | 빈도 낮은 노드부터 병합 | 텍스트 압축에 활용 |
| 다익스트라(Dijkstra) | 가중치 양수인 최단 경로 | 현재까지 가장 가까운 노드부터 확정 | BFS + 우선순위 큐 활용 |
| Prim 알고리즘 | MST 생성 | 가장 가중치 작은 간선부터 확장 | 다익스트라와 유사 구조 |
| 배낭 문제(Knapsack, Fractional) | 담을 수 있는 최대 가치 계산 | 단위 가치(가치/무게) 높은 순으로 담기 | 0/1 배낭 문제에는 적용 불가 |
| Job Scheduling | 마감 기한과 이익이 있는 작업 스케줄링 | 이익이 큰 작업부터 가능한 가장 늦은 시간에 배치 | CPU 스케줄링 문제와 유사 |
적용 조건
Greedy 알고리즘이 항상 최적해를 보장하는 것은 아니다. 다음 조건을 만족할 때만 최적해를 구할 수 있다.
1. 탐욕 선택 속성(Greedy Choice Property)
각 단계에서의 최적 선택이 전체 문제의 최적해로 이어짐
2. 최적 부분 구조(Optimal Substructure)
문제의 최적해가 부분 문제의 최적해로 구성될 수 있음
예를 들어 동전 거스름돈 문제에서 동전 단위가 10, 50, 100원이라면 가장 큰 동전부터 거슬러주는 탐욕 전략이 항상 최적해를 만든다. 하지만 10원, 40원, 50원 동전이 있다면 탐욕적 접근은 항상 최적해를 보장하지 않는다.
대표 예제
1. 동전 거스름돈 문제
문제: 최소 개수의 동전으로 N원을 거슬러 주기
조건
- 동전 종류: 500, 100, 50, 10
- N = 1260원
탐욕 전략
1. 현재 남은 금액에서 가장 큰 동전 선택
2. 남은 금액이 0원이 될 때까지 반복
int[] coins = {500, 100, 50, 10};
int n = 1260;
int count = 0;
for (int coin : coins) {
count += n / coin; // 해당 동전으로 거슬러줄 개수
n %= coin; // 남은 금액
}
System.out.println(count); // 6실행 과정
1. 500원 → 2개 (남은 금액 260원)
2. 100원 → 2개 (남은 금액 60원)
3. 50원 → 1개 (남은 금액 10원)
4. 10원 → 1개 (남은 금액 0원)
총 6개의 동전으로 해결된다.
2. 활동 선택 문제(Activity Selection Problem)
문제: 겹치지 않게 최대한 많은 활동 선택하기
- 시작 시간과 종료 시간이 있는 활동 목록
- 종료 시간이 빠른 순으로 정렬 후 선택하면 최적해를 얻을 수 있음
class Activity {
int start, end;
Activity(int s, int e) { start = s; end = e; }
}
List<Activity> activities = List.of(
new Activity(1, 4),
new Activity(3, 5),
new Activity(0, 6),
new Activity(5, 7),
new Activity(8, 9),
new Activity(5, 9)
);
// 종료 시간 기준 정렬
activities = activities.stream()
.sorted(Comparator.comparingInt(a -> a.end))
.toList();
int count = 0;
int lastEnd = 0;
for (Activity a : activities) {
if (a.start >= lastEnd) {
count++;
lastEnd = a.end;
}
}
System.out.println(count); // 3이 문제에서는 겹치지 않는 최대한 많은 활동을 선택해야 한다. 여기서 탐욕 알고리즘을 적용할 수 있는 핵심 이유는 종료 시간이 빠른 활동을 먼저 선택하면 남은 시간에 더 많은 활동을 배치할 수 있기 때문이다. 동작 과정은 다음과 같다.
- 모든 활동을 종료 시간이 빠른 순으로 정렬한다.
- 현재 시점에서 가장 빨리 끝나는 활동을 선택한다.
- 마지막으로 선택한 활동의 종료 시간 이후에 시작하는 활동 중 가장 빨리 끝나는 활동을 선택한다.
- 위 과정을 반복하여 더 이상 선택할 수 있는 활동이 없을 때 종료한다.
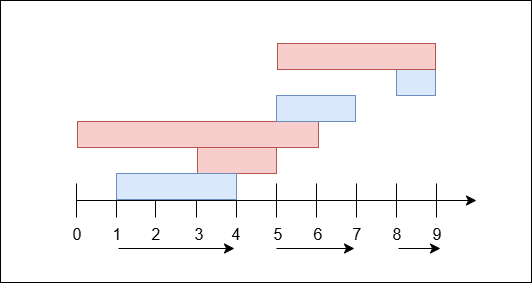
예시 입력
(1,4), (3,5), (0,6), (5,7), (8,9), (5,9)- 종료 시간으로 정렬
(1,4), (3,5), (0,6), (5,7), (5,9), (8,9)- 선택 과정
- 처음에는 종료 시간이 가장 빠른
(1,4)선택 → 마지막 종료 시각 4 - 다음으로 시작 시간이 4 이상인
(5,7)선택 → 마지막 종료 시각 7 - 마지막으로 시작 시간이 7 이상인
(8,9)선택 → 마지막 종료 시각 9 - 더 이상 선택할 수 있는 활동이 없음 → 종료
결과: 3개의 활동 선택
📝 느낀점
Greedy 알고리즘은 단순히 현재 상황에서 최적이라고 생각되는 선택을 반복하지만 모든 문제에서 정답을 보장하지는 않는다. 이번 활동 선택 문제는 종료 시간이 가장 빠른 활동을 고르는 탐욕 전략이 최적 부분 구조와 탐욕 선택 속성을 모두 만족하기 때문에 탐욕 알고리즘으로도 최적해를 얻을 수 있었다.
문제를 풀면서 깨달은 점은 탐욕 알고리즘을 적용할 수 있는 문제인지 먼저 판단하는 과정이 매우 중요하다는 것이다. 문제를 보면 곧바로 그리디를 적용할 수 있는지 확인하기 위해 아래를 점검해야 한다.
- 매 순간의 최적 선택이 전체 최적해로 이어질 수 있는가?
- 이전 선택을 나중에 바꿔야 할 필요가 없는가?
- 작은 문제의 최적해를 합치면 전체 최적해를 만들 수 있는 구조인가?
이 조건을 만족하면 탐욕 알고리즘으로 빠르게 해결할 수 있고 만약 그렇지 않다면 DP나 백트래킹 같은 다른 접근법을 고려해야 한다. 이번 예제를 통해 문제를 구조적으로 분석하고 탐욕 속성이 있는지 파악한 뒤 탐욕 알고리즘을 적용하는 것이 중요하다는 걸 다시 한 번 느꼈다.
