[Java / 알고리즘] 벨만-포드(Bellman-Ford) 이해하기

벨만-포드(Bellman-Ford) 알고리즘

출발점에서 목표점까지의 최단 경로를 구하는 알고리즘

• 음수 간선이 포함되어 있어도 최단 경로 구할 수 있음
  • 음수 싸이클이 있으면 정상 동작하지 않음
• 매번 모든 간선을 확인하기 때문에 다익스트라에 비해 느림
• 시간 복잡도 : O(VE)

다익스트라와 벨만-포드의 차이

다익스트라
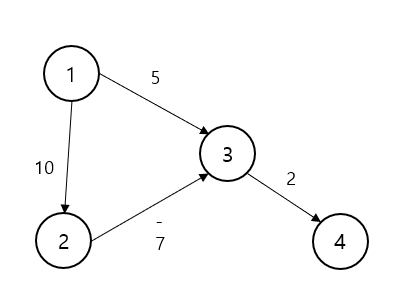
현재 노드에서 가장 인접한 노드로 진행
1. distance[2] = 10, distance[3] = 5 로 업데이트
2. distance[2] 와 distance[3] 비교시 distance[3]이 작기 때문에 distance[4] = 7로 업데이트
3. distance[2] -> distance[3] 가는 시간이 더 짧기 때문에 distance[3] = 3 업데이트 후 종료
🤔 음수 간선이 올 때 케이스에 따라 다익스트라론 올바른 값을 못 가져올 수 있기 때문에 음사 간선이 있을 땐 벨만-포드 알고리즘을 사용하자

벨만-포드
모든 경로를 다 돌리고 종료가 됨
1. distance[2] = 10, distance[3] = 5 로 업데이트
2. distance[4] = 7 로 업데이트
3. distance[2] 를 통해 distance[3]을 가는 시간이 짧기 때문에 distance[3] = 3 으로 업데이트
4. distance[4] = 5 로 업데이트하고 종료

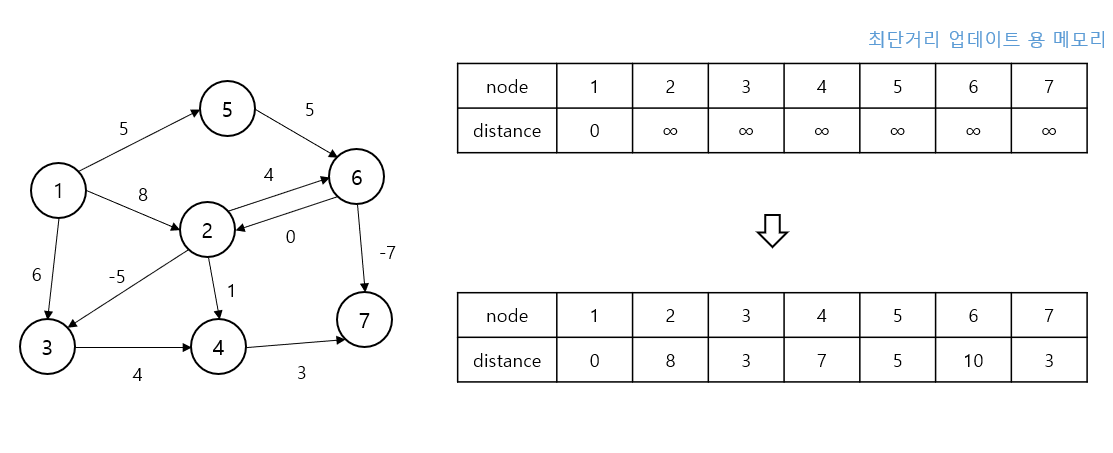
동작 방식

1. 1 노드에서 distance[2] = 8, distance[3] = 6, distance[5] = 5 업데이트
   • distance = {0, 8, 6, INF, 5, INF, INF}
2. 2 노드에서 distance[3] = 3, distance[4] = 9, distance[6] = 12 업데이트
   • distance = {0, 8, 3, 9, 5, 12, INF}
3. 3 노드에서 distance[4] = 7 업데이트
   • distance = {0, 8, 3, 7, 5, 12, INF}
4. 4 노드에서 distance[7] = 10 업데이트
   • distance = {0, 8, 3, 7, 5, 12, 10}
5. 5 노드에서 distance[6] = 10 업데이트
   • distance = {0, 8, 3, 7, 5, 10, 10}
6. 6 노드에서 distance[7] = 3 업데이트 후 종료
   • distance = {0, 8, 3, 7, 5, 10, 3}

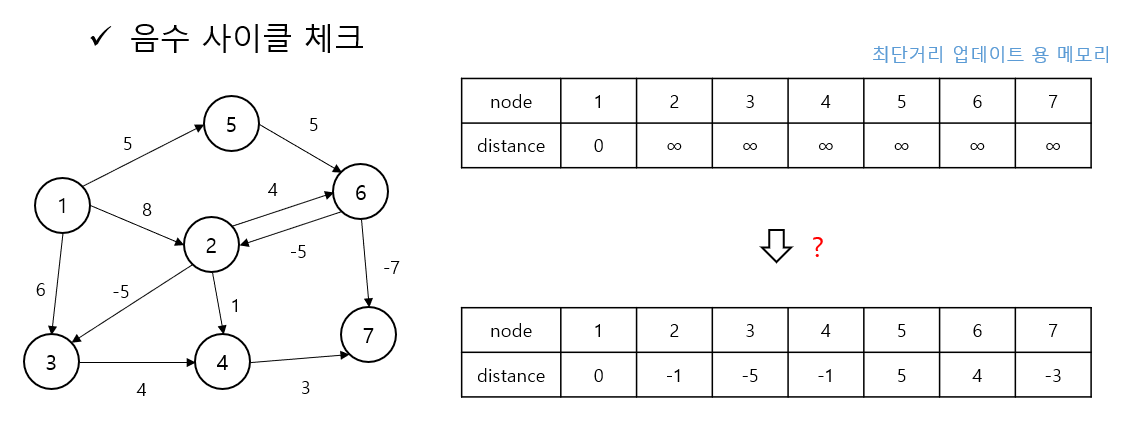
음수 싸이클

distance[2] = 8이고 distance[6] = 12로 노드 6을 왔을 때 다시 노드 2를 방문해 서로를 계속 방문하며 distance[6]의 값이 1씩 줄어들게 된다.

이럴 땐 음수 싸이클 인지 체크해줘야된다.
한 노드에서 다른 노드까지의 최단 경로는 많아봐야 V-1개의 간선을 지난다.
즉, 최단 경로가 V-1개를 돌렸을 때 최종적으로 결과가 바뀌지 않아야한다.
하지만 결과가 계속 바뀐다면 음수 싸이클이라고 알려준다.

이미지 출처 : 제로베이스

구현 방법

public class Main {
    static class Edge {
        int from, to, weight;

        public Edge(int from, int to, int weight) {
            this.from = from;
            this.to = to;
            this.weight = weight;
        }
    }
    static void bellmanFord(int v, int e, int[][] data, int start) {
        Edge[] edge = new Edge[e];
        for (int i = 0; i < e; i++) {
            edge[i] = new Edge(data[i][0], data[i][1], data[i][2]);
        }

        int[] dis = new int[v + 1];
        for (int i = 1; i <= v; i++) {
            dis[i] = Integer.MAX_VALUE;
        }
        dis[start] = 0;

        boolean isMinusCycle = false;
        for (int i = 0; i <= v; i++) {
            for (int j = 0; j < e; j++) {
                Edge cur = edge[j];

                if (dis[cur.from] == Integer.MAX_VALUE) continue;

                if (dis[cur.to] > dis[cur.from] + cur.weight) {
                    dis[cur.to] = dis[cur.from] + cur.weight;

                    if (i == v) {
                        isMinusCycle = true;
                    }
                }
            }
        }
        System.out.println("음수 사이클 발생 : "+isMinusCycle);
        for (int i = 1; i <= v; i++) {
            if (dis[i] == Integer.MAX_VALUE) System.out.print("INF ");
            else System.out.print(dis[i] + " ");
        }
        System.out.println();
    }
    public static void main(String[] args) {
    	// 음수 사이클 발생 : false
        // 0 8 3 7 5 10 3 
        int[][] data = {
                {1, 2, 8}, {1, 3, 6}, {1, 5, 5}, {2, 3, -5}, {2, 4, 1},
                {2, 6, 4}, {3, 4, 4}, {4, 7, 3}, {5, 6, 5}, {6, 2, 0},{6, 7, -7}
        };
        bellmanFord(7, 11, data, 1);
		
        // 음수 사이클 발생 : true
		// 0 -2 -6 -2 5 3 -4 
        data = new int[][]{
                {1, 2, 8}, {1, 3, 6}, {1, 5, 5}, {2, 3, -5}, {2, 4, 1},
                {2, 6, 4}, {3, 4, 4}, {4, 7, 3}, {5, 6, 5}, {6, 2, -5},{6, 7, -7}
        };
        bellmanFord(7, 11, data, 1);
    }
}