BFS (Breadth-First Search) - 너비 우선 탐색
BFS는 이름 그대로 너비를 우선으로 탐색하는 알고리즘이다. 출발 노드에서 시작해 인접한 노드들을 먼저 탐색하고 그다음 인접 노드들의 인접 노드들을 탐색해 나가는 구조다. 이렇게 하면 출발 노드로부터 거리(또는 단계)가 가까운 노드들을 먼저 방문하게 된다.
탐색 순서를 제어하기 위해 큐(Queue) 자료구조를 사용한다. 큐는 먼저 들어온 노드를 먼저 처리하는 FIFO(First-In-First-Out) 방식이기 때문에 순서대로 인접 노드를 꺼내 탐색하기에 적합하다. BFS는 일반적으로 최단 거리 탐색에 강점을 가지며 그래프가 가지는 구조 전체를 폭넓게 파악할 때 유용하다.
BFS는 완전 탐색에 가까운 구조이며 모든 노드를 방문하려면 시간 복잡도는 O(V + E)가 된다. 이 탐색은 경로의 길이를 기준으로 탐색이 진행되기 때문에 단일 시작점에서 모든 정점까지의 최단 거리를 구할 수 있다. 위키피디아에서도 이 특성을 활용해 BFS가 "길찾기, 웹 크롤링, 소셜 네트워크 분석, 라우팅 알고리즘(Dijkstra와의 조합)" 등에서 널리 쓰인다고 설명한다.
또한 BFS는 비가중치 그래프(unweighted graph)에서 두 정점 간의 최단 경로(shortest path)를 찾는 데 있어 가장 효율적인 탐색 방법이기도 하다.
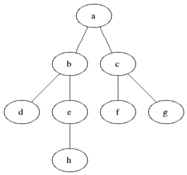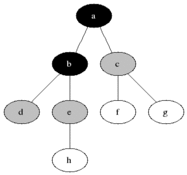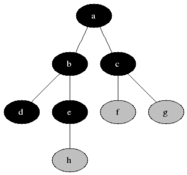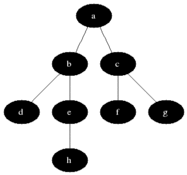
출처: https://en.wikipedia.org/wiki/Breadth-first_search
코드 예시
public void bfs(int start, List<List<Integer>> graph) {
boolean[] visited = new boolean[graph.size()];
Queue<Integer> queue = new LinkedList<>();
queue.add(start);
visited[start] = true;
while (!queue.isEmpty()) {
int curr = queue.poll();
System.out.print(curr + " ");
for (int next : graph.get(curr)) {
if (!visited[next]) {
visited[next] = true;
queue.add(next);
}
}
}
}DFS (Depth-First Search) - 깊이 우선 탐색
DFS는 어떤 노드에 도착했을 때 가능한 한 깊이까지 먼저 탐색하고 막히면 다시 돌아와 다른 경로를 탐색하는 알고리즘이다. 쉽게 말하면, “파고들 수 있을 때까지 파고든다”는 개념이다. 이를 위해 일반적으로 스택(Stack) 또는 재귀 호출을 사용한다.
스택은 후입선출(LIFO) 구조이므로 최근에 방문한 노드부터 다시 꺼내 깊이 있는 탐색을 이어갈 수 있다. 재귀 호출을 사용하면 스택을 명시적으로 구현하지 않아도 함수 호출 스택을 통해 동일한 효과를 낼 수 있다. DFS는 모든 경우의 수를 탐색해야 하는 문제, 예를 들면 조합, 순열, 백트래킹 문제 등에 매우 유용하다.
Wikipedia에 따르면 DFS는 특히 그래프의 연결성 확인, 싸이클 탐지, 위상 정렬(Topological Sorting) 등에서 자주 쓰이며 미로 탐색, 경로 존재 여부 확인, 전역 최적보다는 부분 탐색에 집중할 때 효과적이다.
또한 DFS는 백트래킹 알고리즘의 기반이 되는 탐색 방법이기도 하며 모든 경우의 수를 시도하는 문제에 필수적이다. 다만 최단 경로를 보장하지 않으며 재귀 깊이에 따른 스택 오버플로우 문제가 발생할 수 있다.
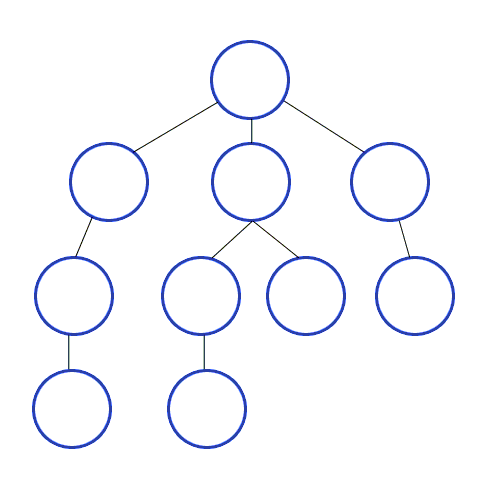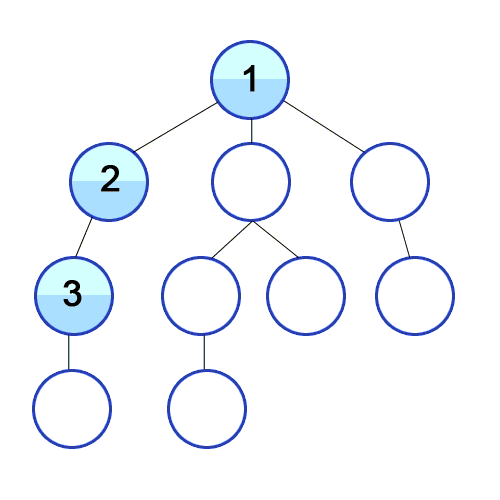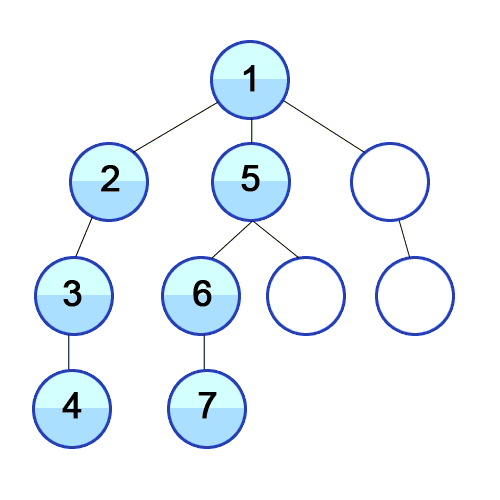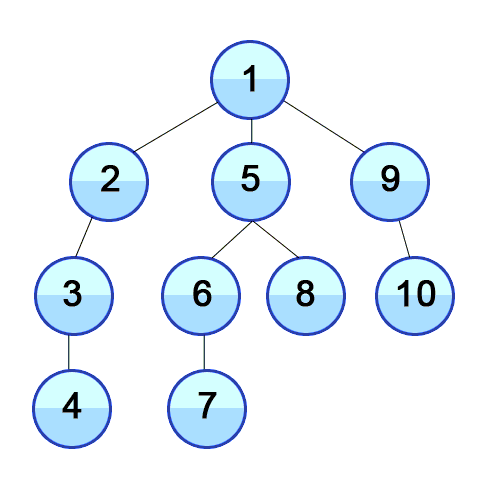
출처: https://en.wikipedia.org/wiki/Depth-first_search
코드 예시
public void dfs(int curr, List<List<Integer>> graph, boolean[] visited) {
visited[curr] = true;
System.out.print(curr + " ");
for (int next : graph.get(curr)) {
if (!visited[next]) {
dfs(next, graph, visited);
}
}
}BFS vs DFS
| 비교 항목 | BFS | DFS |
|---|---|---|
| 탐색 방식 | 가까운 노드부터 탐색 | 깊은 노드부터 탐색 |
| 자료구조 | Queue | Stack (또는 Recursion) |
| 최단 경로 탐색 | 가능 (최단 거리 보장) | 불가능 (깊은 경로 먼저 탐색) |
| 재귀 사용 | 필요 없음 | 필요함 (또는 명시적 스택 사용) |
| 사용 예시 | 미로 최단 거리, 소셜 네트워크 분석, 웹 크롤링 | 조합, 순열, 백트래킹, 싸이클 탐지, 위상 정렬 |
| 메모리 사용량 | 큐에 모든 레벨 노드 저장 -> 큼 | 재귀 깊이에 따라 다름 |
| 경로의 다양성 | 짧고 넓은 경로 위주 | 깊고 특이한 경로까지 포함 가능 |
📝 느낀 점
처음엔 BFS와 DFS가 단순히 순서 차이만 있는 탐색 방법이라고 생각했었다. 하지만 다양한 문제를 풀다 보면 두 알고리즘은 전혀 다른 특성과 장점을 가진 도구라는 걸 체감하게 된다. BFS는 "최단 거리"를 빠르게 찾는 데 탁월해서 미로 문제처럼 거리 기반의 문제에서 강점을 보인다. 탐색의 깊이보다 폭이 중요할 때, BFS는 가장 믿을 수 있는 도구다. 반대로 DFS는 "끝까지 파고드는 탐색"이 가능해서 모든 경우의 수를 시도해야 하는 백트래킹 문제에서 거의 필수로 쓰인다.
Wikipedia를 참고하며 인상 깊었던 점은 두 알고리즘이 단순한 탐색을 넘어서 각종 실전 문제에 광범위하게 사용된다는 점이었다. 예를 들어 BFS는 네트워크에서 라우팅 경로 탐색에 적용되고 DFS는 사이클 검출이나 위상 정렬에 적용된다. 알고리즘 문제 풀이를 넘어서, 실제 시스템 구조나 최적화 문제에까지 활용된다는 사실이 알고리즘 공부의 동기를 더 키워주었다.
결국 중요한 건 문제의 성격에 따라 적절한 탐색 방법을 선택하는 것이다. "단계적으로 가까운 것을 우선해야 한다면 BFS", "모든 경로를 시도하거나 깊이 있는 경로를 찾고 싶다면 DFS"라는 기준을 세우고 접근하면 문제 풀이에 훨씬 도움이 된다. 앞으로도 알고리즘 문제를 풀 때 단순히 구현만 하는 것이 아니라, 왜 이 탐색을 쓰는지, 장단점은 무엇인지를 함께 설명할 수 있을 정도로 깊이 있는 이해를 계속 쌓아가야겠다.
참고
