시간 복잡도란? (Big-O 표기법)

시간 복잡도란?

알고리즘의 성능을 나타내는 지표로, 입력 크기에 대한 연산 횟수의 상한을 의미한다.
※ 시간 복잡도는 주로 빅오 표기법을 사용해 나타낸다.

빅오(Big-O) 표기법

최악의 상황으로 연산량을 계산하는 표기법
"이 정도 시간이 걸린다"보다는 "이 정도 시간까지 걸릴 수 있다"라고 생각하는 게 좋은 거 같다.

• 배열에서 1을 찾는데 마지막이 1인 경우

이미지 출처

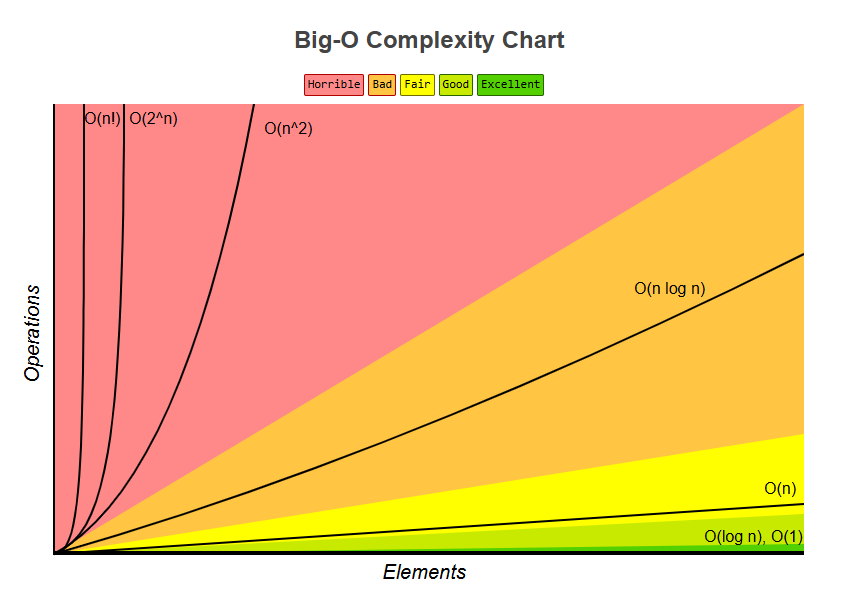
O(1) - 상수 시간

처리해야할 데이터양(입력크기)와 상관없이 항상 일정한 연산량을 갖고 있는 알고리즘

for(int i=1; i<=10; i++) {
	sum += i;
}

O(logN) - 로그 시간

입력 크기 N이 증가할 때 알고리즘의 실행 시간이 로그 함수 형태로 증가하는 것. 이진 탐색이 해당된다.

static int binarySearch(int[] array, int target) {
    int left = 0;
    int right = array.length - 1;

    while (left <= right) {
        int mid = left + (right - left) / 2;

        if (array[mid] == target) {
            return mid;
        }
        if (array[mid] < target) {
            left = mid++;
        } else {
            right = mid--;
        }
     }
    return -1; // 타겟을 찾지 못한 경우
}

O(N) - 선형 시간

처리해야할 데이터양과 비례해 연산량도 증가하는 알고리즘

for(int i=1; i<=n; i++) {
	sum += i;
}

O(NlongN) - 로그 선형 시간

입력 크기 N에 대해 로그 시간 복잡도를 가진 알고리즘을 여러 번 수행하는 경우. 대표적인 예로는 퀵 정렬(Quick Sort)과 병합 정렬(Merge Sort)

static void quickSort(int[] array, int low, int high) {
    if (low < high) {
        int pivotIndex = partition(array, low, high);
        quickSort(array, low, pivotIndex - 1);
        quickSort(array, pivotIndex + 1, high);
    }
}

static int partition(int[] array, int low, int high) {
    int pivot = array[high];
    int i = low - 1;
    for (int j = low; j < high; j++) {
        if (array[j] < pivot) {
            i++;
            int temp = array[i];
            array[i] = array[j];
            array[j] = temp;
        }
    }
    int temp = array[i + 1];
    array[i + 1] = array[high];
    array[high] = temp;
    return i + 1;
}

O(N²) - 이차 시간

이중 반복문일 경우. 버블 정렬, 선택정렬 등이 해당된다.

public static void bubbleSort(int[] array) {
    int n = array.length;
    
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - i - 1; j++) {
            if (array[j] > array[j + 1]) {
                int temp = array[j];
                array[j] = array[j + 1];
                array[j + 1] = temp;
            }
        }
    }
}

O(2^N) - 지수 시간

N에 대해 알고리즘의 실행 시간이 지수적으로 증가하는 경우. 파보나치 수열이 해당됨

static int fibonacci(int n) {
	if(n<=1) return n;
    return fibonacci(n-1) + fibonacci(n-2);
}

빅오메가(Big-Ω) 표기법

최선의 상황으로 연산량을 계산하는 표기법

• 배열에서 1을 찾는데 첫번 째가 1인 경우

빅세타(Big-θ) 표기법

최악과 최선의 평균으로 연산량을 계산하는 표기법

• 배열에서 1을 찾는데 중간인 경우