문제코드

class Heap {
    constructor(compare) {
        this.heap = [];
        this.compare = compare;
    }
    swap(a, b) {
        [this.heap[a], this.heap[b]] = [this.heap[b], this.heap[a]];
    }
    size() {
        return this.heap.length;
    }
    push(value) {
        this.heap.push(value);
        this.upHeap();
    }
    pop() {
        if (this.size() <= 0) {
            return undefined;
        }
        this.swap(0, this.size()-1);
        const value = this.heap.pop();
        this.downHeap(0);
        return value;
    }
    upHeap() {
        let current = this.size()-1;
        while (0 < current) {
            const parent = Math.floor((current - 1) / 2);
            if (this.compare(this.heap[parent], this.heap[current])) {
                return;
            }
            this.swap(parent, current);
            current = parent;
        }
    }
    downHeap(i) {
        let current = i;
        while (current < this.size()) {
            const left = current * 2;
            const right = current * 2 + 1;
            
            if (!this.heap[left]) {
                break;
            }
            if (!this.heap[right]) {
                if (this.compare(this.heap[current], this.heap[left])) {
                    break;
                }
                this.swap(current, left);
                continue;
            }
            const next = this.compare(this.heap[left], this.heap[right]) ? right : left; // 더 작은쪽
            if (this.compare(this.heap[current], this.heap[next])) {
                break;
            }
            this.swap(current, next);
            current = next;
        }
    }
}

function solution(n, paths, gates, summits) {
    const isSummits = Array.from({length:n+1}, () => false);
    const intensity = Array.from({length:n+1}, () => Infinity);
    const graph = {};
    const pq = new Heap((parent, child) => {
        return parent[1] <= child[1];
    })
    
    for(let i=1; i<=n; i++) {
        graph[i] = [];
    }
    
    paths.forEach(([ start, end, inst ]) => {
        graph[start].push([end, inst]);
        graph[end].push([start, inst]);
    });
    
    summits.forEach((summit) => {
        isSummits[summit] = true;
    });
    
    gates.forEach((gate) => {
        pq.push([gate, 0]);
        intensity[gate] = 0;
    });
    
    while(0 < pq.size()) {
        const [idx, inst] = pq.pop();
        const nexts = graph[idx];

        if (isSummits[idx] || intensity[idx] < inst) {
            continue;
        }

        nexts.forEach(([end, nextInst]) => {
            const totalInst = Math.max(inst, nextInst)
            if (intensity[end] <= totalInst) {
                return;
            }
            intensity[end] = totalInst;
            pq.push([end, totalInst]);
        });
    }
    
    return summits.sort((a,b) => a-b).reduce((acc, summit) => {
        if (intensity[summit] < acc[1]) {
            return [summit, intensity[summit]];
        }
        return acc;
    }, [-1, Infinity]);
}

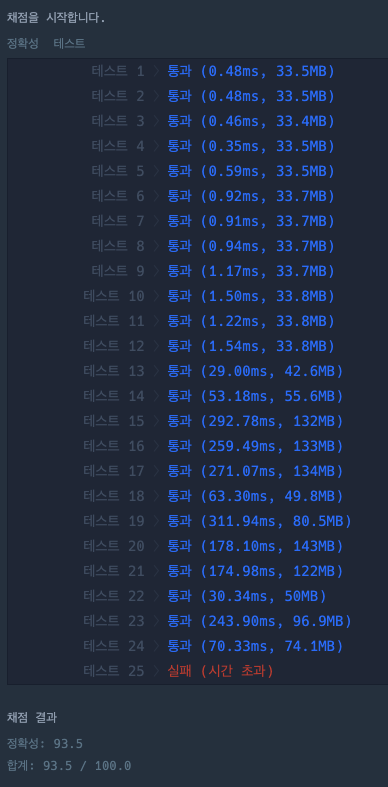
우선순위 큐를 사용한 다익스트라 알고리즘을 사용해서 해결했다. 테스트 24번까지 잘 돌아가는 걸 보고 맞았다! 싶었는데, 테스트 25에서 시간초과가 발생했고, 알고리즘 상으로는 시간복잡도가 초과하지 않아야 했다.

문제 원인과 해결

기존까지 한번 작성해둔 우선순위 큐가 큰 문제 없이 작동했기 때문에 이 부분이 문제다! 라는 생각을 늦게 했다.

확실히 C++이나 파이썬과 같이 기본으로 제공해주는 자료구조가 없다보니, 동작은 흉내내더라도 최적화된 자료구조로 사용하기에는 어려움이 있는 것 같다.

요즘 들어 이런 문제를 발견하면 사용하는 방법이 있는데, 바로 요즘 핫한 ChatGPT다.

간단하게 궁금한 점을 물어보는 것 부터, 최근에는 프론트엔드 모의 면접을 면접관 입장에서 진행해달라고 요청했더니 정말 비슷하게 진행해줬다.

그래서 이번에도 ChatGPT에게 효율적인 코드 작성을 요청했다.

class PriorityQueue {
  constructor(comparatorFunction) {
    this.heap = [];
    this.compare = comparatorFunction || ((a, b) => a - b);
  }

  enqueue(item) {
    this.heap.push(item);
    this.heapifyUp();
  }

  dequeue() {
    const max = this.heap[0];
    const end = this.heap.pop();
    if (this.heap.length > 0) {
      this.heap[0] = end;
      this.heapifyDown();
    }
    return max;
  }

  heapifyUp() {
    let index = this.heap.length - 1;
    while (index > 0) {
      const element = this.heap[index];
      const parentIndex = Math.floor((index - 1) / 2);
      const parent = this.heap[parentIndex];
      if (this.compare(parent, element) >= 0) {
        break;
      }
      this.heap[index] = parent;
      this.heap[parentIndex] = element;
      index = parentIndex;
    }
  }

  heapifyDown() {
    let index = 0;
    const length = this.heap.length;
    const element = this.heap[0];
    while (true) {
      const leftChildIndex = 2 * index + 1;
      const rightChildIndex = 2 * index + 2;
      let leftChild, rightChild;
      let swap = null;

      if (leftChildIndex < length) {
        leftChild = this.heap[leftChildIndex];
        if (this.compare(leftChild, element) > 0) {
          swap = leftChildIndex;
        }
      }
      if (rightChildIndex < length) {
        rightChild = this.heap[rightChildIndex];
        if (
          (swap === null && this.compare(rightChild, element) > 0) ||
          (swap !== null && this.compare(rightChild, leftChild) > 0)
        ) {
          swap = rightChildIndex;
        }
      }
      if (swap === null) {
        break;
      }
      this.heap[index] = this.heap[swap];
      this.heap[swap] = element;
      index = swap;
    }
  }
}

정답 코드

ChatGPT가 작성해준 우선순위 큐를 사용하면 아래와 같은 코드를 작성할 수 있다.

class PriorityQueue {
    constructor(comparatorFunction) {
        this.heap = [];
        this.compare = comparatorFunction || ((a, b) => a - b);
    }
    
    size() {
        return this.heap.length;
    }

    enqueue(item) {
        this.heap.push(item);
        this.heapifyUp();
    }

    dequeue() {
        const max = this.heap[0];
        const end = this.heap.pop();
        if (this.heap.length > 0) {
            this.heap[0] = end;
            this.heapifyDown();
        }
        return max;
    }

    heapifyUp() {
        let index = this.heap.length - 1;
        while (index > 0) {
            const element = this.heap[index];
            const parentIndex = Math.floor((index - 1) / 2);
            const parent = this.heap[parentIndex];
            if (this.compare(parent, element) >= 0) {
                break;
            }
            this.heap[index] = parent;
            this.heap[parentIndex] = element;
            index = parentIndex;
        }
    }

    heapifyDown() {
        let index = 0;
        const length = this.heap.length;
        const element = this.heap[0];
        while (true) {
            const leftChildIndex = 2 * index + 1;
            const rightChildIndex = 2 * index + 2;
            let leftChild, rightChild;
            let swap = null;

            if (leftChildIndex < length) {
                leftChild = this.heap[leftChildIndex];
                if (this.compare(leftChild, element) > 0) {
                    swap = leftChildIndex;
                }
            }
            if (rightChildIndex < length) {
                rightChild = this.heap[rightChildIndex];
            if ((swap === null && this.compare(rightChild, element) > 0) ||
            (swap !== null && this.compare(rightChild, leftChild) > 0)) {
                swap = rightChildIndex;
            }
        }
        if (swap === null) {
            break;
        }
        this.heap[index] = this.heap[swap];
        this.heap[swap] = element;
        index = swap;
        }
    }
}

function solution(n, paths, gates, summits) {
    const isGates = Array(n+1).fill(false);
    const isSummits = Array(n+1).fill(false);
    const intensity = Array(n+1).fill(Infinity);
    const graph = Array.from({length: n+1}, () => []);
    const pq = new PriorityQueue((a, b) => a[1] <= b[1]);
    
    paths.forEach(([ start, end, inst ]) => {
        graph[start].push([end, inst]);
        graph[end].push([start, inst]);
    });

    gates.forEach((gate) => {
        isGates[gate] = true;
        pq.enqueue([gate, 0]);
        intensity[gate] = 0;
    });
    summits.forEach((summit) => {
        isSummits[summit] = true;
    });
    
    graph.map((path, start) => {
        if (isSummits[start]) {
            return [];
        }
        return path.filter(([end, inst]) => {
            return !isGates[end];
        });
    });
    
    while(0 < pq.size()) {
        const [idx, inst] = pq.dequeue();

        if (isSummits[idx] || intensity[idx] < inst) {
            continue;
        }

        graph[idx].forEach(([end, nextInst]) => {
            const totalInst = Math.max(inst, nextInst)
            if (totalInst < intensity[end]) {
                intensity[end] = totalInst;
                pq.enqueue([end, totalInst]);
            }
        });
    }
    
    return summits.sort((a,b) => a-b).reduce((acc, summit) => {
        if (intensity[summit] < acc[1]) {
            return [summit, intensity[summit]];
        }
        return acc;
    }, [-1, Infinity]);
}

결과는 아래와 같다.

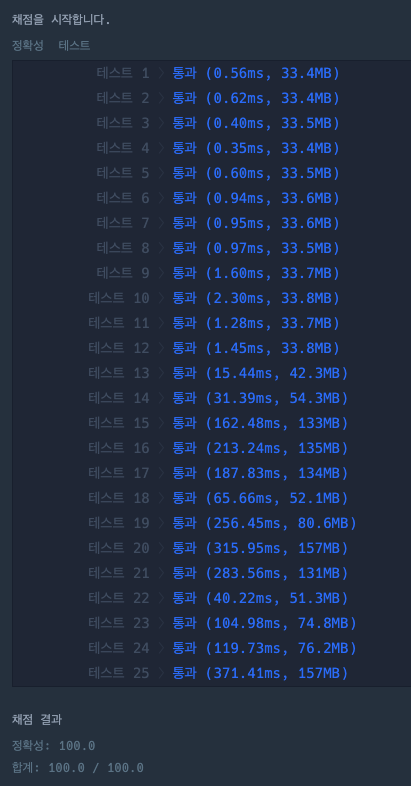
자료구조 교체 하나만으로 완전 효율적인 코드가 되어버렸다.

이걸 계기로 기존에 작성하던 알고리즘 문제풀이를 위한 자료구조를 한번 싹 정리해야겠다는 생각이 들었다.