[Algorithm] 정렬

정렬 알고리즘(Sorting Algorithm)

• 원소들을 번호 순이나 사전 순서와 같이 일정한 순서대로 열거하는 알고리즘
• 효율적인 정렬은 탐색이나 병합 알고리즘처럼(정렬된 리스트에서 바르게 동작하는) 다른 알고리즘을 최적화하는 데 중요함 . 또 정렬 알고리즘은 데이터의 정규화나 의미있는 결과물을 생성하는 데 흔히 유용하게 쓰임

---

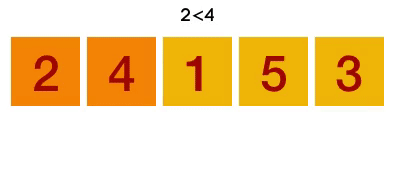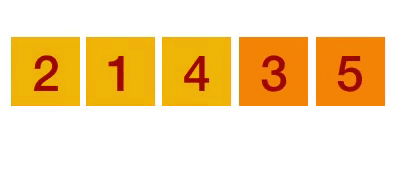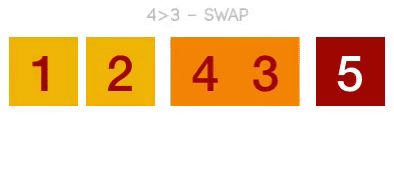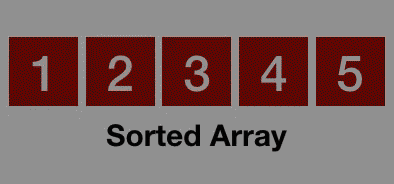
1. 버블 정렬(Bubble sort)

• 두 인접한 원소를 검사하여 정렬하는 방법
• 시간복잡도 : O(n^2)
• 시간 복잡도가 느리지만, 코드가 단순하기 때문에 자주 사용됨
  

def bubble_sort(arr):
  for i in range(len(arr)):
      for j in range(i, len(arr)):
          if arr[j-1] < arr[j]:
              arr[j-1], arr[j] = arr[j], arr[j-1]
  return arr

---

2. 선택 정렬(Selection Sort)

• bouble sort 차이점 : min_idx 추가, min_idx를 찾고 나서 변경
• 과정 :
  • 주어진 데이터 중 , 최소값(min_idx)를 찾는다.
  • 최소값을 리스트 맨 앞의 위치한 값과 바꾼다.
  • 맨 앞의 위치를 뺀 나머지 데이터를 동일한 방법으로 반복한다.
• 시간복잡도 : O(n^2)
  

def selection_sort(arr):
    for i in range(len(arr) - 1):
        min_idx = i
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[min_idx]:
                min_idx = j
        arr[i], arr[min_idx] = arr[min_idx], arr[i]

---

3. 삽입 정렬(Insertion Sort)

• 이미 정렬된 배열을 유지하며, 새로운 숫자가 삽입되면 정렬된 배열 안에서 자기의 자리를 찾아가며 정렬
• 시간복잡도 : O(n^2)
  

def insertion_sort(arr):
    for end in range(1, len(arr)):
        i = end
        while i > 0 and arr[i - 1] > arr[i]:
            arr[i - 1], arr[i] = arr[i], arr[i - 1]
            i -= 1

---

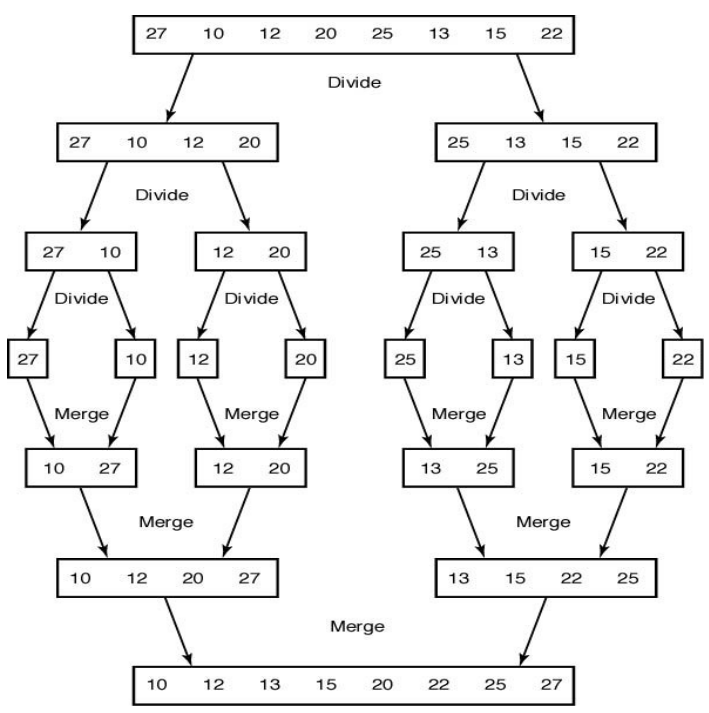
4. 병합 정렬(Merge Sort)

• 원소가 하나 밖에 남지 않을 때까지 계속 둘로 쪼갠 후에 다시 크기 순으로 재배열 하면서 원래 크기의 배열로 합침
• 분할 정복(Devide and Conquer) 기법 + 재귀용법
• 과정
  • 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눔
  • 이 과정을 리스트가 하나가 남을 때까지 반복 (DC/재귀)
  • 정렬
  • 두 부분 리스트들을 다시 하나의 리스트로 합병
• 알고리즘의 구성을 '분리 단계'와 '합병 단계'로 나눌 수 있음