코드
# 2023-02-23 15:39:44
# https://www.acmicpc.net/problem/1074
import sys
input = sys.stdin.readline
n, r, c = map(int, input().split())
ans = 0
while n > 0 :
# 2**(n-1)을 기준으로 Z 모양의 위치를 정함
n -= 1
if r < 2**n and c < 2**n : # Z의 0번째 위치
r, c = r, c
ans += (2**n)**2 * 0
elif r < 2**n and c >= 2**n : # Z의 1번째 위치
r, c = r, abs(2**n - c)
ans += (2**n)**2 * 1
elif r >= 2**n and c < 2**n : # Z의 2번째 위치
r, c = abs(2**n - r), c
ans += (2**n)**2 * 2
elif r >= 2**n and c >= 2**n : # Z의 3번째 위치
r, c = abs(2**n - r), abs(2**n - c)
ans += (2**n)**2 * 3
print(ans)풀이노트
문제 이해
2^N X 2^N 숫자를 가지고, 2^(N-1) X 2^(N-1) 등분하여 Z자 모양으로 탐색한다.
N = 1 일 때는 다음과 같다.
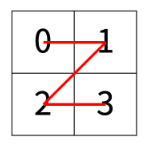
N = 2 일 때는 다음과 같다.
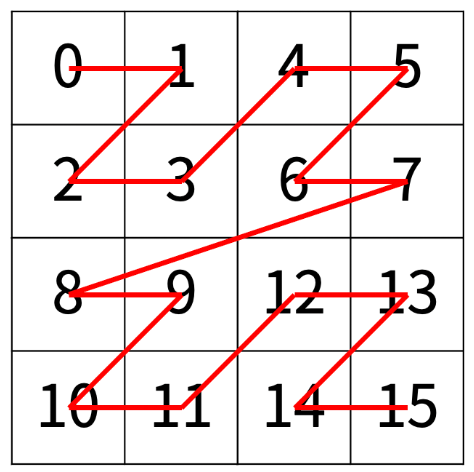
N = 3 일 때는 다음과 같다.
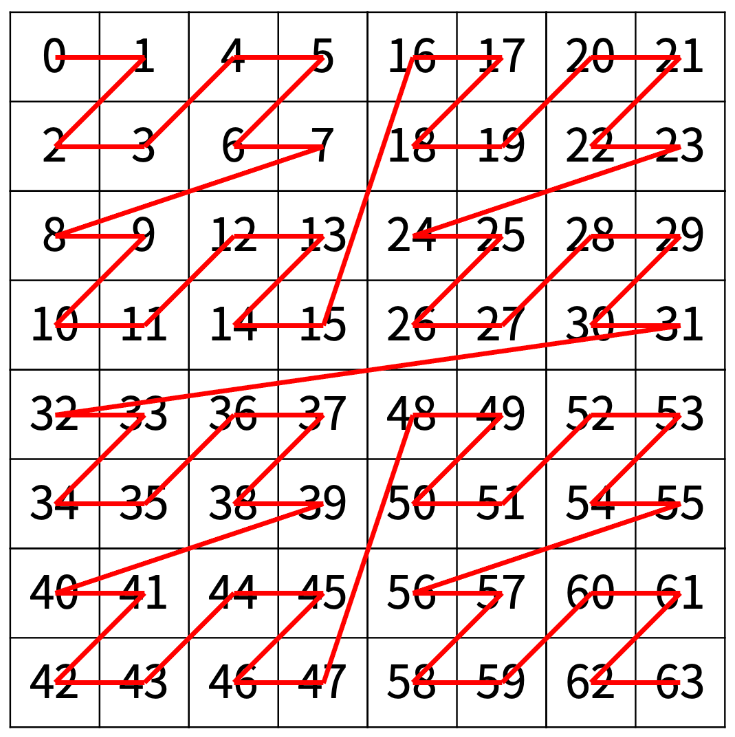
예제 입력1 - 2X2 일 때
예제 입력1을 참고하여 (2, 3, 1) 일 때를 생각해보자.
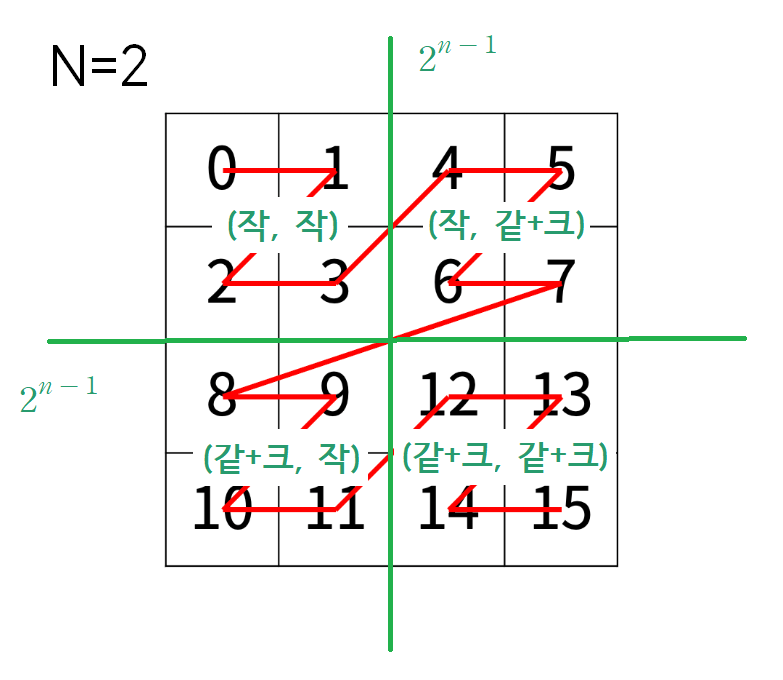
N = 2 일 때, 4 X 4 모양을 가진다.
이 때 2^(N-1) 선을 기준으로, 큰 Z를 생성하고, 큰 Z의 원소 내에는 작은 Z를 가진다. 큰 Z로부터 작은 Z로 접근해야 한다.
Z의 패턴을 살펴보자.
2^(N-1) 선을 기준으로, r과 c의 값에 따라 Z 영역을 가진다.
그림과 같이 선을 기준으로 (r, c)가 2^(n-1)보다 (작, 작)인 경우에는 Z의 0 부분을, (작, 같+크)인 경우에는 Z의 1 부분을, (같+크, 작)인 경우에는 Z의 2 부분을, (같+크, 같+크)인 경우에는 Z의 3 부분을 가진다.
이를 코드로 작성하면 다음과 같다.
if r < 2**n and c < 2**n : # Z의 0번째 위치
...
elif r < 2**n and c >= 2**n : # Z의 1번째 위치
...
elif r >= 2**n and c < 2**n : # Z의 2번째 위치
...
elif r >= 2**n and c >= 2**n : # Z의 3번째 위치
...큰 Z의 0/1/2/3 위치 중 어디에 위치하였는지 확인하고, 다시 작은 Z로 접근하여 0/1/2/3 위치를 파악하면 된다.
큰 Z의 위치에 따라 (0, 0) 위치에 놓인 값들이 다르다.
이것의 패턴을 분석해 보자.
N = 1일 때, 0 → 1 → 2 → 3 으로 2^0 만큼씩 증가한다.
N = 2일 때, 0 → 1 → 2 → 3 으로 (2^1)^2 만큼씩 증가한다.
N = 3일 때, 0 → 16 → 32 → 48 으로 (2^2)^2 만큼씩 증가한다.
큰 Z에서 한 변의 길이는 2^N 이고, 작은 Z에서 한 변의 길이는 2^(N-1)이다. 따라서 작은 Z는 (2^(N-1))^2개의 원소를 가지므로, 작은 Z 간의 공차는 (2^(N-1))^2가 된다.
따라서 이를 코드로 나타내보면 다음과 같다.
if r < 2**n and c < 2**n : # Z의 0번째 위치
ans += (2**n)**2 * 0
elif r < 2**n and c >= 2**n : # Z의 1번째 위치
ans += (2**n)**2 * 1
elif r >= 2**n and c < 2**n : # Z의 2번째 위치
ans += (2**n)**2 * 2
elif r >= 2**n and c >= 2**n : # Z의 3번째 위치
ans += (2**n)**2 * 3큰 Z에서 탐색이 끝나면 작은 Z로 이동해 그 위치를 파악한다.
이 때 r, c의 값을 수정해주어야 한다.
위의 그림에서 r 또는 c의 값이 기준인 2^(N-1) 보다 큰 경우, 다음 Z 탐색을 위해서 2^(N-1) 보다 작게 만들어줘야 한다.
이를 코드로 반영해보자.
if r < 2**n and c < 2**n : # Z의 0번째 위치
r, c = r, c
ans += (2**n)**2 * 0
elif r < 2**n and c >= 2**n : # Z의 1번째 위치
r, c = r, abs(2**n - c)
ans += (2**n)**2 * 1
elif r >= 2**n and c < 2**n : # Z의 2번째 위치
r, c = abs(2**n - r), c
ans += (2**n)**2 * 2
elif r >= 2**n and c >= 2**n : # Z의 3번째 위치
r, c = abs(2**n - r), abs(2**n - c)
ans += (2**n)**2 * 3이 과정을1X1 배열이 나올 때까지 반복하면 된다.
while n > 0 :
# 2**(n-1)을 기준으로 Z 모양의 위치를 정함
n -= 1
if r < 2**n and c < 2**n : # Z의 0번째 위치
r, c = r, c
ans += (2**n)**2 * 0
elif r < 2**n and c >= 2**n : # Z의 1번째 위치
r, c = r, abs(2**n - c)
ans += (2**n)**2 * 1
elif r >= 2**n and c < 2**n : # Z의 2번째 위치
r, c = abs(2**n - r), c
ans += (2**n)**2 * 2
elif r >= 2**n and c >= 2**n : # Z의 3번째 위치
r, c = abs(2**n - r), abs(2**n - c)
ans += (2**n)**2 * 3예제 입력2 - 3X3 일 때
예제 입력2을 참고하여 (3, 7, 7) 일 때를 생각해보자.
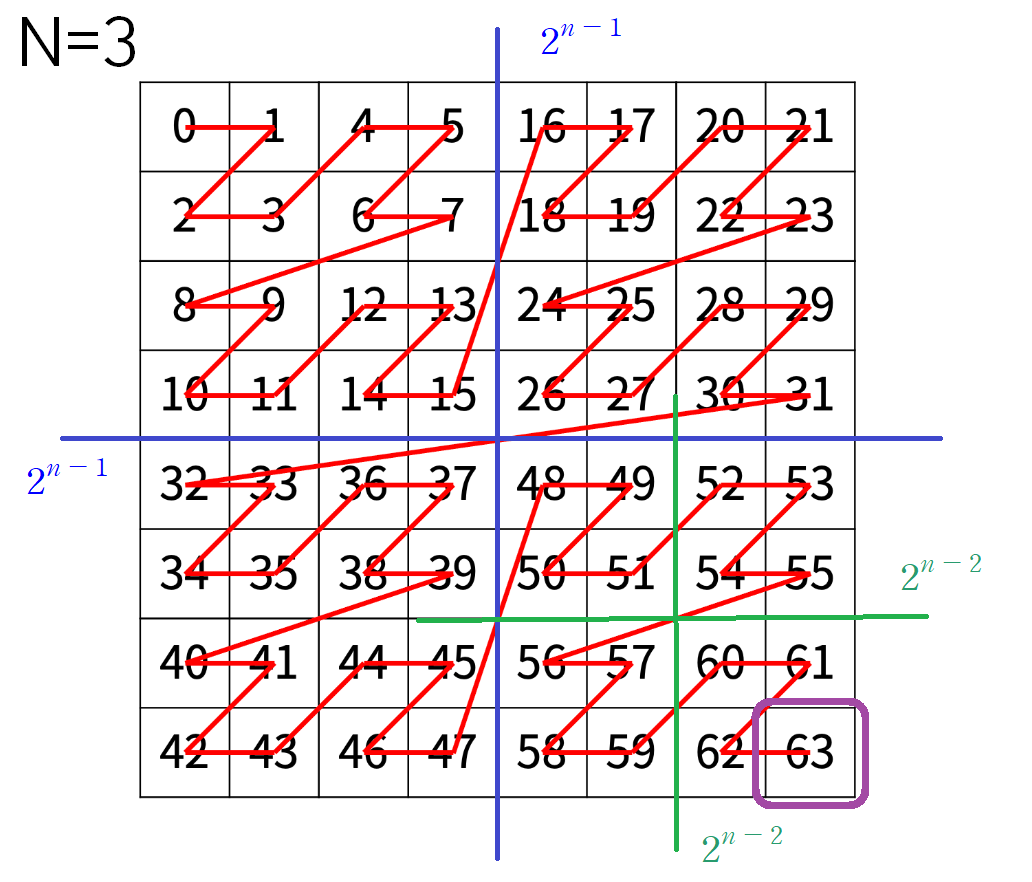
8X8 배열에서 Z 탐색이 시작된다.
첫번째 Z에서의 기준은 4가 된다.
- (r, c) 값이 모두 4보다 작을 때 (작, 작) → 0부터 시작하는 4X4 배열을 탐색
- r은 4보다 작고 c은 4보다 크거나 같을 때 (작, 같+크) → 16부터 시작하는 4X4 배열을 탐색
- r은 4보다 크거나 같고 c은 4보다 작을 때 (같+크, 작) → 32부터 시작하는 4X4 배열을 탐색
- (r, c) 값이 모두 4보다 크거나 같을 때 (같+크, 같+크) → 48부터 시작하는 4X4 배열을 탐색
여기서는 (7, 7)이 모두 4보다 크므로, (2^2)^2 * 3 (=48)부터 시작하는 4X4 배열을 대상을 한다. 이 때 (r, c) 값은 (3, 3)으로 변경하여 4X4 배열을 탐색한다.
두번째 Z에서의 기준은 2가 된다.
(3, 3)은 모두 2보다 크므로, 48 + (2^1)^2 * 3 (=48+12=60)부터 시작하는 2X2 배열을 대상으로 하고, (r, c)는 (1, 1)로 변경된다.
세번째 Z에서의 기준은 1이 된다.
(1, 1)은 모두 1보다 크거나 같으므로, 60+3을 가진다.
N = 0 이므로 while 문을 종료한다.
