[백준] 하노이 탑 이동순서_11729번

하노이 탑 이동순서_11729번

코드

def move(start, end):
    print(start, end)  # 이동좌표 출력

def hanoi(n, first, second, third):
    if(n == 1):
        move(first, third)
    else:
        hanoi(n-1, first, third, second)  # 1 ~ n-1 원반들을 두번째 장대로 이동 
        move(first, third)  # n 원반 이동
        hanoi(n-1, second, first, third)  # 1 ~ n-1 원반들을 세번째 장대로 이동

n = int(input())
count = 2**n - 1  # 원반 이동 횟수
print(count)
hanoi(n, 1, 2, 3)

풀이노트

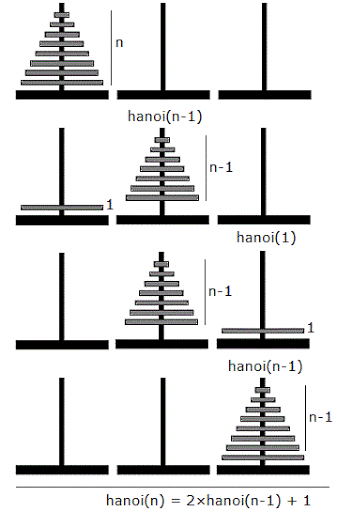
하노이 탑 알고리즘은 대표적인 재귀 호출 알고리즘 유형 중 하나임

• 재귀 알고리즘 : hanoi(n) = 2*hanoi(n-1)+1 과 같은 형식
• 이동 횟수 : 2^n − 1 회

재귀인 이유 : 젤 밑에 있는 원반을 이동하기 위해서는 두 번째 장대에 1/2/../n-1 로 쌓여있어야 함. n 원반이 세 번째 장대에 도착하면 이후는 hanoi(n-1) 과정과 동일해짐

총 원반보다 한 개 적은 탑을 옮기는데 주력할 것. 다섯 깨짜리 탑이라면 네 개의 원반을 다른 곳으로 옮기는데 주력해야 함.

-- stack으로 접근하는 것이 아닌 재귀로 접근하는 것임.
-- 감이 잡히지 않아 구글링으로 해결함 😥

소요시간 : 100분