
▶ 기본 논리 게이트
논리 게이트(Logic Gate)
- 디지털 신호를 나타내기 위해 사용되는 논리회로를 게이트(Gate)라고 한다.
- 게이트는 논리회로를 구성하는 기본 소자로서 이진 입력 정보를 이용해서 0 또는 1의 논리적인 값을 생성한다.
- AND, OR, NOT, NAND, NOR, XOR 게이트 등
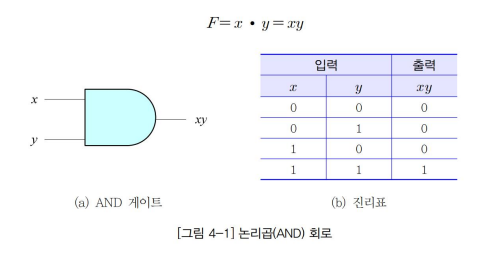
▷ 논리곱(AND) 게이트
- 두 개의 입력신호 x와 y에 대하여 xy 출력
- x ∧ y로 나타내기도 한다.
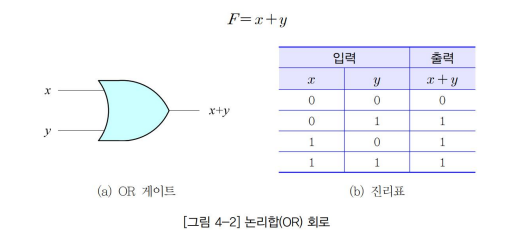
▷ 논리합(OR) 게이트
- 두 개의 입력신호 x와 y에 대하여 x + y 출력
- x ∨ y 로 나타내기도 한다.
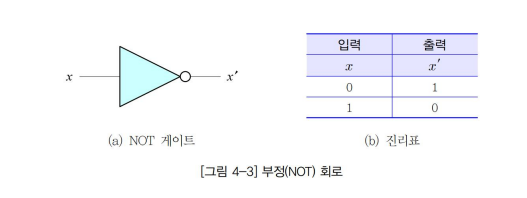
▷ 부정(NOT) 게이트
- 하나의 입력신호 x에 대하여 x´ 출력
- 인버터(Inverter)라고도 한다.
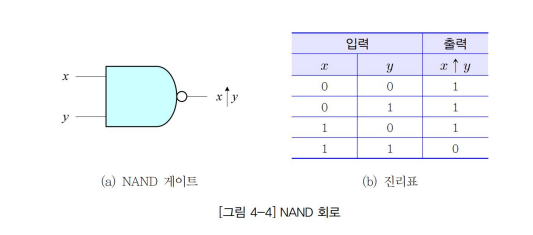
▷ NAND 게이트
- and 게이트에 not을 취하여 출력
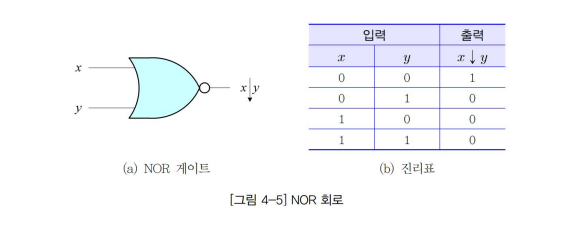
▷ NOR 게이트
- or 게이트에 not을 취하여 출력
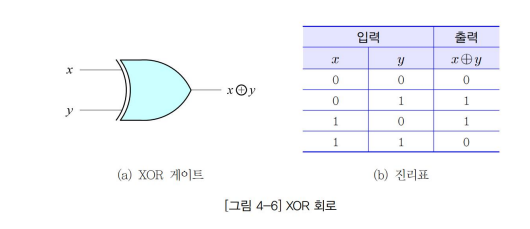
▷ 배타적 논리합(XOR) 게이트
- 입력받은 두 수가 다를 때 1을 출력, 같으면 0을 출력
▶ 부울 대수
개념
- 참과 거짓(0과 1)으로만 연산을 하는 대수학이다.
- (부울 대수(Boolean algebra) == 논리 대수(logic algebra) == 스위칭 대수(switching algebra))
- 부울 대수를 사용하면 논리식을 간략화할 수 있어 논리회로를 간소화할 수 있게 한다.
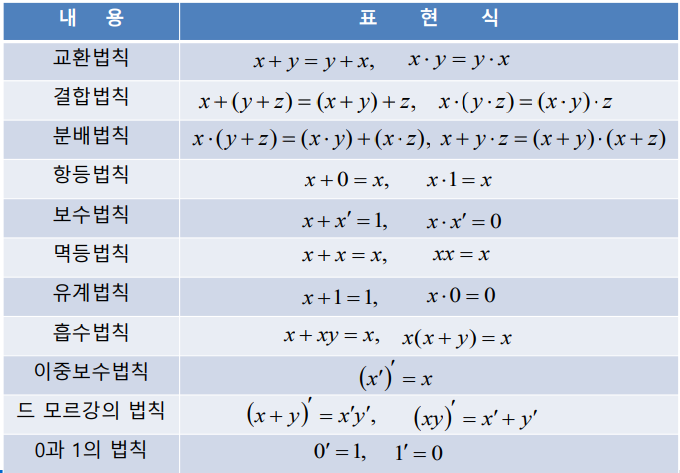
▷ 부울 대수의 정리
분배법칙 증명 ( 고맙다옹😽❤️🔥 )

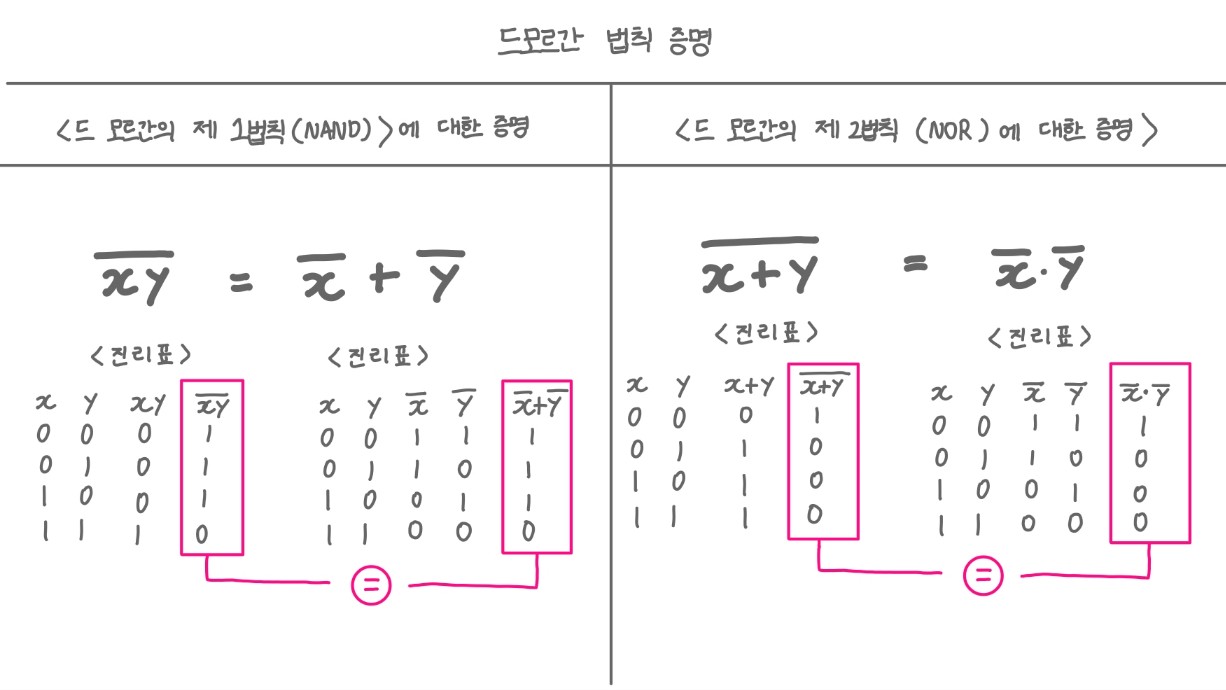
드 모르강의 법칙1 증명

드 모르강의 법칙2 증명

▶ 논리 회로의 간략화
복잡한 논리식을 최대한 간략하게 표현하기 위해 최대항, 최소항 방식을 사용한다.
▷ 정규 형태에 의한 방법
① SOP(sum of Products)
- SOP(sum of Products) : 최소항에 의한 곱들의 합을 나타내는 논리식을 말한다.
- SOP에 의거해 표준화 한 식의 값은 1이 나온다
- 표준 정규화 과정 : 모든 항에 내가 입력받은 변수가 모두 들어가도록 바꿔주는 것
- A+C의 경우 정규화가 되지 않았음, A엔 B,C가 없고 C엔 A,B가 없기 때문
SOP 정규화 과정 예제

② POS(Products of sum)
- POS(Products of sum) : 최대항에 의한 합들의 곱을 나타내는 논리식을 말한다.
- POS에 의거해 표준화 한 식의 값은 0이 나온다
- SOP와 다르게 더하기가 아닌 곱하기로 연결한다!
- SOP와 똑같이 모든 항에 내가 입력받은 변수가 모두 들어가 있어야 한다.
POS 정규화 과정 예제
- 😹도아조
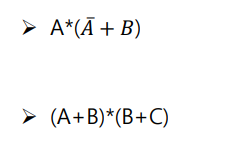
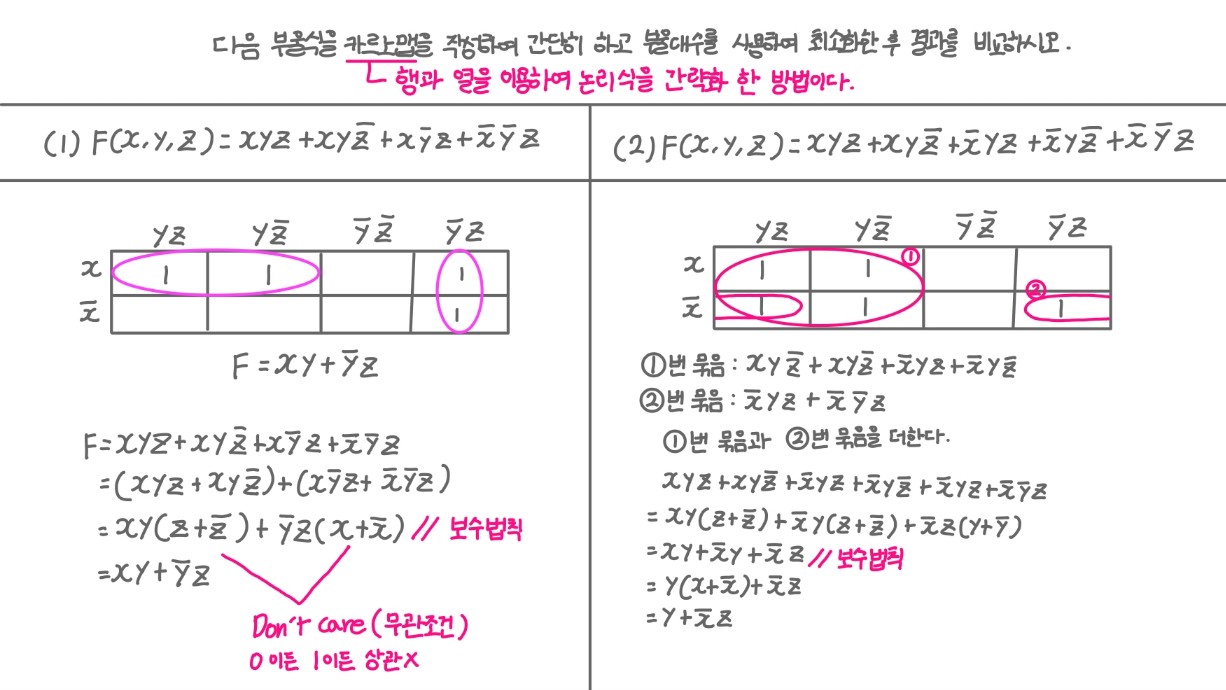
▷ 카르노맵
행과 열을 이용하여 논리식을 간략화 한 방법이다.
-
구현 방법
-
2변수의 카르노맵
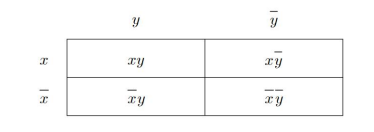
-
3변수의 카르노맵

-
카르노맵 예제⭐
-
카르노맵 그리는 방법
- 인접해 있는 항끼리 짝을 짓는다. (단, 짝수개로 묶어야 함)
- 중복해서 짝을 지을 수 있다.
- x와 x'가 함께 있다면 Don't care로 작성하지 않아도 된다.

-
(2)번 문제처럼 중복해서 그룹화 할 수 있다. (단, 무조건 짝수여야 함)
Don't care (무관) 조건
- 0이든 1이든 상관이 없다는 뜻이다.
- 즉 어떤 값이 들어오든 무관하다는 의미에서 무관 조건이라고도 한다.
- 보통 d라는 이름의 조건으로 사용된다.

🔖정리



📎참조
- 『 성결대학교 김자원 교수님 』 - 컴퓨터 구조 (2023)
- 『 컴퓨터구조(제5판) 』 - 복두 출판사
- https://circuit-designer.tistory.com/24
- https://m.blog.naver.com/war2i7i7/220820158833
