▶ ALU

• CPU에서 산술 연산과 논리 연산을 수행한다.

▷ 구성요소

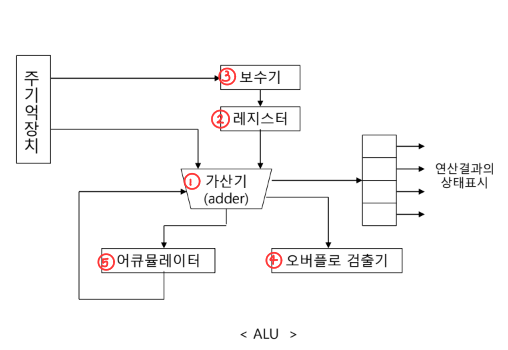
① 가산기(adder) : 덧셈 수행
② 레지스터 : 연산에 필요해서 가져온 연산 결과 임시 저장, 메모리보다 빠른 CPU내의 임시저장장치
③ 보수기 : 보수를 만들어 줌
④ 오버플로 검출기: overflow 확인
⑤ AC(누산기) : 연산 결과를 일시적으로 보존 or 중간값

▷ 기능

연산에 사용되는 데이터의 수에 따라 단항 연산(unary)과 2진(binary)으로 나뉜다.

• 단항 연산
  • 한 개의 자료에 대해서 연산을 수행
  • ex) shift, move 등

• 2진 연산(=이항 연산)
  • 두 개의 자료에 대해서 연산을 수행
  • ex) AND, OR, 사칙연산 등

주기억 장치에 저장되었던 데이터를 레지스터에 입력 -> CPU는 레지스터 통해 데이터 저장

• 레지스터의 개수 ↑ ∝ 연산속도 ↑
• 비트수 ↑ ∝ 정확도 ↑

연산의 종류

• 시프트 레지스터(shift register)

  • 비트들을 좌측 혹은 우측으로 이동시키는 기능을 하는 레지스터
  • 데이터를 레지스터에서 다른 레지스터로 복사하거나 연산을 수행하기 위해 사용

• 상태 레지스터 (Status Register 또는 Flag Register)

  • 연산 결과의 상태를 나타내는 플래그(flag)를 저장하는 레지스터
  • 조건 코드, 오버플로우, 제로 플래그 등의 프로세스의 상태 정보를 저장하는 데 사용

---

▶ 수의 표현 방법

▷ 문자 데이터의 표현

• 이전 포스팅 숫자 및 문자 코드에서 EBCDIC는 내부 통신 코드, ASCII는 외부 통신 코드라고 하였다.
• EBCDIC나 내부 ASCII로 입력을 하는 컴퓨터에서는 입력된 코드 그대로 기억하지만,
• ASCII로 입력을 하는 컴퓨터에서는 외부 통신 코드이므로 BCDIC 또는 내부 ASCII로 변환한 후 기억해야한다.

---

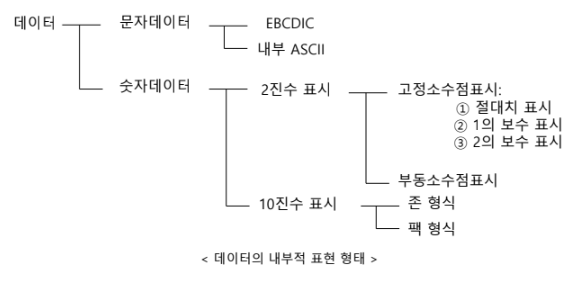
▶ 숫자 데이터의 표현

숫자 데이터를 컴퓨터 내부에서 표현하는 방식은 2진화 10진수의 경우와 2진수의 경우가 다르다.

▷ 2진화 10진 코드

2진화 10진 코드는 표현 방식에 따라 존 형식과 팩 형식으로 나뉜다.

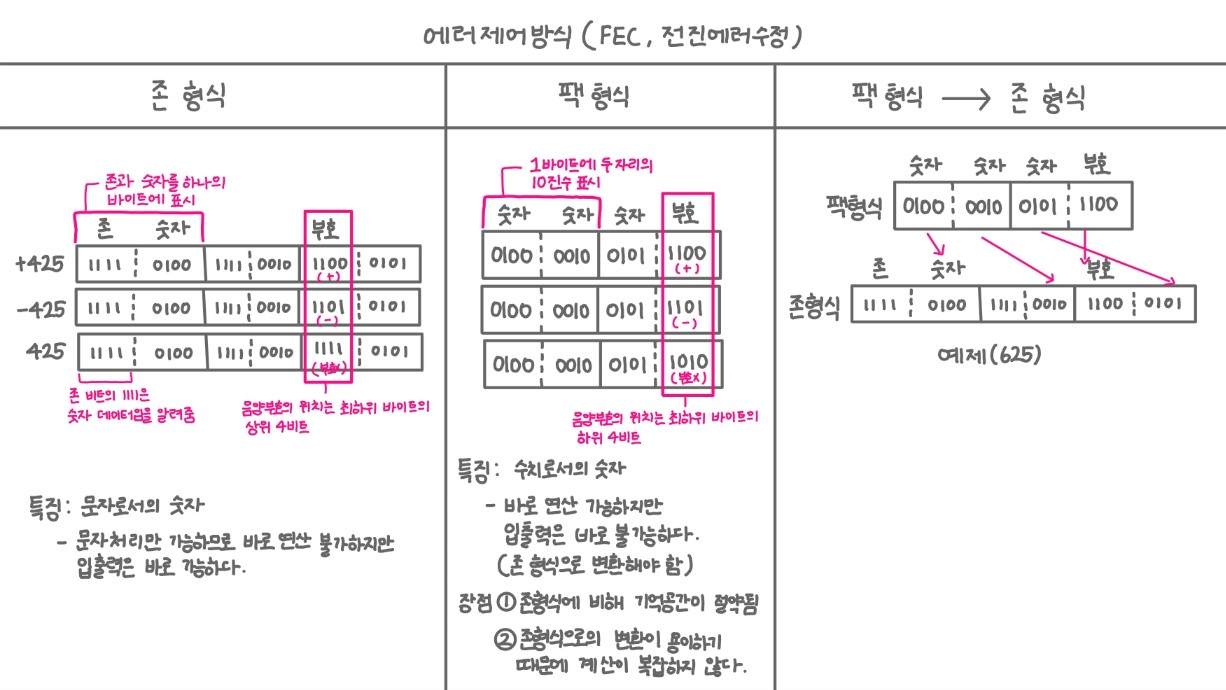
① 존 형식

개념

존 형식은 문자로서의 숫자를 말한다!
즉, 문자 처리만 가능하므로 바로 연산이 불가능하지만 입출력은 바로 가능하다.

방식

• 존 비트의 1111은 숫자 데이터임을 알려준다.

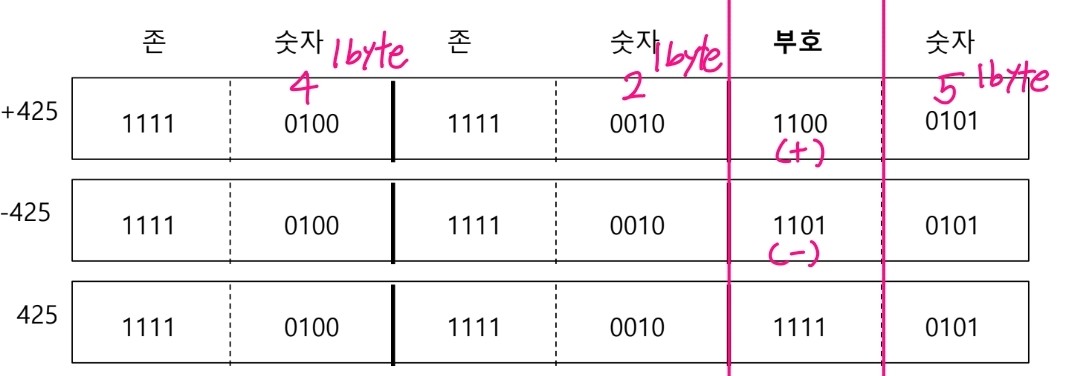
• 존과 숫자를 하나의 바이트에 표시한다.

  • 즉, 10진수 하나를 1byte에 표시하는 것이다
  • 총 3바이트로 구성된다.

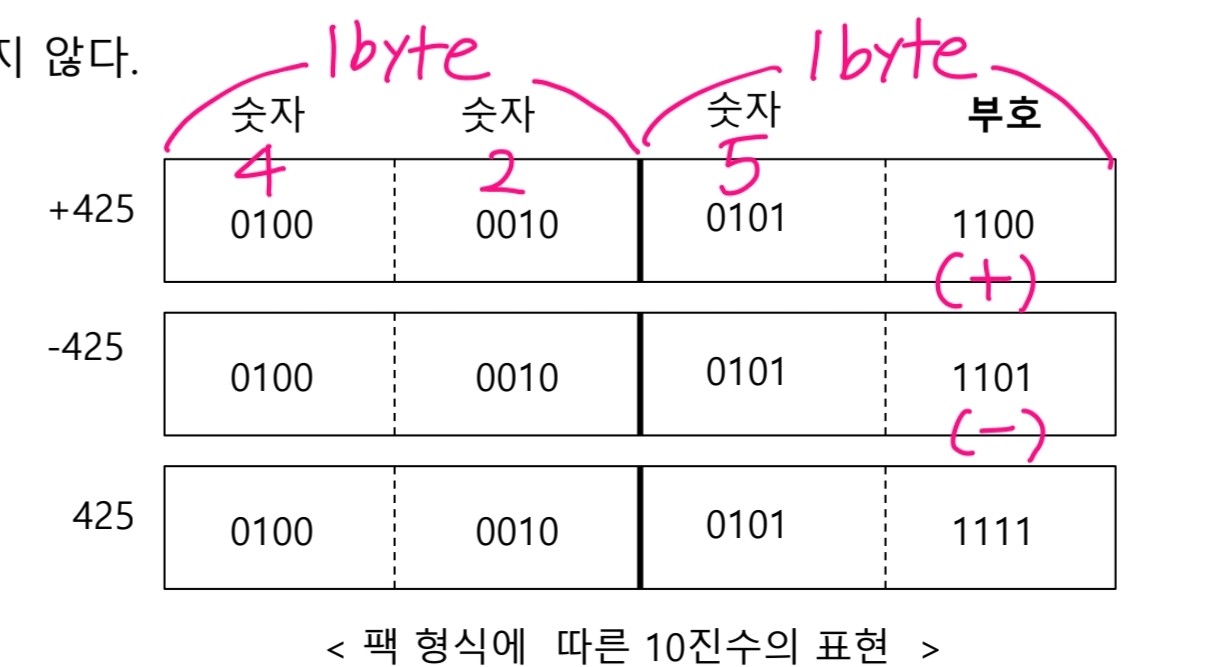
• 음양 부호의 위치는 최하위 바이트의 상위 4비트이다.

  • (+) : 1100, (-) : 1101, (부호없음) : 1111

② 팩 형식

개념

• 팩 형식은 수치로서의 숫자를 말한다!
• 바로 연산이 가능하지만, 입출력을 하기 위해 존 형식으로 변환해야 한다.

방식

• 한 바이트에 두 자리의 10진수를 표시하는 방식이다.
• 음양 부호의 위치는 최하위 바이트의 하위 4비트이다.

장점

• 존 형식에 비해 기억 공간이 절약된다.
  • 1 byte에 두 자리 10진수를 나타낼 수 있기 때문
• 존 형식(문자 코드)으로의 변환이 용이하기 때문에 계산이 복잡하지 않다.

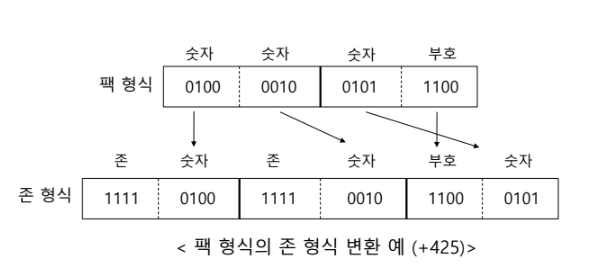
③ 팩 형식 -> 존 형식 변환

▷ 2진수 (음수의 표현 방법)

① 절대치 표현

개념

• 절대값을 기준으로 +, - 부호 비트를 바꿔주면서 표현하는 방식을 말한다.
• n-1개의 비트는 값이 변경되지 않으므로 절대치로 표현한다.

구현 방식

• 맨 좌측 비트는 부호비트(n개의 비트), 나머지 비트들은 수의 크기를 나타낸다.
• 수의 크기 비트들은 2진수를 10진수로 변환시켜 표현한다.

예시 1) +8과 -8의 절대치

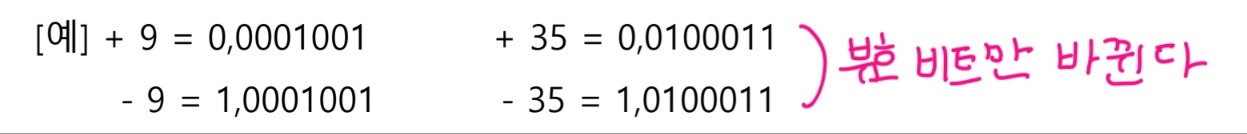
예시 2) 절대치로 표현된 2진수를 10진수로 변환

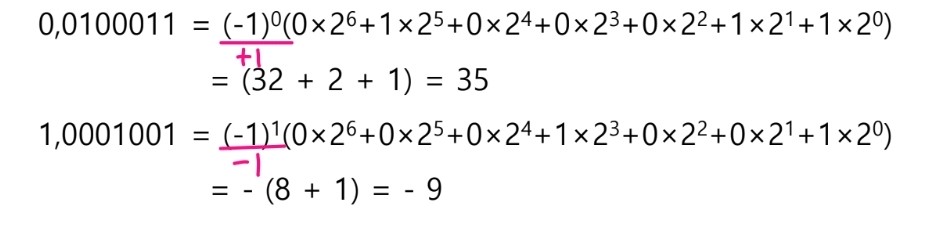
결점

• 덧셈과 뺄셈을 수행하기 위해서는 부호비트와 크기 부분을 별도로 처리해야한다.
• 0에 대한 표현이 2개 존재한다.
  

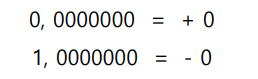
② 1의 보수 표현

개념

• 모든 비트들을 반전시킨다. (0 -> 1, 1 -> 0)

③ 2의 보수 표현

개념

• 모든 비트들을 반전하고(1의 보수를 취한 후) 결과값에 1을 더한다.
  

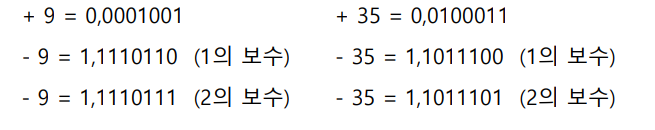
비트 확장

개념

• 데이터를 더 많은 비트의 레지스터에 저장하거나 더 긴 데이터와의 연산을 수행하기 위해 비트 확장을 수행한다.

구현 방식

• 절대치 표현의 경우 : 부호 비트를 맨좌측 위치로 이동시키고, 그 외의 비트들은 0으로 채운다.
  • 0을 추가하여 비트 확장
    

• 2의 보수에 대한 비트 확장 (=부호 비트 확장) : 확장되는 상위 비트들을 부호 비트와 같은 값으로 세트
  • 해당 부호로 비트 확장
    

▷ 부동 소수점 표현⭐

개념

• 소수부와 지수부를 두는 실수 형태의 데이터를 표현하는 방식을 말한다.
• 가수부는 소수부로서의 수치를 나타내는 부분(실제 갖고있는 값)을 말한다.

구현 방식

• 기수는 10진수에선 10으로 2진수에선 2로 고정
  

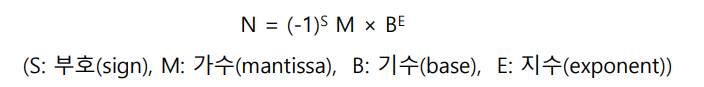
• 예를 들면 2.45 x 10² 일 때, 가수 M = 2.45, 지수 E = +2, 기수 B = 10

⭐정규화

• 부동 소수점 표현은 같은 수에 대한 부동 소수점 표현이 여러개 존재한다.
  

• 따라서 수에 대한 표현을 통일하기 위해 정규화를 사용한다.

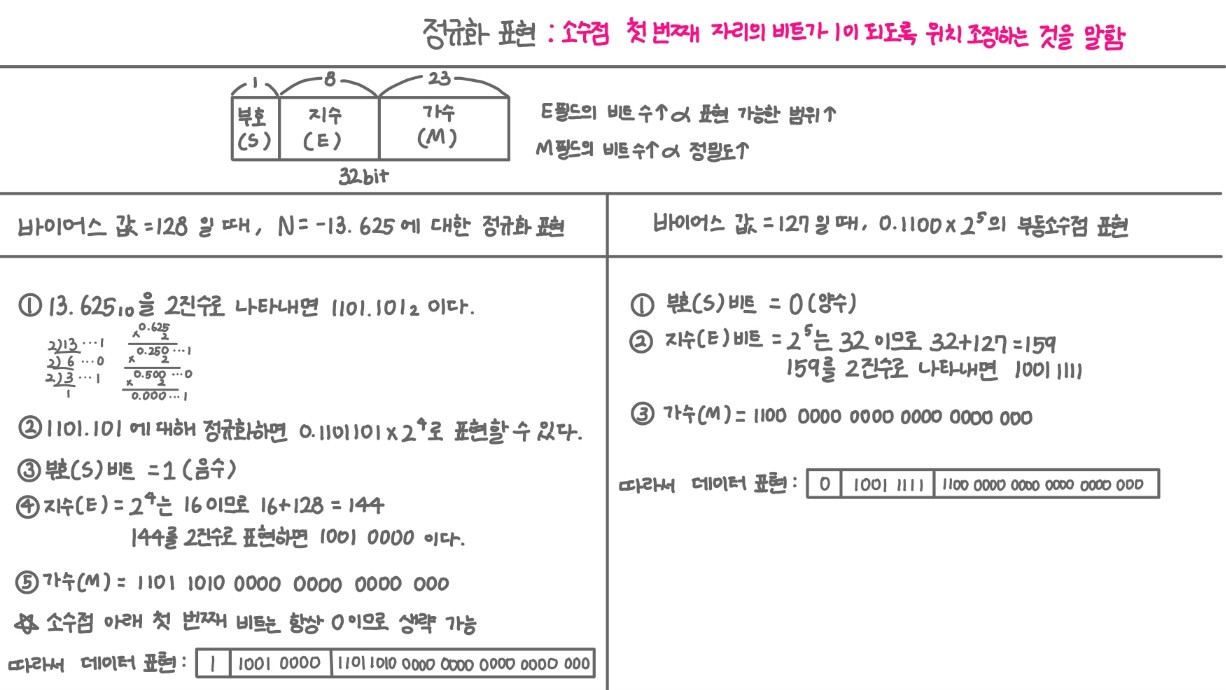
• 정규화란 가수부와 지수부를 조정하는 것을 말하며, 정규화된 표현이란 소수점 첫 번째 자리의 비트가 1이 되도록 위치 조정하는 것을 말한다.
  

정밀도

• 일반적인 32비트 부동소수점 형식은 아래와 같다. (S는 부호비트)
• 지수(E) 필드의 비트 수가 늘어나면, 표현 가능한 수의 범위 확장
  가수(M) 필드의 비트 수가 늘어나면, 정밀도 증가
  

• 정규화를 적용한 비트 배열의 예시
  • 소수점 아래 첫 번째 비트는 항상 1이므로 반드시 저장할 필요 X -> 따라서 1을 생략
    

• 바이어스된 지수
  • 음수인 지수를 표현하기 위한 방법이며, 음수 ( - )를 갖는 지수를 양( + ) 의 방향으로 편향시킨 다음에 연산을 수행하는 것을 말한다.

• 바이어스된 지수 예시(IEEE754 방식에 의함 : 부동소수점 표현을 표준화 한 것)
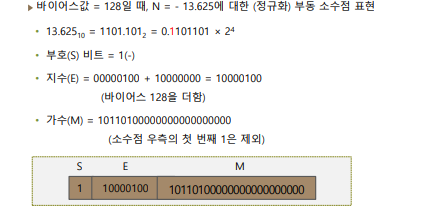
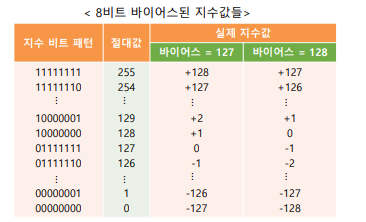
  • 바이어스값이 128이면 128을 더한 후 나중에 결과값에서 그만큼 다시 뺀다.
    

▷ 고정 소수점 표현

소수점 위치가 특수한 자리에 고정되어 있는 방식

---

▶ 논리 연산

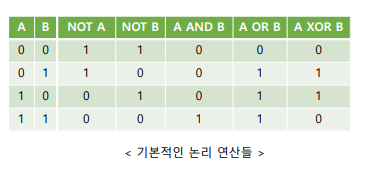
▼ AND 연산

• 두 비트들 중 하나라도 1이 아니면 0
• AND 연산은 원하는 비트들을 해당 비트에 선택적으로 바꾸고(Clear) 싶을 때 사용
  필요 없는부분을 지우는 것을 마스크(mask) 한다고 한다.
  • 아래 사진 연산 결과에서 하위 4비트가 mask
    

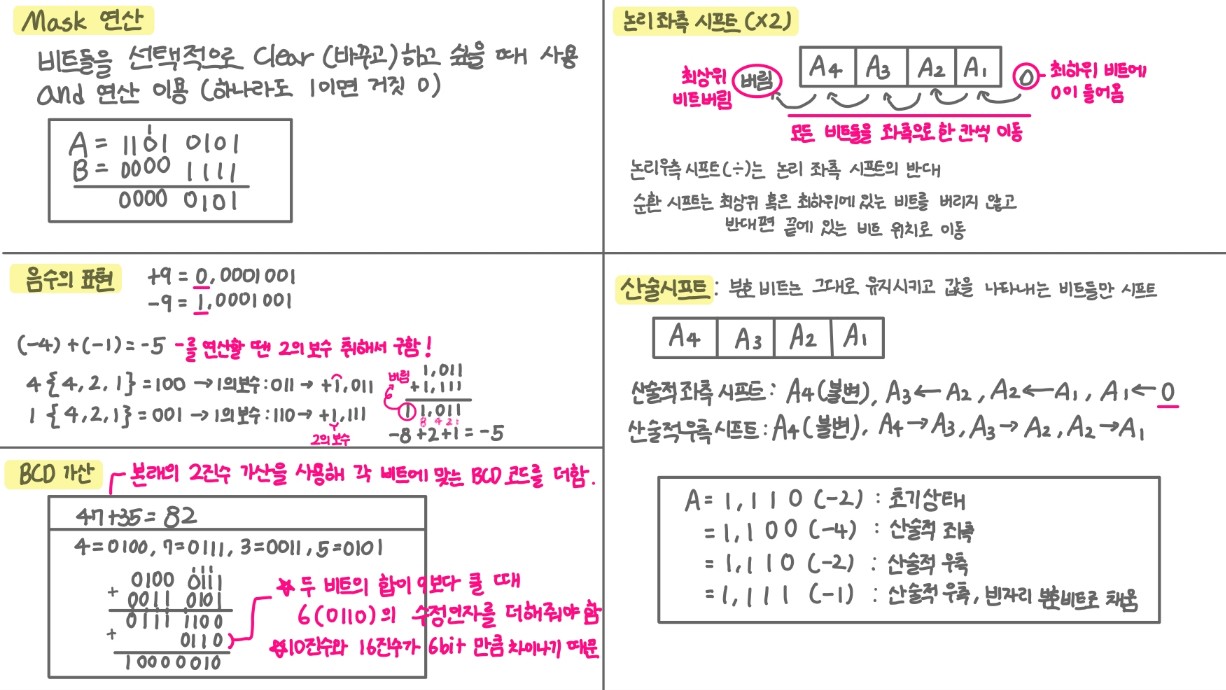
▷ Mask 연산

• 레지스터의 비트들 중에서 값이 0인 비트들과 같은 위치에 있는 A 레지스터의 비트들을 0으로 바꾸는(Clear하는) 연산
  

▷ OR 연산

• 두 비트들 중 하나라도 1이면 1
  

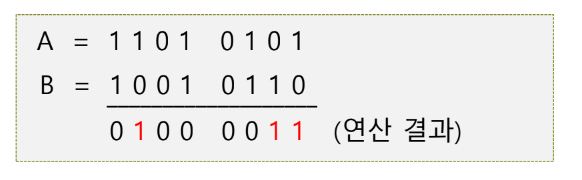
▼ XOR 연산

• 두 비트들이 다른 값을 가지면 1, 같은 값을 가지면 0
• AC 내용을 모두 지우고 싶을 때도 사용
  

▷ 선택적 - 보수 연산

• B 레지스터의 비트들 중에서 1로 세트 된 비트들에 대응되는 A 레지스터의 비트들을 보수로 변환
  

▷ 선택적 - 세트 연산

• B 레지스터의 비트들 중에서 1로 세트 된 비트들에 대응되는 A 레지스터의 비트들을 보수로 변환
  

▷ 비교(Compare) 연산

• A와 B 레지스터의 내용을 비교 → XOR 연산을 통함
• 만약 대응되는 비트들의 값이 같으면, A 레지스터의 해당 비트를 0세트
• 만약 서로 다르면, A 레지스터의 해당 비트를 1세트
  

▷ NOT 연산

• 데이터 단어의 모든 비트들을 반전(Invert)
• 1의 보수를 얻고자 할 때 쓰임
  

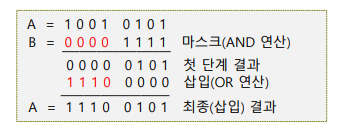
▷ 삽입(Insert) 연산

• 비트 안에서 특정 위치에 새로운 데이터를 삽입하는 방법
• 두 단계로 이루어짐
  1. 삽입할 비트 위치들에 대하여 마스크(AND) 연산 수행
  2. 새로 삽입할 비트들과 OR 연산을 수행
     

---

▶ 시프트 연산

▷ 논리 시프트

개념

레지스터 내의 데이터 비트들을 왼쪽 혹은 오른쪽으로 한 칸씩 이동하고자 할 때 쓰임

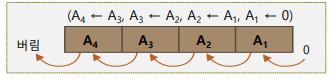
• 논리 좌측 시프트(Left Shift) X2
  • 모든 비트들을 좌측으로 한 칸씩 이동
  • 최하위 비트(A1)로는 0이 들어오고, 최상위 비트(A4)는 버림
  • ex. 레지스터8(1000) 좌측 시프트 : 8(1000)
    

• 논리 우측 시프트(Right Shift) /2
  • 모든 비트들을 우측으로 한 칸씩 이동
  • 최상위 비트(A4)로 0이 들어오고, 최하위 비트(A0)는 버림
  • ex. 레지스터8(1000) 우측 시프트: 4(0100)

▷ 순환 시프트

개념

• 최상위 혹은 최하위에 있는 비트를 버리지 않고 반대편 끝에 있는 비트 위치로 이동
• 즉, 값을 버리지 않고 원래 갖고 있던 값에서 시프트 연산 수행한다.

• 순환 좌측 시프트 (Circular Shift-Left)
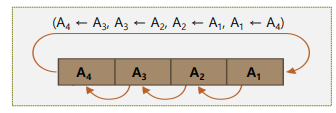
  • 최상위 비트인 A4가 최하위 비트 위치인 A1으로 이동
    

• 순환 우측 시프트 (Circular Shift-Right)
  

▷ 산술 시프트

개념

• 부호 비트는 그대로 유지시키고, 수의 크기(값)를 나타내는 비트들만 시프트

• 산술적 좌측 시프트 (Arithmetic Shift-Left)
  

• 산술적 우측 시프트(Arithmetic Shift-Right)
  

예시

• 산술 시프트에서는 외부로부터 0의 입력이 들어오지 않아 우측 시프트를 계속 수행하게 되면 빈자리가 생기는데, 빈자리에 있는 비트는 부호 비트로 채운다.
  

---

▶ 산술 연산

기본적인 산술 연산들

▷ 2의 보수 체계에서의 가산

• 두 수를 더하고, 만약 올림수(Carry)가 발생하면 버린다.
• ( - )는 보수를 취한 후 연산을 수행한다.
  

덧셈 오버플로우

• 덧셈 결과가 그 범위를 초과하여 결과값이 틀리게 될 때 오버플로우 발생
• 검출 방법 : 두 올림수(Carry)들 간의 XOR를 이용한다.
  

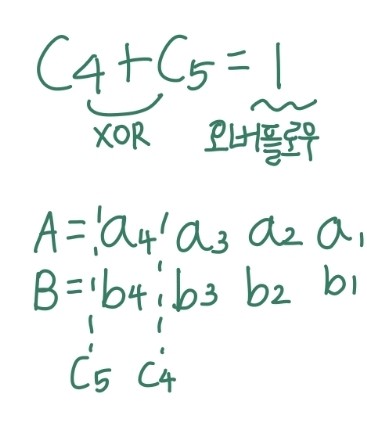
• 위에서a4 a3 a2 a1 + b4 b3 b2 b1에서 C4는 a3와 b3의 올림수를 말한다.
• 오버플로우는 ‘수의 표시 범위’에서 4비트로는 -8에서 +7 이상을 표현할 수 없기 때문에 발생하는 현상이다.

• 오버플로우 검출 방법

▷ 2의 보수 체계에서의 감산

• 덧셈을 이용하여 수행한다.
• 빼기를 플러스로 바꿔주고, 뒤에 있는 감수에 보수를 취해준다.
  

뺄셈 오버플로우

• 뺄셈 결과가 그 범위를 초과하여 결과값이 틀릭 될 때 오버플로우 발생

• 오버플로우 검출 방법(덧셈과 동일)
  

▷ BCD 가산

• 본래의 2진수 가산을 사용하여, 각 비트에 맞는 BCD 코드를 더한다.
• 두 비트의 합이 9보다 클 때 6(0110)의 수정 인자를 추가로 더해주어한다.
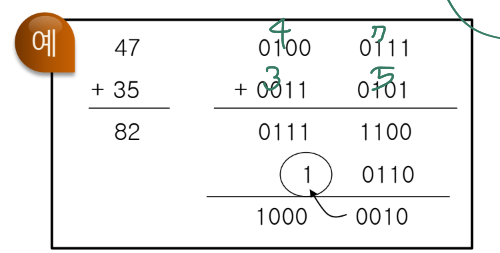
  • 10진수와 16진수가 6비트만큼 차이나기 때문
    

---

🔖정리

---

📎참조

• 『 성결대학교 김자원 교수님 』 - 컴퓨터 구조 (2023)
• 『 컴퓨터구조(제5판) 』 - 복두 출판사