우선순위 큐(Priority Queue)

이 글에서는 다음과 같은 내용을 알아봅니다.
1. Priority Queue와 Heap의 개념
2. 알고리즘에서 쓰이는 Priority Queue

우선순위 큐 (Priority Queue)

• 각 요소가 우선순위를 가지고 우선순위가 높은 요소가 먼저 나가는 구조를 가지는 추상자료형입니다.

• 단순하게 우선순위에 따라 요소가 먼저 나가는 형태를 '우선순위 큐'라고 부르기로 정의한 것이고 세부적인 구현을 정의한 개념은 아닙니다. 따라서 우선순위 큐는 자료구조(Data Structure)가 아닌 추상자료형(ADT)입니다.

• 세부적인 구현은 대부분 힙(heap) 자료구조로 구현됩니다. java의 PriorityQueue 또한 힙으로 구현되어있습니다.
  
  

힙 (heap)

• 우선순위를 가진 노드로 구성된 완전 이진 트리로, 부모 노드의 우선순위가 자식 노드의 우선순위보다 높게 유지되는 자료구조입니다.
  

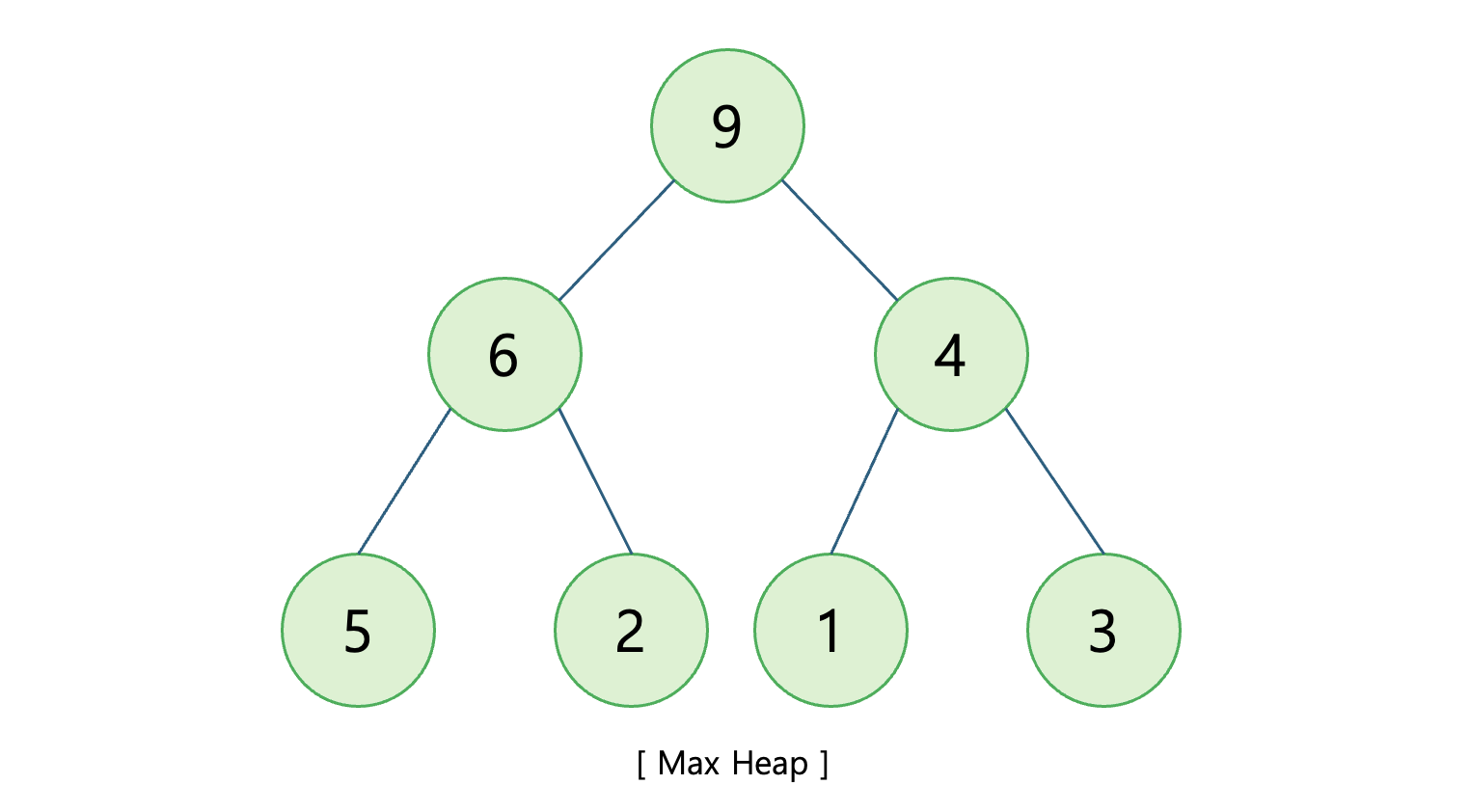
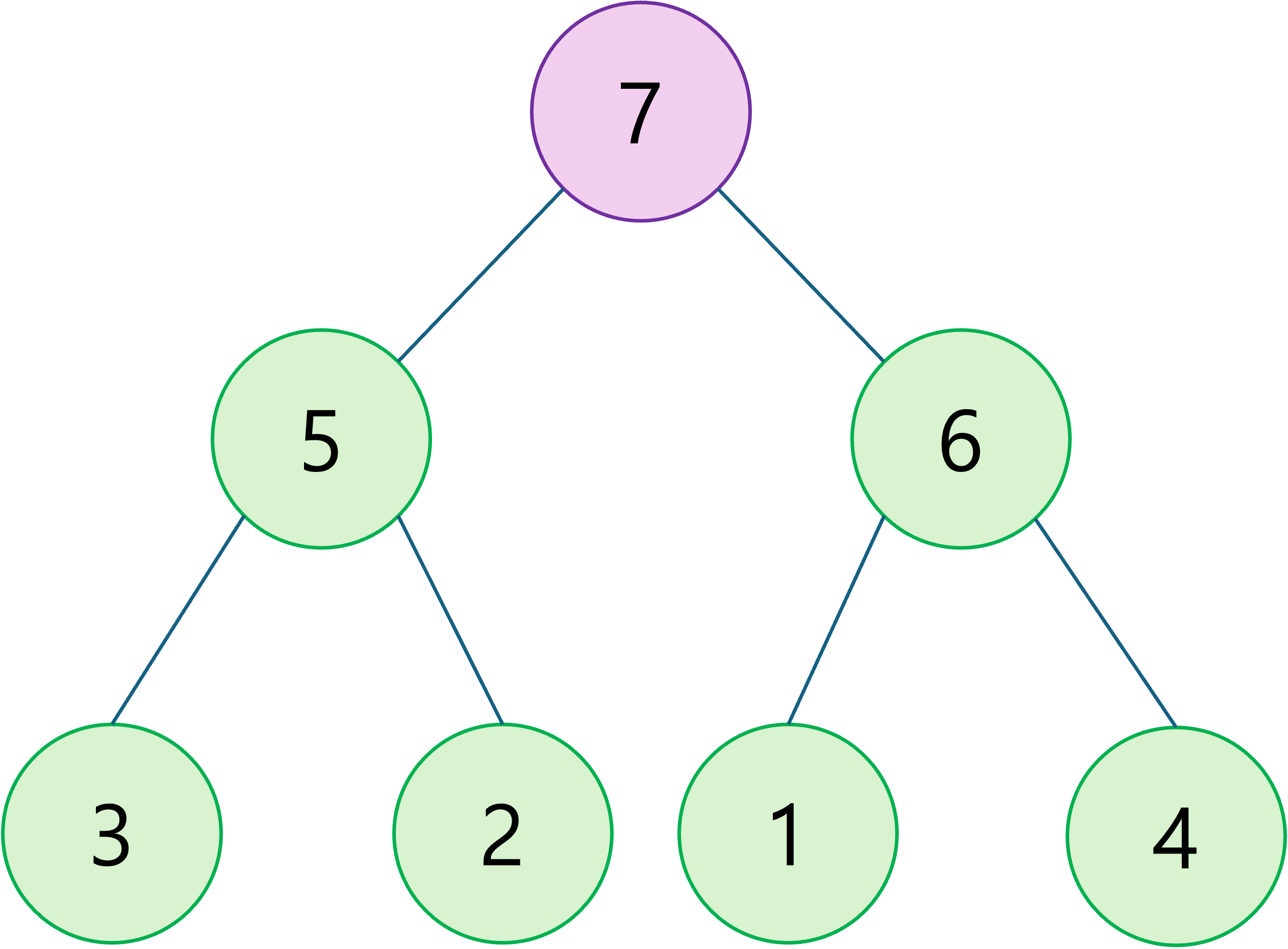
• 위 그림은 '노드의 값이 높을 수록 우선 순위가 높다'는 기준을 적용한 힙입니다.

• 힙의 정의에 따라 부모 노드의 값이 자식 노드보다 항상 크다는 것을 확인할 수 있습니다. 루트 노드는 모든 노드의 최고 조상이므로 가장 값이 크다는 특징이 있습니다. 이러한 특징을 가지는 자료구조를 힙 중에서도 '최대 힙(Max Heap)'이라고 부릅니다.

• 반대로 '노드의 값이 낮을 수록 우선 순위가 높다'는 기준을 적용한 힙은 '최소 힙(Min Heap)'이라 부릅니다.
  
  

힙 연산 - 삭제

• 힙에서의 데이터 삭제는 루트노드의 데이터를 삭제하는 것을 의미합니다. 즉, 우선순위가 가장 높은 데이터를 삭제하는 것입니다.
• 루트노드를 삭제한 후 힙의 마지막 요소를 루트로 옮깁니다. 그리고 힙 속성을 유지하기 위해 아래로 내려가며 우선순위가 높은 자식 노드와 위치를 바꿉니다.
• 위에서 보여드린 Max Heap을 예시로 힙의 데이터 삭제과정을 보여드리면 다음과 같습니다.

1. 루트노드 삭제
   

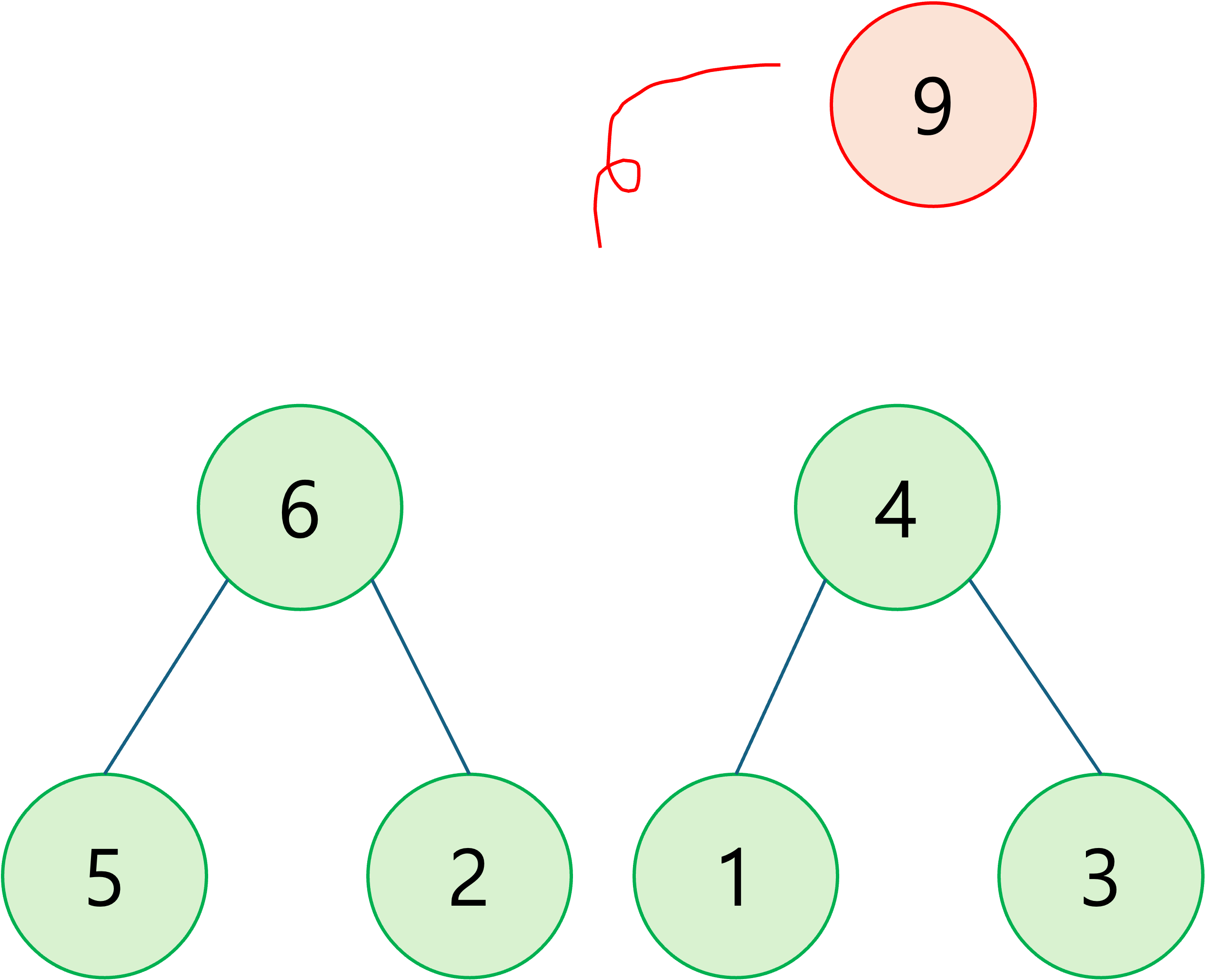
2. 가장 마지막 요소를 루트로 옮긴다.
   

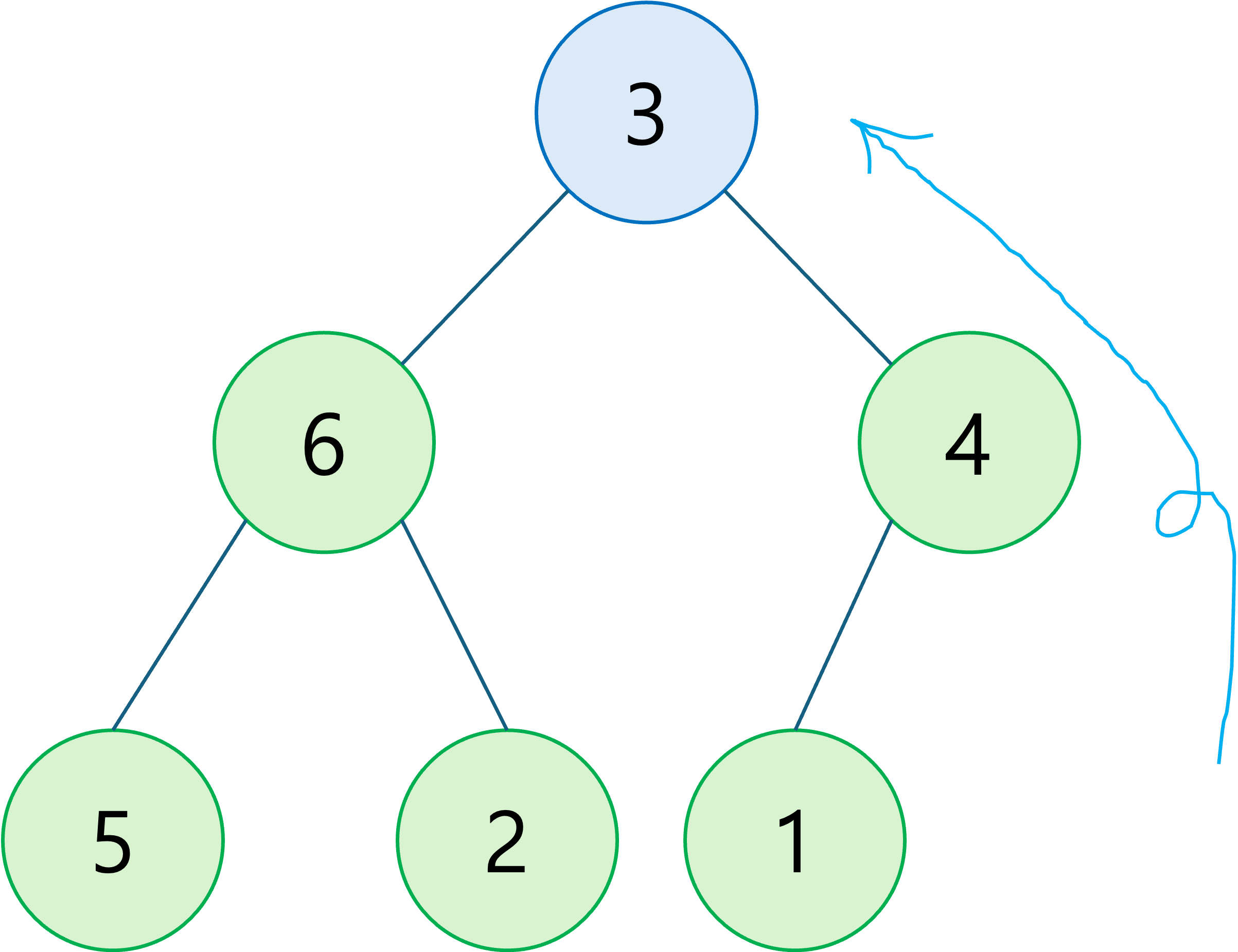
3. 우선순위가 높은 자식이 있다면 위치를 바꾼다. (두 자식 노드가 모두 우선순위가 높다면, 둘 중에 우선순위가 더 높은 자식과 위치를 바꾼다.)
   

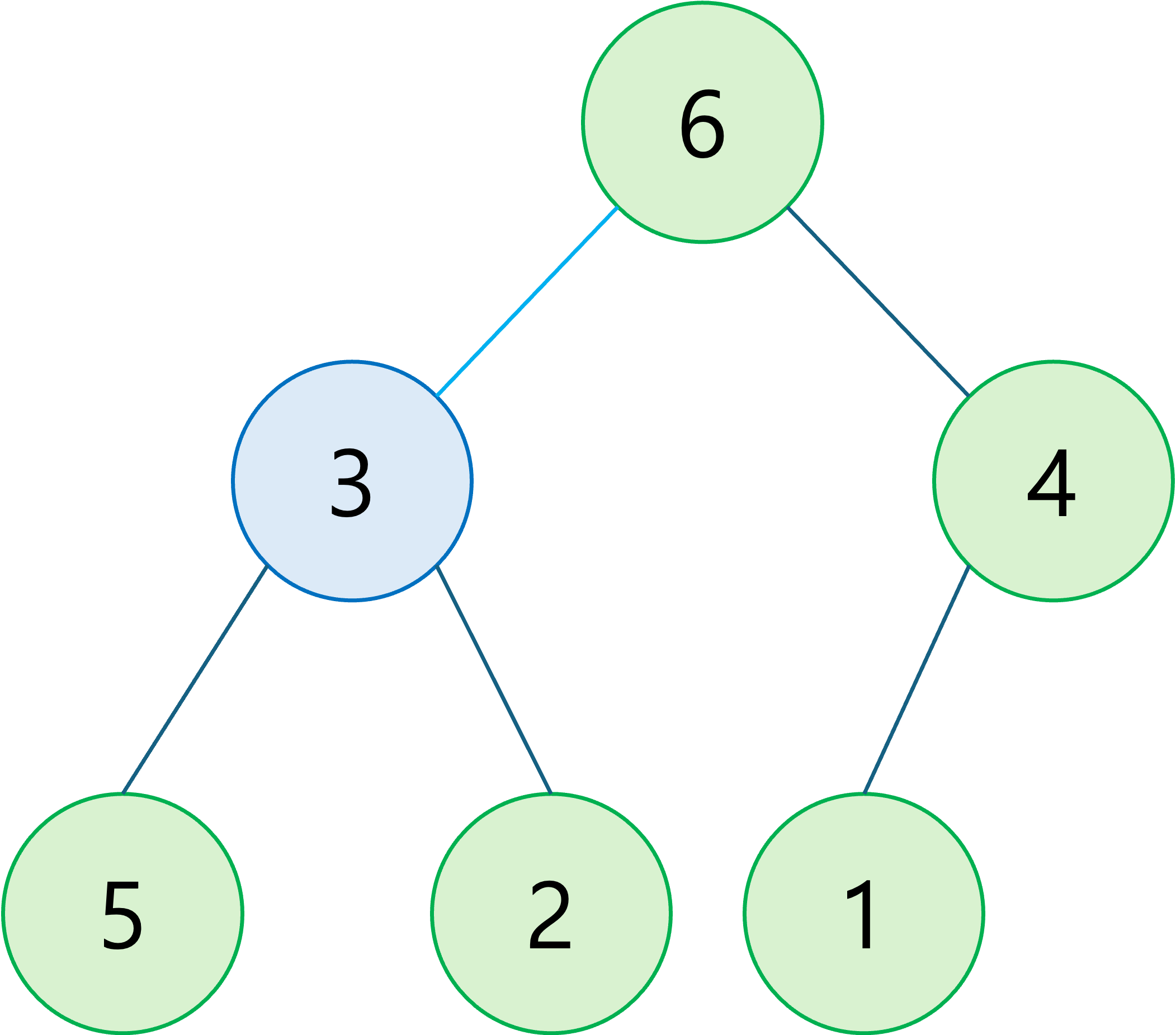
4. 우선순위가 높은 자식이 없을 때까지 반복한다.
   

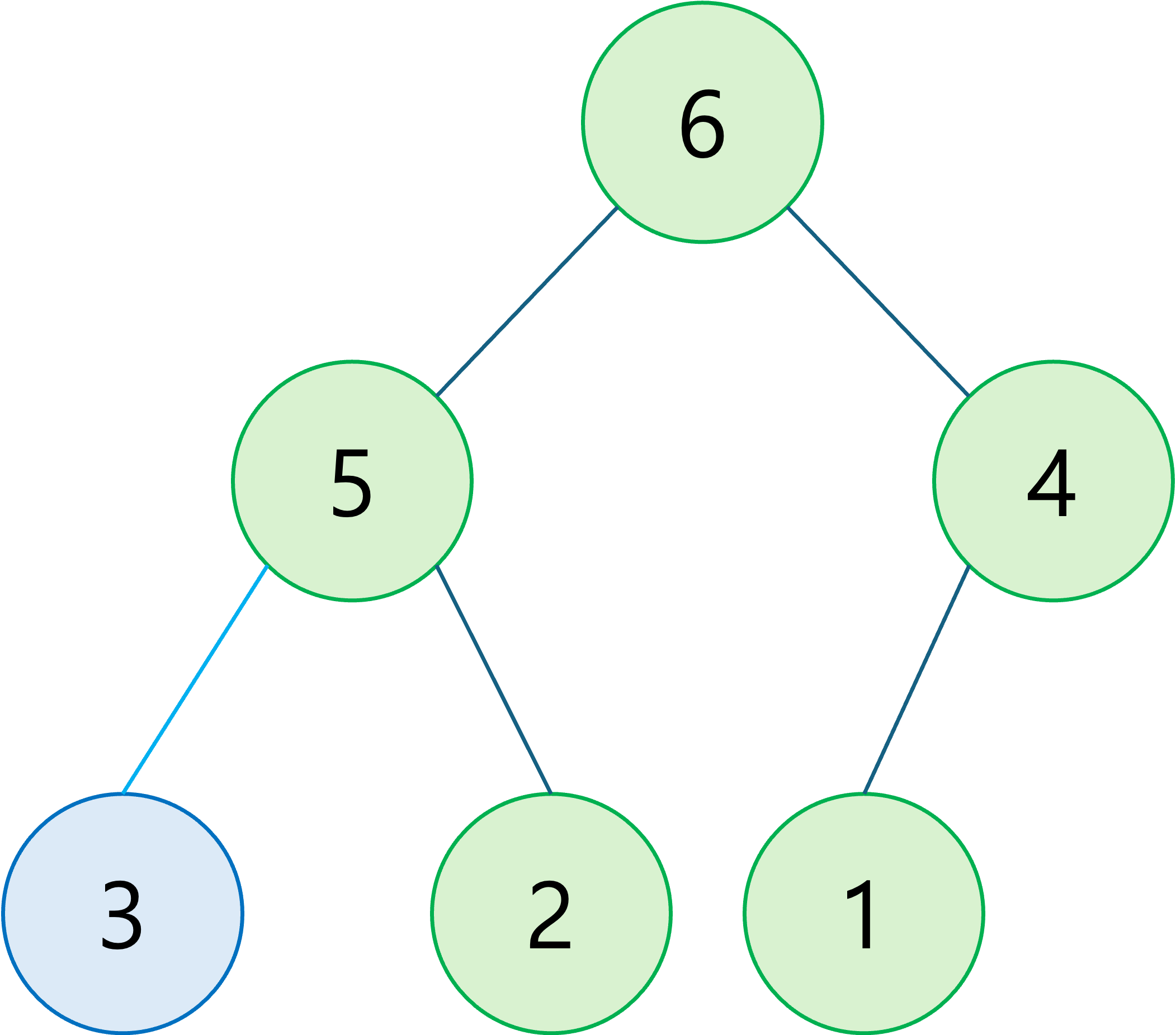
삭제가 완료되었습니다. 삭제 연산 전 후의 모습은 다음과 같습니다.

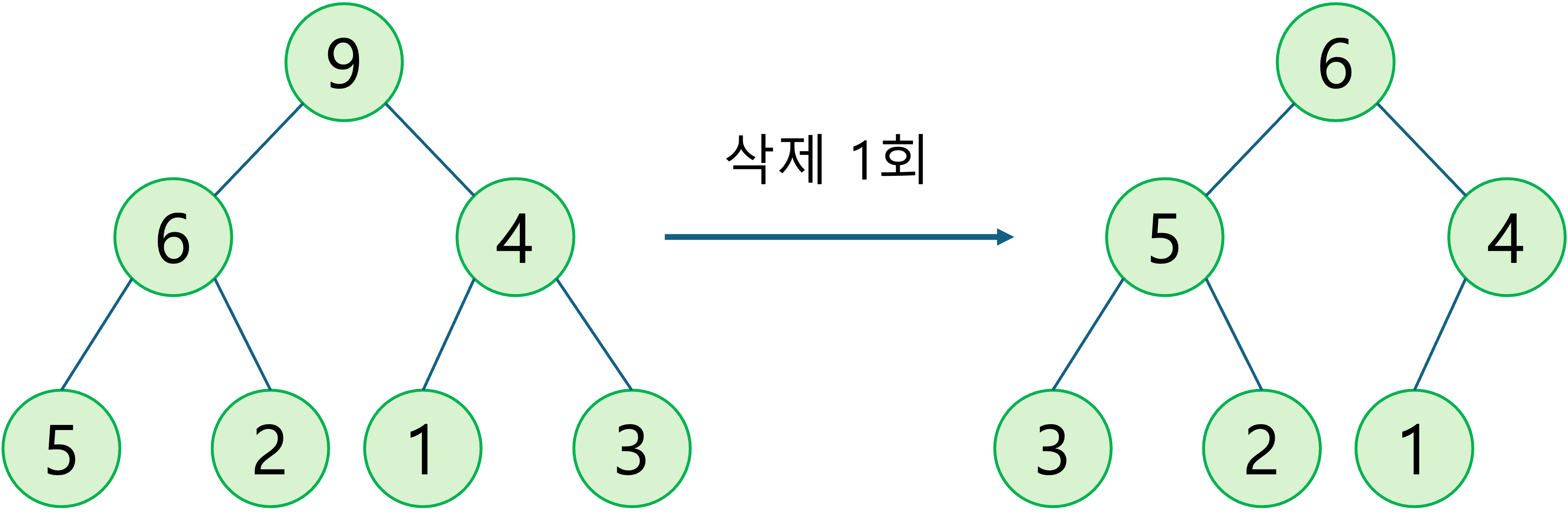
힙 연산 - 삽입

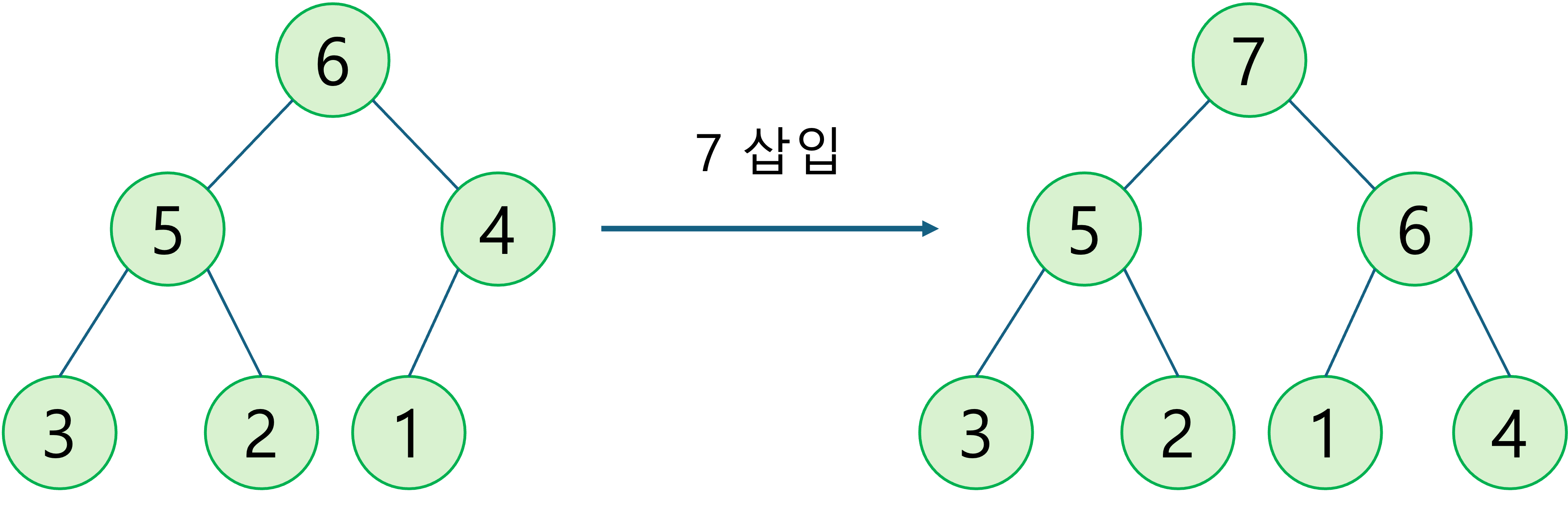
• 새 요소를 힙의 마지막에 추가한 후, 힙 속성을 유지하기 위해 위로 올라가며 우선순위가 낮은 부모 노드와의 위치를 바꿉니다.
• 삽입 과정을 보여드리면 다음과 같습니다.

1. 마지막 위치에 새 요소 삽입
   

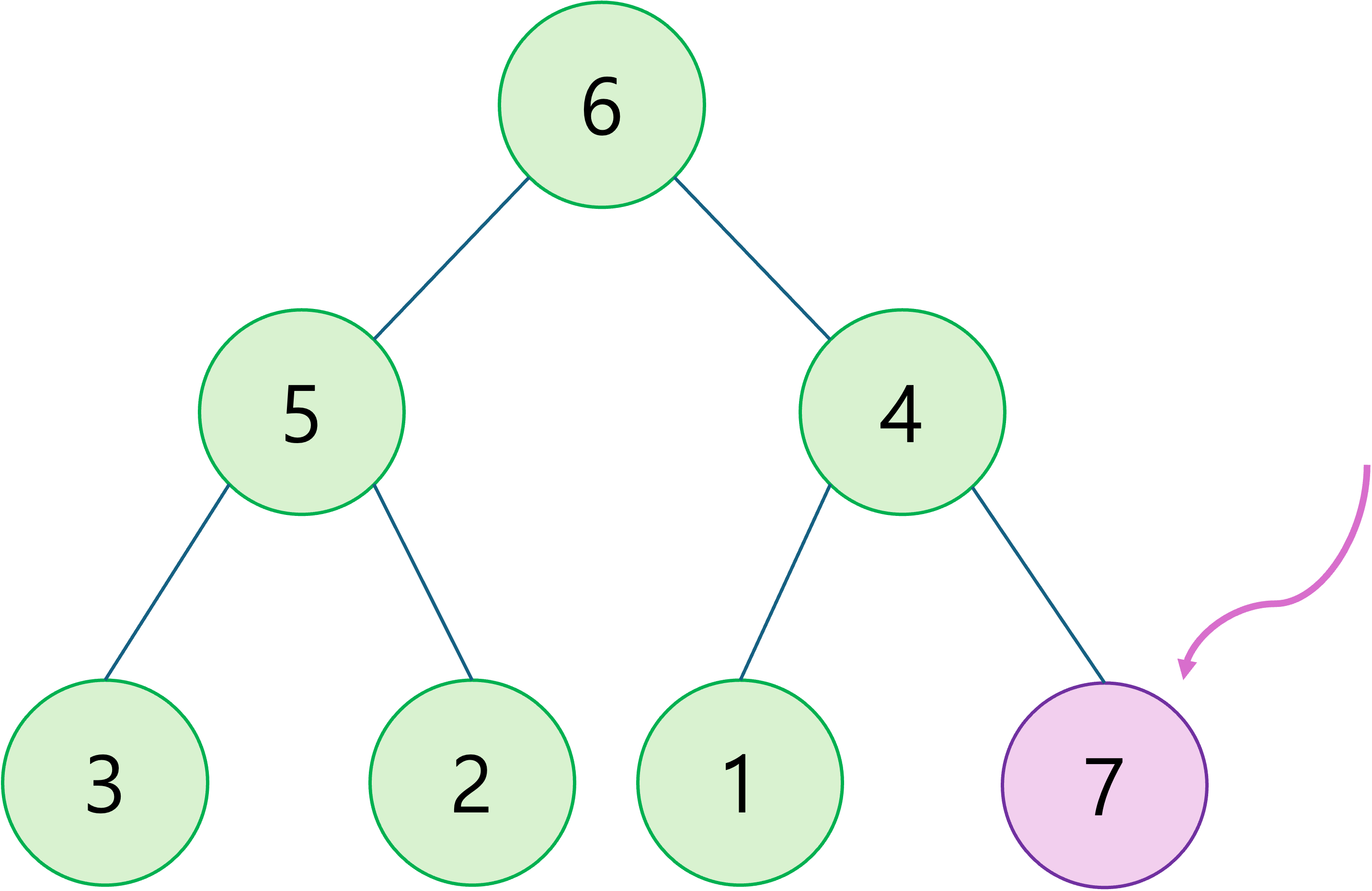
2. 부모가 우선순위가 낮다면, 부모와 자리를 바꾼다.
   

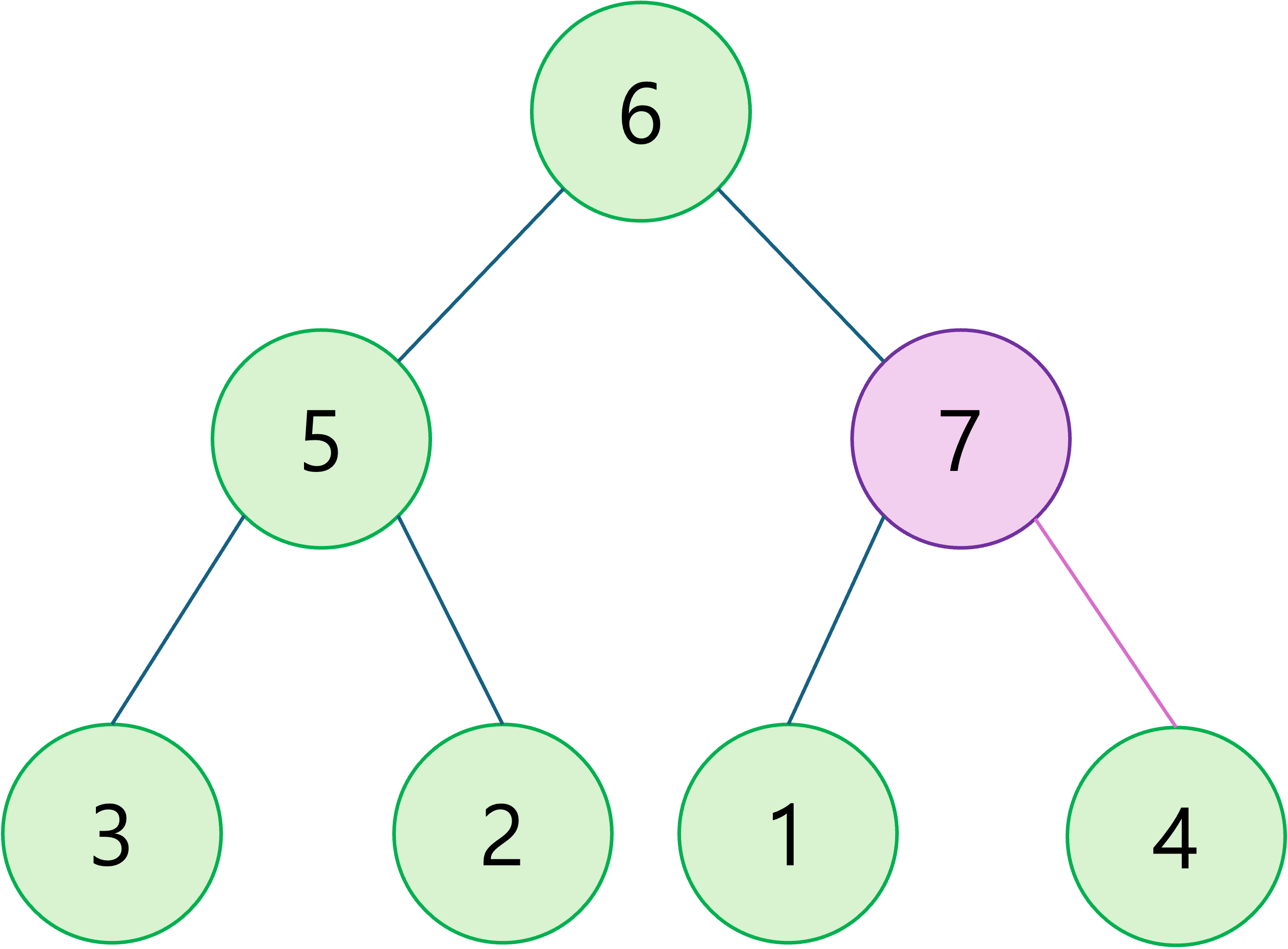
3. 부모가 우선순위가 높을 때까지 반복한다.
   

삽입이 완료되었습니다. 삽입 연산 전 후의 모습은 다음과 같습니다.

힙 연산의 복잡도: $O(log N)$

• 힙에서 루트를 삭제 후, 마지막 요소가 제자리를 찾을 때까지 내려가는 최악의 경우는 힙의 높이만큼입니다.

• 힙에서 요소를 삽입 후 삽입된 요소가 제자리를 찾을 때까지 올라가는 최악의 경우는 힙의 높이만큼입니다.

• 힙의 높이를 $x$라고 했을 때 삽입, 삭제 모두 $O(x)$의 시간 복잡도를 가진다는 것입니다. 이를 데이터의 크기인 $N$에 관한 식으로 바꾸기 위해 높이가 $x$인 완전 이진트리를 생각해봅시다.
  

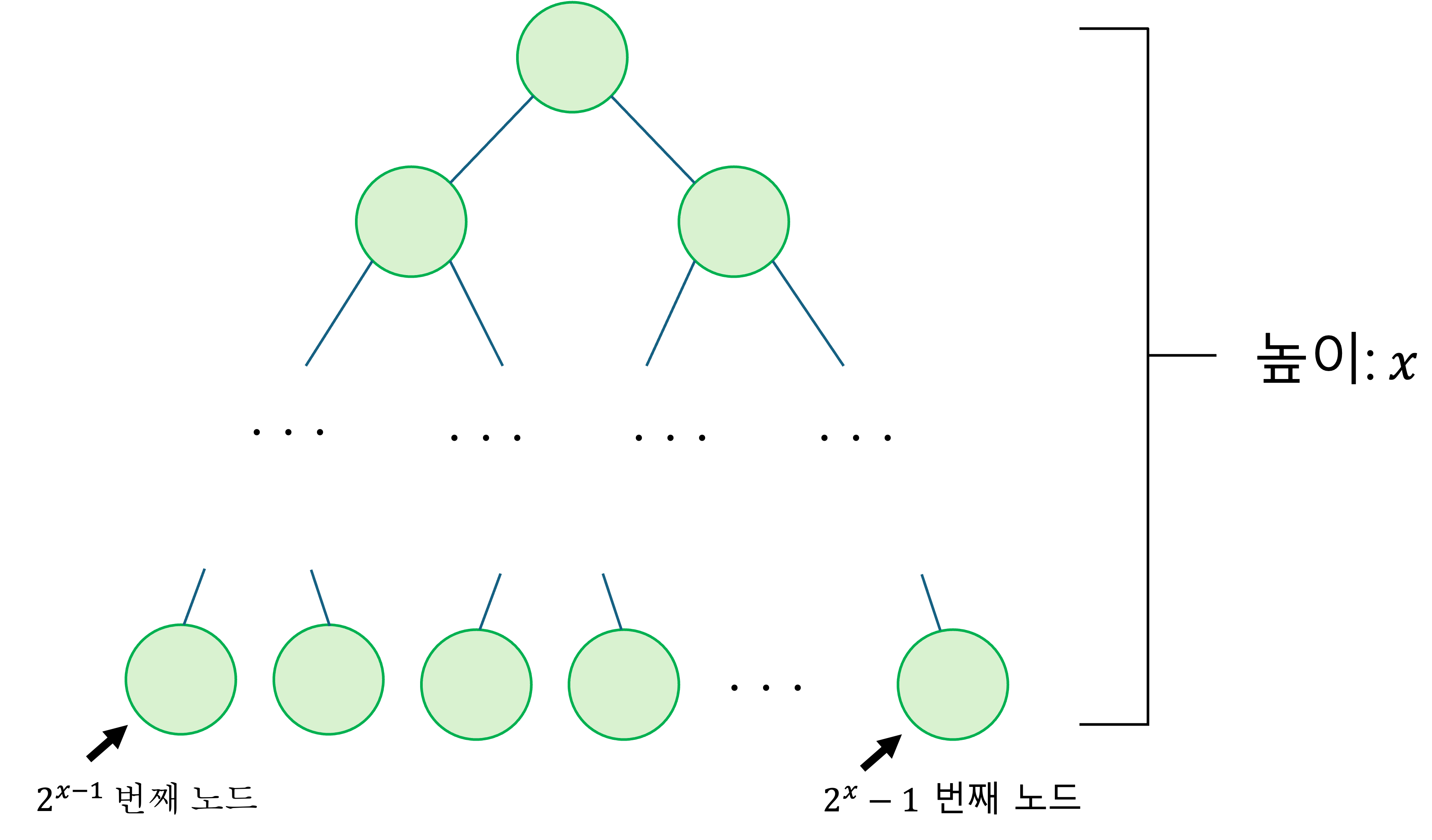
• 노드 개수를 $N$이라 할 때, 완전 이진 트리에서 $x$와 $N$의 관계는 다음과 같습니다.
  $2^{x-1} ≤ N ≤ 2^x - 1$

• 양 변에 $log_2$를 취하면
  $x-1 ≤ log_2{N} ≤ log_2{(2^x-1)} < log_2{2^x} = x$

• 위 관계를 통해 $x$는 다음과 같은 부등식을 유도할 수 있습니다.
  $log_2{N} < x ≤ log_2{N} + 1$
  
  

• $N→∞$일 때, $x→log_2{N}$ 이고 $O(x) = O(log{N})$ 임을 알 수 있습니다.
  
  
  

PriorityQueue와 힙

• 자바에서 우선순위 큐를 구현한 PriorityQueue 클래스는 heap으로 구현되어있으므로 PriorityQueue의 삽입, 삭제 연산또한 $O(logN)$ 시간복잡도를 가집니다.
• 자바 뿐만이 아니라 대부분의 언어에서 PriorityQueue는 heap을 사용해 구현되어있습니다.
  
  

PriorityQueue 는 언제 사용할까?

• 데이터 셋이 지속적으로 변하는 상황에서 우선순위에 따라 처리하고 싶을 때 사용합니다.

[ Priority Queue 사용 상황 예시 ]
모든 환자를 1시간만에 치료하는 병원이 있습니다. 이 병원에서는 환자의 긴급도에 따라 우선순위를 할당하고, 가장 긴급한 환자를 먼저 치료하고자 합니다. 현재 병원에서 치료를 기다리고있는 환자는 3명이며 각각의 긴급도는 5, 10, 7 입니다. 그런데 인근에 사고가 발생하여 몇 명의 환자가 더 병원에 도착하기로 했습니다. 도착 정보는 다음과 같습니다.

```
1시간 뒤에 긴급도 6의 환자가 도착합니다.
2시간 뒤에 긴급도 9의 환자가 도착합니다.
3시간 뒤에 긴급도 8의 환자가 도착합니다.
```

시간이 지남에 따라 환자의 긴급도가 변하지 않는다 가정했을 때, 치료되는 환자의 긴급도 순서는 어떻게 되는가?

• 만약 치료해야할 6명의 환자가 모두 병원에서 대기중이었다면(=데이터 셋이 변하지 않는 상황이라면) 환자의 긴급도를 내림차순으로 정렬하여 순차적으로 처리하는 것이 훨씬 효율적이고 직관적입니다.
  => 5, 10, 7, 6, 9, 8 을 정렬
  => 10, 9, 8, 7, 6, 5 순으로 치료된다.
  
  
• 하지만 위 상황에서는 3번에 거쳐 1시간마다 새로운 환자가 유입되므로 매 시간마다 치료되는 환자, 유입되는 환자를 고려해 우선순위가 가장 높은 환자를 다시 판단해야합니다.
  => 10 환자 치료, 6 환자 도착하여 7, 6, 5 대기중
  => 7 환자 치료, 9 환자 도착하여 9, 6, 5 대기중
  => 9 환자 치료, 8 환자 도착하여 8, 6, 5 대기중
  => 결론적으로 10, 7, 9, 8, 6, 5 순으로 치료된다.
  
  
• 대기중인 환자 리스트를 매 시간 데이터가 변할 때마다 정렬한다면 매우 부담스러운 작업이 될 것입니다. 위 예시에서는 정렬해야할 원소의 개수가 3개밖에 되지 않지만 만약 10만개라면? 100만개라면..?? heap으로 구현된 PriorityQueue를 쓰는 것이 최선일 것입니다.
  
  

  결론: 알고리즘을 풀이하다 지속적으로 변하는 데이터 셋, 우선 순위에 따라서 처리 두가지가 공존하는 상황을 마주한다면 'PriorityQueue를 사용하면 되겠구나!'하고 생각하면 되겠습니다.