[Java] 크루스칼 알고리즘 (Kruskal Algorithm), 최소 신장 트리 (MST)

본 글에서는
MST가 무엇인지 알아봅니다.
MST를 구하는 알고리즘인 크루스칼 알고리즘에 대해서 알아봅니다.

부분 그래프

• 어떤 그래프의 정점의 일부와 변의 일부를 사용해 만들 수 있는 그래프입니다.
• $V(X)$는 그래프 $X$의 정점의 집합, $E(X)$는 그래프 $X$의 간선의 집합을 의미할 때, $G$의 부분 그래프 $G'$는 다음을 만족합니다.

  $V(G') ⊂ V(G)$
  $E(G') ⊂ E(G)$

신장 트리 (Spanning Tree)

• 그래프의 모든 노드를 사이클 없이 연결하는 부분 그래프입니다.
• N개의 정점과 M개의 간선을 가지는 그래프 G의 신장 트리는 N개의 정점과 (N - 1)개의 간선으로 구성됩니다.

최소 신장 트리 (Minimun Spanning Tree)

• 그래프의 모든 노드를 최소 비용으로 연결하는 부분 그래프입니다.
• Minimun Spanning Tree를 줄여서 MST 라고도 부릅니다.

  최소 신장 트리(MST) ⊂ 신장 트리 ⊂ 부분 그래프

MST 활용

• 가장 적은 비용을 들여 모든 정점이 연결되어야 하는 상황에는 MST가 유용하게 사용됩니다. 실제 상황으로 예시를 들면 다음과 같은 상황이 있습니다.

1. 네트워크 설계 : 모든 네트워크 노드가 최소 비용으로 연결되도록 MST를 사용해 설계할 수 있습니다.
2. 도로 건설 계획 : 모든 집끼리 서로 연결되도록 도로를 건설할 때 최소 비용으로 도로를 건설하려 한다면 MST를 사용해 도록 건설 계획을 세울 수 있습니다.

MST 구하기

• 어떤 그래프의 MST를 구하는 알고리즘은 대표적으로 2가지가 존재합니다.

1. 크루스칼 알고리즘 → 간선을 중심으로 계산
2. 프림 알고리즘 → 정점을 중심으로 계산

• 본 글에서는 두 방법 중 크루스칼 알고리즘을 살펴보겠습니다.

크루스칼 알고리즘

• 간선을 중심으로 MST를 구하는 알고리즘입니다.
• 다음과 같은 방법으로 수행됩니다.

1. 가중치가 낮은 간선부터 순서대로 간선을 살펴본다.
2. 해당 간선이 사이클을 형성하지 않는다면 선택한다.
3. 간선을 (정점 개수 - 1)개 선택할 때까지 반복한다.

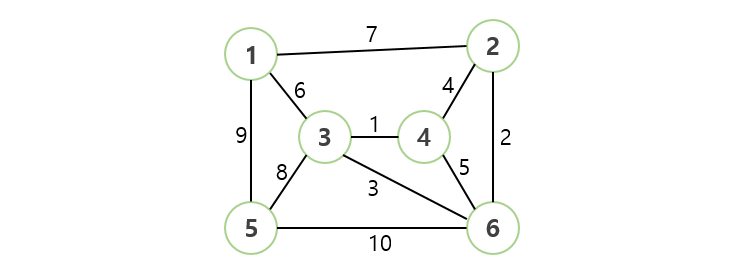
• 예시 아래 그래프의 MST를 구하는 과정입니다.
  

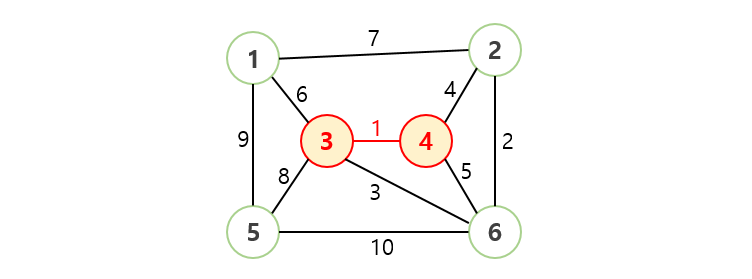
1. 가중치가 가장 낮은 간선을 선택합니다.
   

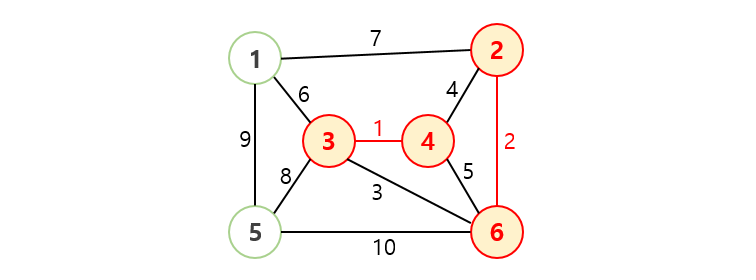
2. 다음으로 가중치가 가장 낮은 순서대로 간선을 선택합니다.
   
   

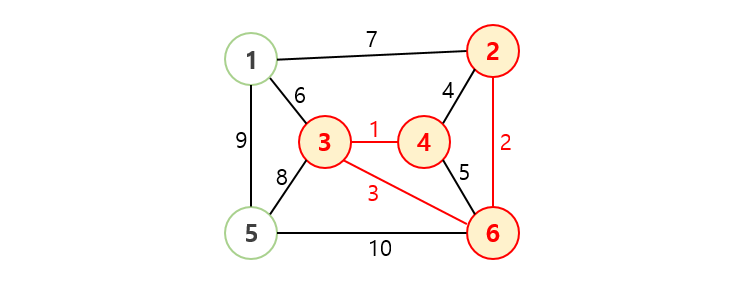
3. 그러다가 선택한 간선이 사이클을 형성하면, 선택하지 않고 건너뜁니다.
   
   

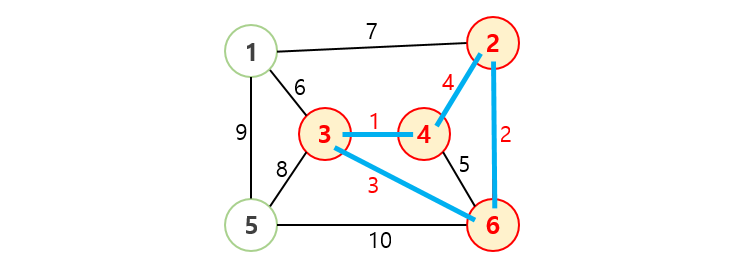
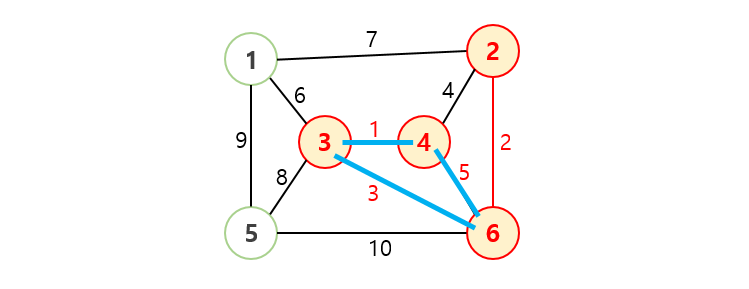
4. 위 규칙대로 간선이 (정점 개수 - 1)개 선택될 때까지 반복하면 MST가 완성됩니다.
   
   

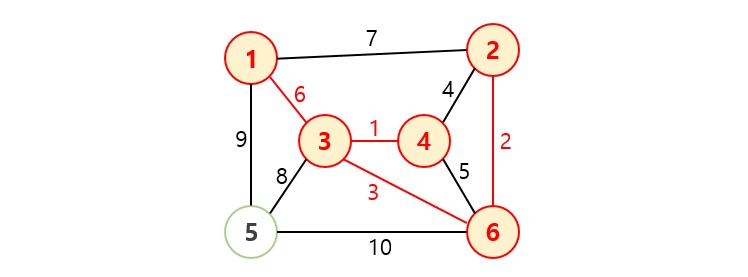
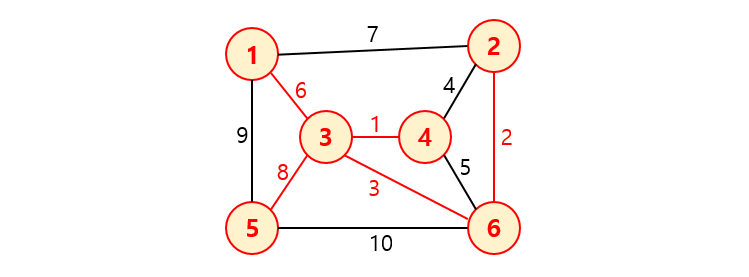
• 크루스칼 알고리즘을 통해서 구한 MST입니다.
  

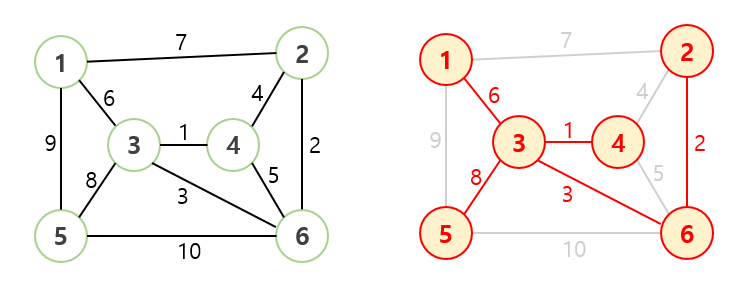
크루스칼 알고리즘 구현

• 간선 중심으로 진행되는 알고리즘이므로 그래프를 다룰 때 간선 리스트 방식을 사용합니다.

  💡 그래프 표현 방식
  1. 인접 리스트(adjacent list) : 각 정점에 연결된 정점을 리스트로 저장하는 방식
  2. 인접 행렬(adjacent metrix) : 노드간의 연결 관계를 2차원 행렬로 나타내는 방식
  3. 간선 리스트(edge list) : 그래프의 모든 간선을 [시작 노드, 종료 노드, 가중치] 형태로 리스트에 저장하는 방식

• cycle이 발생하는지 확인하기 위해 Union Find를 사용합니다.

  💡 union find란?
  https://velog.io/@signkite/union-find

import java.util.*;

class Edge {
	int v1;
	int v2;
	int weight;
	
	Edge (int v1, int v2, int weight) {
		this.v1 = v1;
		this.v2 = v2;
		this.weight = weight;
	}
}

public class Main {
	static int[] parents;  // union find 에 사용
	
	static String graph = "1 2 7\n" + // 정점1 정점2 가중치
						  "1 3 6\n" +
						  "1 5 9\n" +
						  "2 4 4\n" +
						  "2 6 2\n" +
						  "3 4 1\n" +
						  "3 5 8\n" +
						  "3 6 3\n" +
						  "4 6 5\n" +
						  "5 6 10\n";

	static List<Edge> MST = new ArrayList<>();  // 최종적으로 구할 MST의 간선 리스트 표현
	
	public static void main(String[] args) {
		
		/* 그래프 정보 입력받기 */
		Scanner sc = new Scanner(graph);
		
		List<Edge> edges = new ArrayList<>();
		for (int i = 0; i < 10; ++i) {
			int v1 = sc.nextInt();
			int v2 = sc.nextInt();
			int weight = sc.nextInt();
			
			edges.add(new Edge(v1, v2, weight));
		}
		
		/* 간선 리스트를 간선의 가중치가 작은 순서대로 정렬 */
		Collections.sort(edges, (e1, e2) -> {
			return e1.weight - e2.weight;
		});
		
		/* union find 를 사용해 사이클을 확인하기 위해 정점 집합 초기화 */
		parents = new int[7];
		for (int i = 1; i <= 6; ++i) {
			parents[i] = i;
		}
		
		/* 사이클이 발생하지 않도록 가중치가 작은 간선부터 하나씩 선택 */
		int selected = 0;
		for (Edge cur: edges) {
			
			/* 현재 간선의 양 끝점이 이미 연결되어 같은 집합에 속해있다면
			 * 현재 간선을 추가했을 때 사이클이 발생하게 되므로 건너뛴다. */
			if (find(cur.v1) == find(cur.v2))
				continue;
			
			union(cur.v1, cur.v2);
			MST.add(cur);
			
			selected++;
			
			/* (정점 수 - 1)개의 간선을 선택했다면 종료 */
			if (selected == 6 - 1)
				break;
		}
		
		/* 모든 정점이 연결되어있지 않아 MST를 만들 수 없는 경우 */
		if (selected < 6 - 1) {
			System.out.println("MST를 만들 수 없습니다.");
			return;
		}
		
		/* 완성된 MST 출력 */
		System.out.println("--- MST 완성! ---");
		int totalWeight = 0;
		for (Edge e: MST) {
			System.out.printf("v1: %d, v2: %d, weight: %d\n", e.v1, e.v2, e.weight);
			totalWeight += e.weight;
		}
		System.out.println("총 가중치: " + totalWeight);
	}
	
	/* union find 를 위한 메서드 */
	static int find(int x) {
		if (parents[x] == x)
			return x;
		
		return parents[x] = find(parents[x]);
	}
	static void union(int x, int y) {
		int rootX = find(x);
		int rootY = find(y);
		
		if (rootX != rootY)
			parents[rootX] = rootY;
	}
}

크루스칼 알고리즘의 시간 복잡도

$E$ 를 간선의 개수, $V$ 를 정점의 개수라 했을 때,

1. 간선 정렬: $O(ElogE)$
2. make: $O(V)$
3. union: 최악의 경우 모든 간선을 살피므로 $O(E)$

• 결론: $O(ElogE + V + E) = O(ElogE)$

마무리

• 오늘 최소 신장 트리가 무엇인지, 크루스칼 알고리즘을 통해 어떻게 구하는지 살펴보았습니다. 크루스칼 알고리즘을 사용하면 그래프의 모든 정점을 최소한의 비용으로 연결하는 방법을 효율적으로 알아낼 수 있습니다. 해당 알고리즘을 연습할 수 있는 알고리즘 문제를 하나 첨부하고 마무리하도록 하겠습니다.

  백준 1922 네트워크 연결
  https://www.acmicpc.net/problem/1922