UNIX 파일시스템

• Super block
  파일 시스템의 총체적 레이아웃 정보 보관
  블록의 크기, inode 수, data block 의 수, free block list 의 헤드

• inode block
  메타데이터 보관 (실제 데이터 블록의 위치 정보 포함)

• data 블록
  실제 데이터 보관

유닉스 파일 시스템에는 각 파일마다 그 파일의 메타데이터를 저장하는 아이노드 존재

---

Ext2 파일 시스템

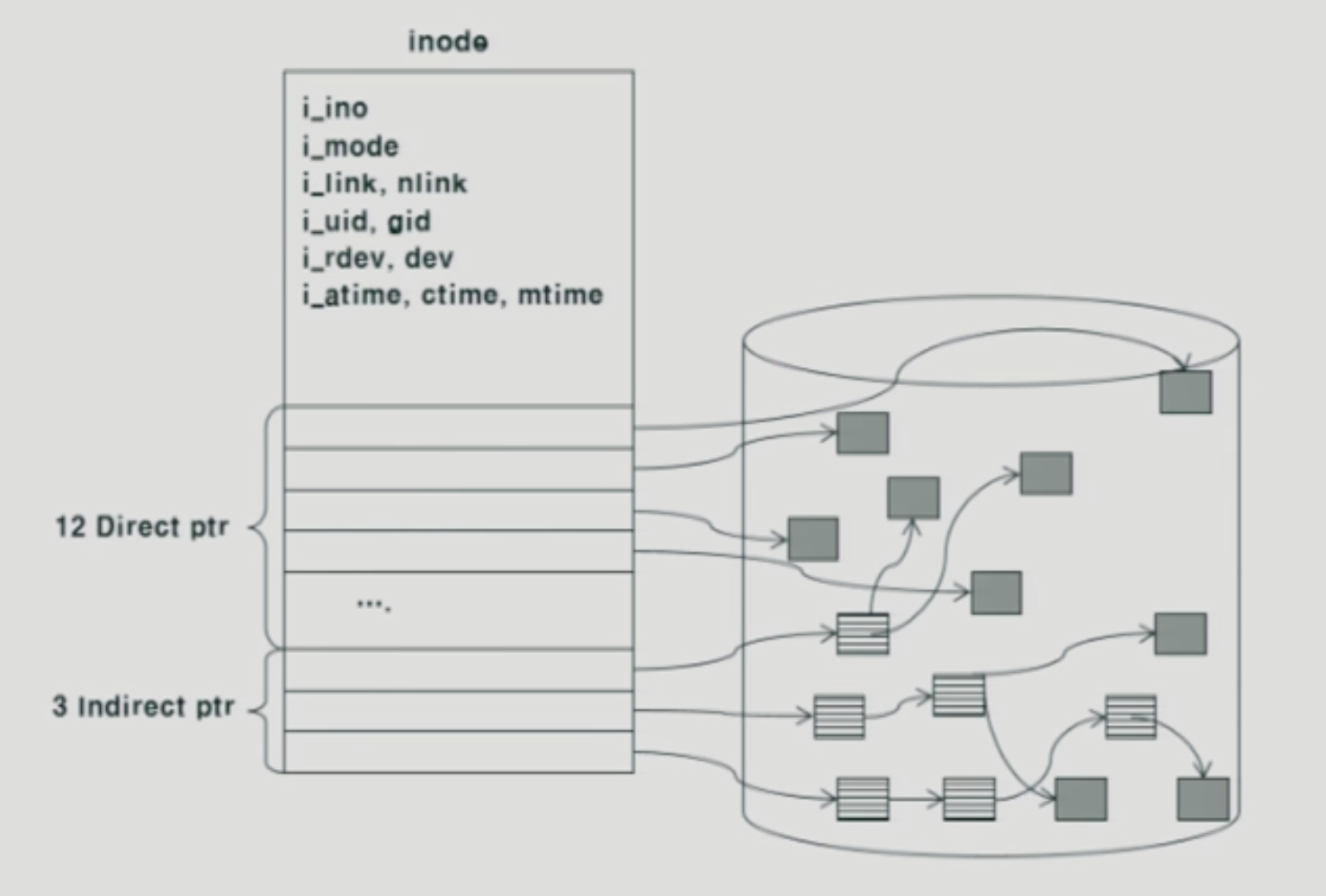
여러 메타데이터들이 아이노드 부분에 저장됨.
파일의 위치정보를 나타내는 부분이 15개의 포인터로 구성.

indirect 포인터는 대단히 큰 파일의 정보를 나타내기 위함.

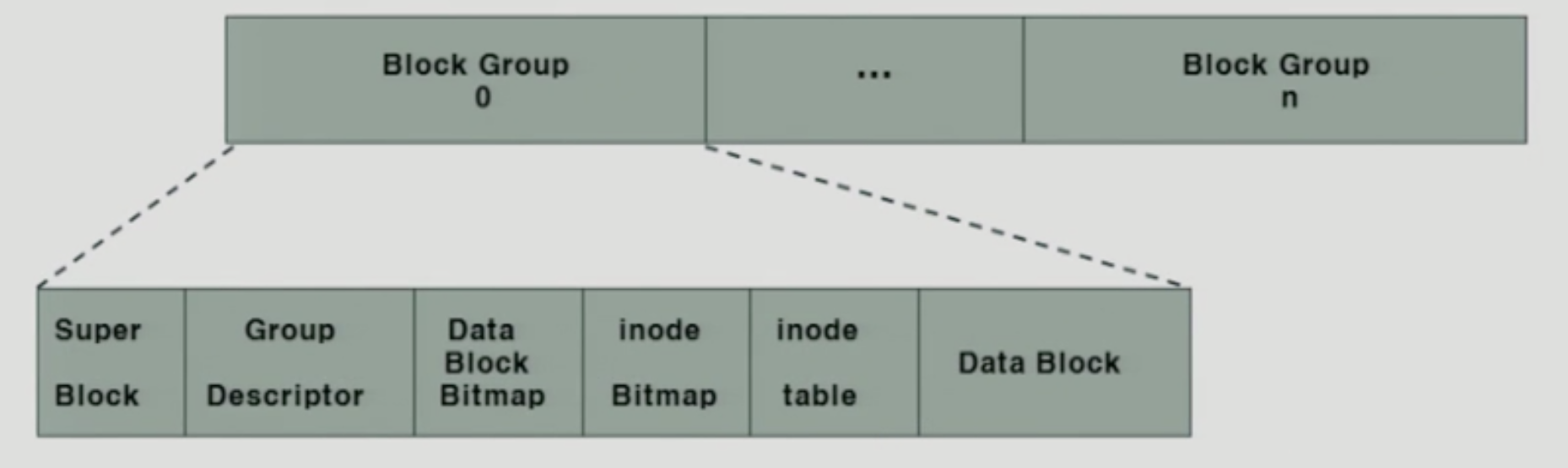
기존의 유닉스 파일 시스템에 비해 개선된 점이,
블록을 그룹화 한다는 점.
각 그룹에 메타데이터와 실제 데이터가 같이 위치함. -> 디스크 탐색 시간 감소

각 그룹마다 동일한 수퍼블록을 중복 저장. -> 디스크 오류에 대비.

수퍼블록
아이노드 수, 가용 아이노드 수, 데이터 블록 수, 가용 데이터 블록 수 등.
그롭당 블록 수, 시간 정보

그룹 디스크립터
데이터 블록 비트맵의 시작 위치, 아이노드 비트맵의 시작위치
첫번재 아이노드의 시작주소, 가용 아이노드 수

데이터 블록 비트맵: 사용중인 데이터블록과 빈 데이터블록의 표시
아이노드 비트맵 : 사용중인 아이노드와 빈 아이노드 표시
아이노드 테이블 : 실제 아이노드의 저장 위치.

전체 파일시스템을 그룹화하여 나눠둔 것이 주요한 포인트

Ext2가 Ext3, Ext4로 발전해왔다.
구조 자체는 거의 동일하나, 큰 차이는 저널링 기능이 추가되었다는 점이다.

저널링이 뭐냐

파일시스템에 잇는걸 작업하기 위해선 메인 메모리의 버퍼캐시에 올려놓고 작업을 함.
전원이 나갓을 때 디램은 내용이 휘발되나, 파일시스템은 비휘발.

버퍼캐시에 있는 데이터가 수정되고, 수정된 내용이 파일시스템에 모두 반영되긴 전에 전원이 나가버리면, 데이터가 훼손되어버림. 아예 아무것도 반영이 안되엇으면 다행인데 반영되는 중간에 크래쉬가 발생하면 문제가 됨.
-> 파일 시스템의 일관성 훼손 문제(inconsistency)

현대 파일 시스템은 이 문제를 해결하기 위해 저널링을 사용.
저널링: 5~30초 단위로 버퍼캐시에 수정된 내용을 디스크 상의 저널영역에 기록
체크포인팅: 수정된 내용을 파일 시스템의 원래 위치에 반영

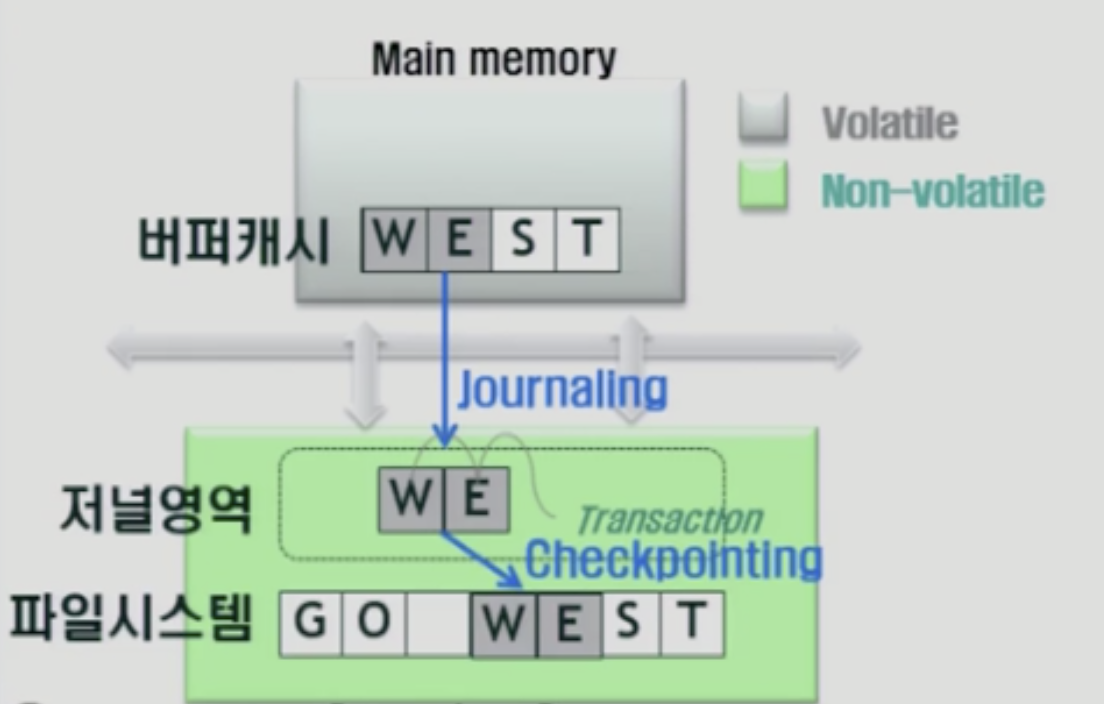
저널링에는 두가지 방법이 있는데, 메타데이터만 저널링하는 방법과 메타데이터와 일반 데이터 모두를 저널링하는 방법이 있음.

저널링 주기가 도래하면 데이터를 파일시스템에 저장한 후 메타데이터를 저널영역에 기록.
체크포인팅 주기가 도래하면 메타데이터를 파일시스템에 반영
크래쉬 발생 시 파일시스템 자체가 깨어지는것 방지 (일부 데이터 훼손가능)

하지만 일반데이터에 대해서는 덮어쓰기 도중 크래쉬가 날 수 있다.
메타데이터만 저널링하면, 파일시스템의 구조 자체가 꺠지는 것은 방지가능하나, 파일 하나하나는 깨어질 수도 있다.

신뢰성이 대단히 높아야한다면 후자로 저널링 모들를 설정함.
저널링 주기가 도래하면 데이터와 메타데이터를 저널영역에 기록.
체크포인팅 주기가 도래하면 데이터와 메타데이터를 팡리시스템에 반영
크래쉬 발생 시 데이터 자체의 복구 보장.

저널링 <- 의미 단위로 업데이트가 되든지, 안되든지임.

---

파일시스템을 위한 버퍼캐시 알고리즘

LRU, LFU 시대가 어떻게 변천되어 왔는가.

버퍼캐시 공간이 파일블록들로 모두 차게 되면, 특정 블록을 제거하고 버퍼캐시에 해당 블록 값을 넣어야한다.
LRU: 가장 오래 전에 사용된 블록 삭제.
LFU: 사용 횟수가 가장 적은 블록 삭제.

각 알고리즘들은 약점들을 가지고 있었다.

LRFU 알고리즘

현재 시점을 기준으로 블록들의 가치를 평가하여 가장 낮은 가치의 블록을 삭제

이 알고리즘은 LFU적인 성질과 LRU적인 성질을 모두 가진다.
최근 참조일수록 블록의 가치 평가에 대한 기여도가 큼.
또한 과거의 모든 참조기록이 현재 시점의 블록 가치계산에 합산됨.

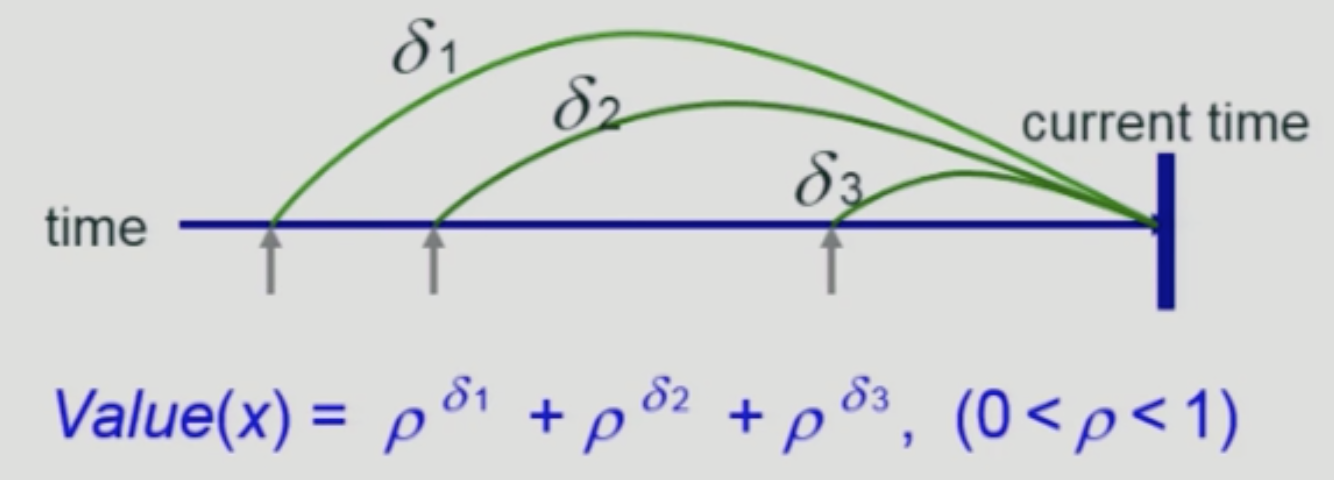
델타 값이 작을수록 높은 가치를 평가받음.

실효성

Space overhead: 만약 어떤 블록이 버퍼캐시에 백만번 쓰이면 각 사용한 시점을 보유하고 있어야하는데, 이에 대한 공간이 소요되는 것이 문제.

Time overhead: 최소한 O(log n) 내에 결정되어야하는데, 매번 어떤 블록을 쫓아낼지 결정하기 위해 버퍼캐시 내 모든 블럭에 대한 밸류를 계산해봐야해서 O(n). 다소 비효율적.

공간 오버헤드 해소

• 특정 시점 t의 가치값이 있다면, t'에서의 가치는 바로 계산될 수 있음.
• 가장 최근에 계산된 밸류값과 시간을 통해 블록당 공간 복잡도를 O(1)로 계산

시간 오버헤드 해소

최소 힙 이용해서 LRFU를 효율적으로 구현할 수 있다.
-> time complexity O(log2 n);