
※ 읽기에 앞서
본 시리즈는 개발자를 희망하지만 코딩테스트에 고통받는
대한민국의 모든 개발자 지망생들을 위해 작성되었습니다.코딩테스트는 전략적으로 접근해야합니다.
개발자를 희망하는 많은 이들이 처음 코딩테스트를 준비할 때,
막연히 문제 풀이를 많이 시도하거나, 단순히 문제집을 참고하는 경우가 많습니다.
최대한 많은 문제를 풀거나, 문제집을 참고하는 것이 틀린 방법은 아니지만 매우 비효율적입니다.
같은 유형의 문제를 풀어도 항상 새롭게 보이고, 시간도 얼마나 걸릴지 장담할 수 없습니다.
문제 유형을 체계적으로 분류하고, 각 유형에 맞는 풀이 방법을 익히는 것이
최소한의 노력으로 최대한의 결과를 얻을 수 있는 가장 효율적인 방법입니다.해당 시리즈의 목표와 전략은 다음과 같습니다.
코딩테스트를 통과하기 위한 전략에 초점을 맞추고 있습니다.
1. 코딩테스트를 만점받기 위한 시리즈가 아닙니다.
2. 모든 유형의 문제를 완벽하게 정복하려 하지 않습니다.
3. 시험에 자주 나오는 유형의 문제만을 완벽히 정복합니다.
4. 코딩테스트를 통과할 수 있을 정도의 점수만을 목표로 합니다.
5. 실제 시험에서 풀 수 있는 문제와 없는 문제를 명확히 구분합니다.
셀 수 없이 많은 모든 유형의 문제를 완벽하게 정복할 수 없을 뿐더러,
프로젝트에서 하드코딩으로 알고리즘을 구현하여 사용하는 경우도 드물고,
애초에 누군가 이러한 알고리즘을 적용하여 만든 라이브러리가 많기 때문입니다.📌 BFS 너비우선탐색
시험에 자주 등장하는 BFS(Breadth First Search) 문제 유형은
기본순회,최단경로,연결요소,플러드필4종류로 구분됩니다.
기본 순회 문제: 현재 노드를 기준으로 이동할 수 있는 모든 노드를 탐색하는 문제최단 경로 문제: 특정 두 노드 사이의 최단 경로를 탐색하는 문제연결 요소 문제: 현재 노드를 기준으로 연결된 모든 노드를 탐색하는 문제플러드 필 문제: 그래프의 영역을 특정 색상으로 채우는 문제, 일명 땅따먹기 문제
이 외에도 `위상 정렬`, `이분 그래프`, `최소신장트리` 등의 유형도 있으나,
위상 정렬과 이분 그래프의 경우, 시험에 잘 등장하지 않는 유형입니다.최소신장트리의 경우,`Kruskal Algorithm`이나 `Prim Algorithm` 등의
별도의 풀이 방법이 있기 때문에 `트리(Tree)` 유형에서 다루도록 하겠습니다.만약 실제 시험에서 이와 같은 유형이 출제된다면, 과감하게 포기하고
전략적으로 풀 수 있는 다른 문제를 찾아 집중하는 것이
코딩테스트를 통과할 확률이 더 높습니다.📌 BFS 기본형태
가장 기본적인 형태의
BFS공식입니다.
Graph는Dictionary,2D Array2가지로 제공됩니다.
📖 Graph Dictionary
Graph가Dictionary일 때,BFS기본공식입니다.
from collections import deque
def bfs(start_node, graph):
queue = deque([start_node])
visited = set([start_node])
while queue:
curr_node = queue.popleft()
for next_node in graph[curr_node]:
if next_node not in visited:
visited.add(next_node)
queue.append(next_node)
return -1def solution():
graph = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F'],
'D': [],
'E': ['F'],
'F': []
}📖 Graph 2D Array
Graph가2D Array일 때,BFS기본공식입니다.
from collections import deque
def bfs(start_x, start_y, graph):
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
queue = deque([(start_x, start_y)])
visited = set([(start_x, start_y)])
while queue:
x, y = queue.popleft()
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < len(graph) and 0 <= ny < len(graph[0]):
if (nx, ny) not in visited:
visited.add((nx, ny))
queue.append((nx, ny))
return -1def solution():
graph = [
['O', 'O', 'O', 'O', 'O', 'X'],
['O', 'O', 'O', 'O', 'X', 'O'],
['O', 'O', 'O', 'X', 'O', 'O'],
['O', 'O', 'X', 'O', 'O', 'O'],
['X', 'O', 'O', 'O', 'O', 'O'],
]📌 BFS 응용형태
다양한 응용 형태의
BFS공식입니다.
기본형태에 특정조건을 추가하는 것이 중요한 유형입니다.
📘 응용① 기본순회
📖 Graph Dictionary
기본형태에서 크게 벗어나지 않지만 추가조건이 제시됩니다.
응용 포인트1: 문제에서 특정 종료 조건을 제시하는 경우 사용합니다.
응용 포인트2: 문제에서 특정 이동 조건을 제시하는 경우 사용합니다.
def bfs(start_node, graph):
queue = deque([start_node])
visited = set([start_node])
while queue:
curr_node = queue.popleft()
# 응용 포인트1: 문제에서 제시하는 종료 조건
if curr_node == 'T':
return curr_node
for next_node in graph[curr_node]:
if next_node not in visited:
# 응용 포인트2: 문제에서 제시하는 추가 이동 조건
if next_node != 'X':
visited.add(next_node)
queue.append(next_node)
return -1def solution():
graph = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F'],
'D': [],
'E': ['F'],
'F': []
}📖 Graph 2D Array
기본형태에서 크게 벗어나지 않지만 추가조건이 제시됩니다.
응용 포인트1: 문제에서 특정 종료 조건을 제시하는 경우 사용합니다.
응용 포인트2: 문제에서 특정 이동 조건을 제시하는 경우 사용합니다.
from collections import deque
def bfs(start_row, start_col, graph):
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
rows, cols = len(graph), len(graph[0])
queue = deque([(start_row, start_col)])
visited = set([(start_row, start_col)])
while queue:
row, col = queue.popleft()
# 응용 포인트1: 문제에서 제시하는 종료 조건
if row == 'T' and col == 'T':
return row, col
for i in range(4):
next_row = row + dx[i]
next_col = col + dy[i]
if 0 <= next_row < rows and 0 <= next_col < cols:
if (next_row, next_col) not in visited:
# 응용 포인트2: 문제에서 제시하는 추가 이동 조건
if graph[next_row][next_col] != 'X':
visited.add((next_row, next_col))
queue.append((next_row, next_col))
return -1def solution():
graph = [
['O', 'O', 'O', 'O', 'O', 'X'],
['O', 'O', 'O', 'O', 'X', 'O'],
['O', 'O', 'O', 'X', 'O', 'O'],
['O', 'O', 'X', 'O', 'O', 'O'],
['X', 'O', 'O', 'O', 'O', 'O'],
]📘 응용② 최단경로, 최단거리
📖 Graph Dictionary, 최단경로
최단경로를 찾는
BFS공식입니다.
응용 포인트1: 문제에서 특정 결과 값을 요구하는 경우 사용합니다.
응용 포인트2: 문제에서 특정 종료 조건을 제시하는 경우 사용합니다.
from collections import deque
def bfs_shortest_path(start_node, end_node, graph):
# 응용 포인트1: {노드: [경로]}
queue = deque([start_node])
visited = set([start_node])
path = {start_node: [start_node]}
while queue:
curr_node = queue.popleft()
# 응용 포인트2: 문제에서 제시하는 종료 조건
if curr_node == end_node:
return path[curr_node]
for next_node in graph[curr_node]:
if next_node not in visited:
visited.add(next_node)
queue.append(next_node)
# 응용 포인트1: {다음노드: [현재경로] + [다음경로]}
path[next_node] = path[curr_node] + [next_node]
return -1📖 Graph Dictionary, 최단거리
최단거리를 찾는
BFS공식입니다.
응용 포인트1: 문제에서 특정 결과 값을 요구하는 경우 사용합니다.
응용 포인트2: 문제에서 특정 종료 조건을 제시하는 경우 사용합니다.
from collections import deque
def bfs_shortest_distance(start_node, end_node, graph):
# 응용 포인트1: {노드: 거리}
queue = deque([start_node])
visited = set([start_node])
dist = {start_node: 0}
while queue:
curr_node = queue.popleft()
# 응용 포인트2: 문제에서 제시하는 종료 조건
if curr_node == end_node:
return dist[curr_node]
for next_node in graph[curr_node]:
if next_node not in visited:
visited.add(next_node)
queue.append(next_node)
# 응용 포인트1: {다음노드: 현재거리 + 1}
dist[next_node] = dist[curr_node] + 1
return -1📖 Graph 2D Array, 최단경로
최단경로를 찾는
BFS공식입니다.
응용 포인트1: 문제에서 특정 결과 값을 요구하는 경우 사용합니다.
응용 포인트2: 문제에서 특정 종료 조건을 제시하는 경우 사용합니다.
응용 포인트3: 문제에서 특정 이동 조건을 제시하는 경우 사용합니다.
from collections import deque
def BFS(start_x, start_y, end_x, end_y, graph):
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
n, m = len(graph), len(graph[0])
# 응용 포인트1: (좌표x, 좌표y, [경로])
visited = set([(start_x, start_y)])
queue = deque([(start_x, start_y, [(start_x, start_y)])])
while queue:
x, y, path = queue.popleft()
# 응용 포인트2: 문제에서 제시하는 종료 조건
if x == end_x and y == end_y:
return path
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < n and 0 <= ny < m:
if (nx, ny) not in visited:
# 응용 포인트3: 문제에서 제시하는 추가 이동 조건
if graph[nx][ny] == 1:
# 응용 포인트1: (다음좌표x, 다음좌표y, [현재경로] + [다음좌표])
visited.add((nx, ny))
queue.append((nx, ny, path + [(nx, ny)]))
return -1📖 Graph 2D Array, 최단거리
최단거리를 찾는
BFS공식입니다.
응용 포인트1: 문제에서 특정 결과 값을 요구하는 경우 사용합니다.
응용 포인트2: 문제에서 특정 종료 조건을 제시하는 경우 사용합니다.
응용 포인트3: 문제에서 특정 이동 조건을 제시하는 경우 사용합니다.
from collections import deque
def BFS(start_x, start_y, end_x, end_y, graph):
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
n, m = len(graph), len(graph[0])
# 응용 포인트1: (좌표x, 좌표y, 거리)
visited = set([(start_x, start_y)])
queue = deque([(start_x, start_y, 1)])
while queue:
x, y, dist = queue.popleft()
# 응용 포인트2: 문제에서 제시하는 종료 조건
if x == end_x and y == end_y:
return dist
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < n and 0 <= ny < m:
if (nx, ny) not in visited:
# 응용 포인트3: 문제에서 제시하는 추가 이동 조건
if graph[nx][ny] == 1:
# 응용 포인트1: (다음좌표x, 다음좌표y, 현재거리 + 1)
visited.add((nx, ny))
queue.append((nx, ny, dist + 1))
return -1📖 Graph Dictionary, 최단경로, 최단거리
최단경로와 최단거리를 모두 찾는
BFS공식입니다.
응용 포인트1: 문제에서 특정 결과 값을 요구하는 경우 사용합니다.
응용 포인트2: 최단경로의 길이를 통해 최단거리도 함께 반환합니다.
응용 포인트3: 문제에서 특정 종료 조건을 제시하는 경우 사용합니다.
from collections import deque
def BFS(start_node, end_node, graph):
# 응용 포인트1: {노드: [경로]}
queue = deque([start_node])
visited = set([start_node])
path = {start_node: [start_node]}
while queue:
curr_node = queue.popleft()
# 응용 포인트2, 3: 최단경로의 길이를 통한 최단거리
if curr_node == end_node:
return path[curr_node], len(path[curr_node]) - 1
for next_node in graph[curr_node]:
if next_node not in visited:
visited.add(next_node)
queue.append(next_node)
# 응용 포인트1: {다음노드: [현재경로] + [다음경로]}
path[next_node] = path[curr_node] + [next_node]
return [], -1📖 Graph 2D Array, 최단경로, 최단거리
최단경로와 최단거리를 모두 찾는
BFS공식입니다.
응용 포인트1: 문제에서 특정 결과 값을 요구하는 경우 사용합니다.
응용 포인트2: 최단경로의 길이를 통해 최단거리도 함께 반환합니다.
응용 포인트3: 문제에서 특정 종료 조건을 제시하는 경우 사용합니다.
응용 포인트4: 문제에서 특정 이동 조건을 제시하는 경우 사용합니다.
from collections import deque
def BFS(start_x, start_y, end_x, end_y, graph):
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
n, m = len(graph), len(graph[0])
# 응용 포인트1: (좌표x, 좌표y, [경로])
visited = set([(start_x, start_y)])
queue = deque([(start_x, start_y, [(start_x, start_y)])])
while queue:
x, y, path = queue.popleft()
# 응용 포인트2, 3: 최단경로의 길이를 통한 최단거리
if x == end_x and y == end_y:
return path, len(path) - 1
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < n and 0 <= ny < m:
if (nx, ny) not in visited:
# 응용 포인트4: 문제에서 제시하는 추가 이동 조건
if graph[nx][ny] == 1:
# 응용 포인트1: (다음좌표x, 다음좌표y, [현재경로] + [다음좌표])
visited.add((nx, ny))
queue.append((nx, ny, path + [(nx, ny)]))
return [], -1📘 응용③ - 연결요소
📖 Graph Dictionary
특정노드를 기준으로 연결된 모든 요소를 찾는
BFS공식입니다.
응용 포인트1: 첫 노드를 방문하지 않은 것으로 처리해야 합니다.
응용 포인트2: 특정 노드를 기준으로 연결된 모든 요소를 탐색합니다.
응용 포인트3: 특정 노드를 기준으로 연결된 모든 요소를 결과값에 추가합니다.
from collections import deque
def bfs_connected_components(start_node, graph):
# 응용 포인트1: 첫 노드를 방문하지 않은 것으로 처리
visited = set()
queue = deque([start_node])
connected_components = []
while queue:
base_node = queue.popleft()
# 응용 포인트1: 기준노드
if base_node not in visited:
component = []
visited.add(base_node)
queue.append(base_node)
# 응용 포인트2: 기준노드에 연결된 요소 탐색
while queue:
curr_node = queue.popleft()
component.append(curr_node)
for next_node in graph[curr_node]:
if next_node not in visited:
visited.add(next_node)
queue.append(next_node)
# 응용 표인트3: 각각의 덩어리로 묶인 연결요소
connected_components.append(component)
return connected_components📖 Graph 2D Array
특정노드를 기준으로 연결된 모든 요소를 찾는
BFS공식입니다.
응용 포인트1:visited를bfs()가 아닌solution()에서 생성합니다.
응용 포인트2: 특정 노드를 기준으로 연결된 모든 요소를 탐색합니다.
응용 포인트3: 문제에서 특정 이동 조건을 제시하는 경우 사용합니다.
응용 포인트4: 모든 노드를 순회하며 특정 노드의 기준점을 잡습니다.
응용 포인트5:solution()에서도 이동조건을 검사하며,bfs()결과를 최종 결과에 추가합니다.
from collections import deque
# 응용 포인트1: solution()에게 visited를 받아 처리
def bfs(start_x, start_y, graph, visited):
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
n, m = len(graph), len(graph[0])
visited[start_x][start_y] = True
component = []
queue = deque([(start_x, start_y)])
while queue:
x, y = queue.popleft()
component.append((x, y)) # 응용 포인트2: 기준노드에 연결된 요소 탐색
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
# 응용 포인트3: 추가 이동 조건 graph[nx][ny]
if 0 <= nx < n and 0 <= ny < m:
if graph[nx][ny] and not visited[nx][ny]:
visited[nx][ny] = True
queue.append((nx, ny))
return componentdef solution(graph):
# 응용 포인트1: bfs()에게 넘겨줄 visited 생성
n, m = len(graph), len(graph[0])
visited = [[False] * m for _ in range(n)]
# 응용 포인트4: 모든 노드를 순회하며, 각각의 모든 연결요소 탐색
answer = []
for i in range(n):
for j in range(m):
# 응용 포인트5: 중복되지 않도록 solution()에서 이동 조건 검사
if graph[i][j] and not visited[i][j]:
answer.append(bfs(i, j, graph, visited))
return answer📘 응용④ - 플러드 필
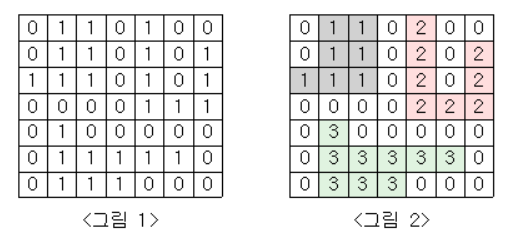
위와 같은 일종의 땅따먹기 형태의 문제에서 사용되는
BFS공식입니다.
📖 Graph Dictionary
연결요소들의 집합을 다른 색으로 구분하는
BFS공식입니다.
이러한 땅따먹기 유형의 문제는 보통 그래프를2D Array로 제공합니다.
연결요소의 연장선상의 문제로,solution()에서 모두 순회하며 다른 집합도 찾습니다.
응용 포인트1: 첫 노드(기준 노드)는 방문처리하지 않습니다.
응용 포인트2:extend()를 통해for next_node in graph[curr_node]:생략
from collections import deque
def bfs_connected_components(start, graph):
# 응용 포인트1: 첫 노드는 방문처리하지 않음
visited = set()
queue = deque([start])
connected_component = []
while queue:
curr_node = queue.popleft()
# 응용 포인트2: extend로 for next_node 생략
if curr_node not in visited:
visited.add(curr_node)
queue.extend(graph[curr_node])
connected_component.append(curr_node)
return connected_component📖 Graph 2D Array
연결요소들의 집합을 다른 색으로 구분하는
BFS공식입니다.
연결요소의 연장선상의 문제로,solution()에서 모두 순회하며 다른 집합도 찾습니다.
응용 포인트1: 연결요소인지 확인할 기준색을 추출하고 비교합니다.
응용 포인트2: 연결요소인 경우 다른 연결요소집합과 구분할 수 있도록 새로운 색으로 변경합니다.
from collections import deque
def bfs_flood_fill(sx, sy, graph, new_color):
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
# 응용 포인트1: 기준이 될 색깔을 추출
queue = deque([(sx, sy)])
visited = set([(sx, sy)])
base_color = graph[sx][sy]
while queue:
# 응용 포인트2: 새로운 하나의 색으로 변경
x, y = queue.popleft()
graph[x][y] = new_color
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
# 응용 포인트1: 시작노드의 색깔과 같은지 검사
if 0 <= nx < len(graph) and 0 <= ny < len(graph[0]):
if (nx, ny) not in visited and graph[nx][ny] == base_color:
visited.add((nx, ny))
queue.append((nx, ny))
return graph
정리 너무 잘해놓으셧네요.. 좋아요 박고갑니다