레드 블랙 트리

balanced tree..?

CFS에서 레드 블랙 트리를 통해 프로세스를 관리하여 탐색시간을 줄인다.
binary search tree를 사용하면 탐색 시 O(logN)의 시간복잡도를 가진다.

하지만..
만약 트리가 편향된다면 어떻게 될까?

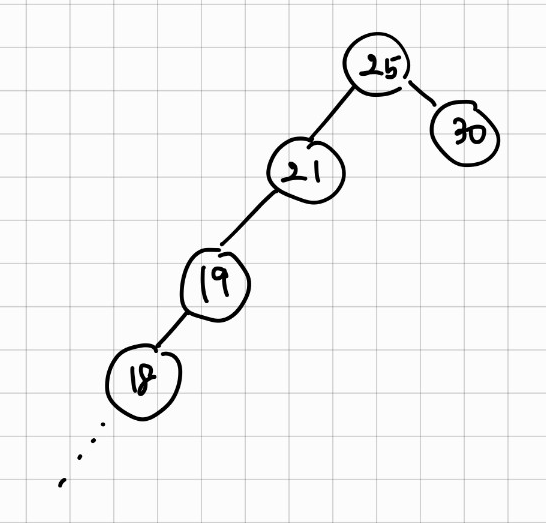
binary search tree가 편향된다면, 원소를 찾을 때, O(N)의 시간복잡도를 가지게 된다. 이럴 경우, binary search tree를 유지할 필요가 없다!!
=> 이를 보완하기 위해 자동으로 균형을 맞춰주는 balanced tree가 등장했고, 그 중 하나가 red-black tree다.

레드 블랙 트리

기본 규칙

1. 레드 블랙 트리는 트리의 노드를 빨간색 또는 검은색으로 칠한다
2. 루트 노드는 검은색이다
3. NIL(리프 노드)은 검은색으로 취급
4. 빨간색 노드의 자식들은 검은색 노드다.
5. 루트 노드에서 모든 리프 노드로 갈 때 거쳐가는 검은색 노드의 수는 같다

위 규칙을 수행하면 높이를 제한할 수 있나?

b(x) = x부터 NIL까지 갈 때 거쳐가는 black node의 수 (x 미포함, NIL포함)

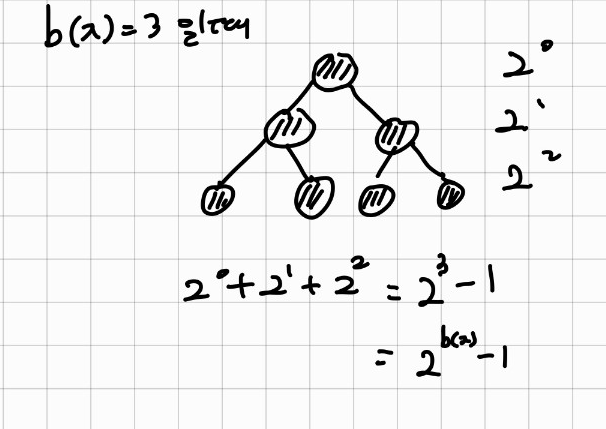
서브 트리가 모두 black 노드일 때가 서브 트리의 노드 수가 최소가 될 때이다!!

x를 루트로 하는 서브 트리의 노드 개수를 n(x)이라고 하자.
n(x) >= 2^(b(x)) -1 를 만족한다.
b(root) >= height/2를 만족한다.
(기본 규칙 4번과 5번때문에.. ex) b(root) == 3이면, 높이의 최대는 red와 black을 번갈아 가면서 배치한 6이다!)

위 두 식을 합하면 n(root) + 1 >= 2^(height/2)이 되고, 이 양 변에 로그를 씌우면
height <= 2*log(n(root)+1) 가 된다.

따라서 red-black 트리에서 원소를 탐색할 때 걸리는 시간은 O(logN)이다!!

새로운 노드가 들어오면?

새로운 노드를 그대로 추가하면, red-black tree의 기본 규칙에 위배될 수가 있다!
단순히 노드를 추가하는 것이 아니라, 추가적인 동작이 필요하다!

새로운 노드를 삽입할 때는 red 노드를 삽입한다. 그리고 기본 규칙에 위배될 경우, 다음 2가지 방식 중 하나를 수행한다.
어떤 동작을 수행할지는 uncle node(부모의 형제 node)를 확인한다!

Reconstructing

• uncle node가 black node일 때
• 방법
  1. 삽입된 노드, 부모 노드, 조부모 노드를 정렬한다.
  2. 가운데 값을 부모 노드로 만들고, 다른 두 노드를 자식 노드로 만든다.
  부모 노드는 black node, 자식 노드는 red node로
  3. 이후 아래에 다른 노드들을 이어준다.

Repainting

• uncle node가 red node일 때
• 방법
  1. 부모와 삼촌을 black node로 만든다.
  2. 조부모를 red node로 만든다.
  3. 조부모를 red node로 만들었을 때, 규칙 4가 위배될 수 있다.
  4. 이 경우 조부모 node를 삽입된 node라고 생각하고, 과정을 재귀적으로 진행
  

평소에 red-black tree에 대한 막연한 개념만 가지고 있었는데, 어떻게 red-black tree가 balanced하게 유지될 수 있는지에 대해서 구체적으로 알게 되었다.